大厂秋招真题【BFS+DP】华为20230921秋招T3-PCB印刷电路板布线【欧弟算法】全网最全大厂秋招题解

news2024/12/25 0:18:02

题目描述与示例

题目描述

在PCB印刷电路板设计中，器件之间的连线，要避免线路的阻抗值增大，而且器件之间还有别的器任和别的干扰源，在布线时我们希望受到的干扰尽量小。

现将电路板简化成一个M × N的矩阵，每个位置（单元格）的值表示其源干扰度。

如果单元格的值为0，表示此位置没有干扰源，如果单元格的值为非0，则表示此位置是干扰源，其值为源干扰度。连线经过干扰源或干扰源附近会增加连线的总干扰度。

位置A[x,y]的干扰源的源干扰广为d (d>0)，则连线的干扰度计算如下：

1、若连线经过位置A[x,y]，则其总开扰广会增加加

2、若连线经过离位置A[x,y]距离小于d的位置时，设其距离为k，则总干扰度会增加(d-k)

3、若连线经过离位置A[x,y]距离大于或等于d的位置时，总干扰都不会增加；

注：位置[x1,y1]和位置[x2,y2]之间距离的定义为：|x1-x2|+|y1-y2|。

如下3x3矩阵，位置[1,1]的源干扰度是2，连线的位置序列为：[0,0]->[0,1]->[0,2]->[1,2]->[2,2]。

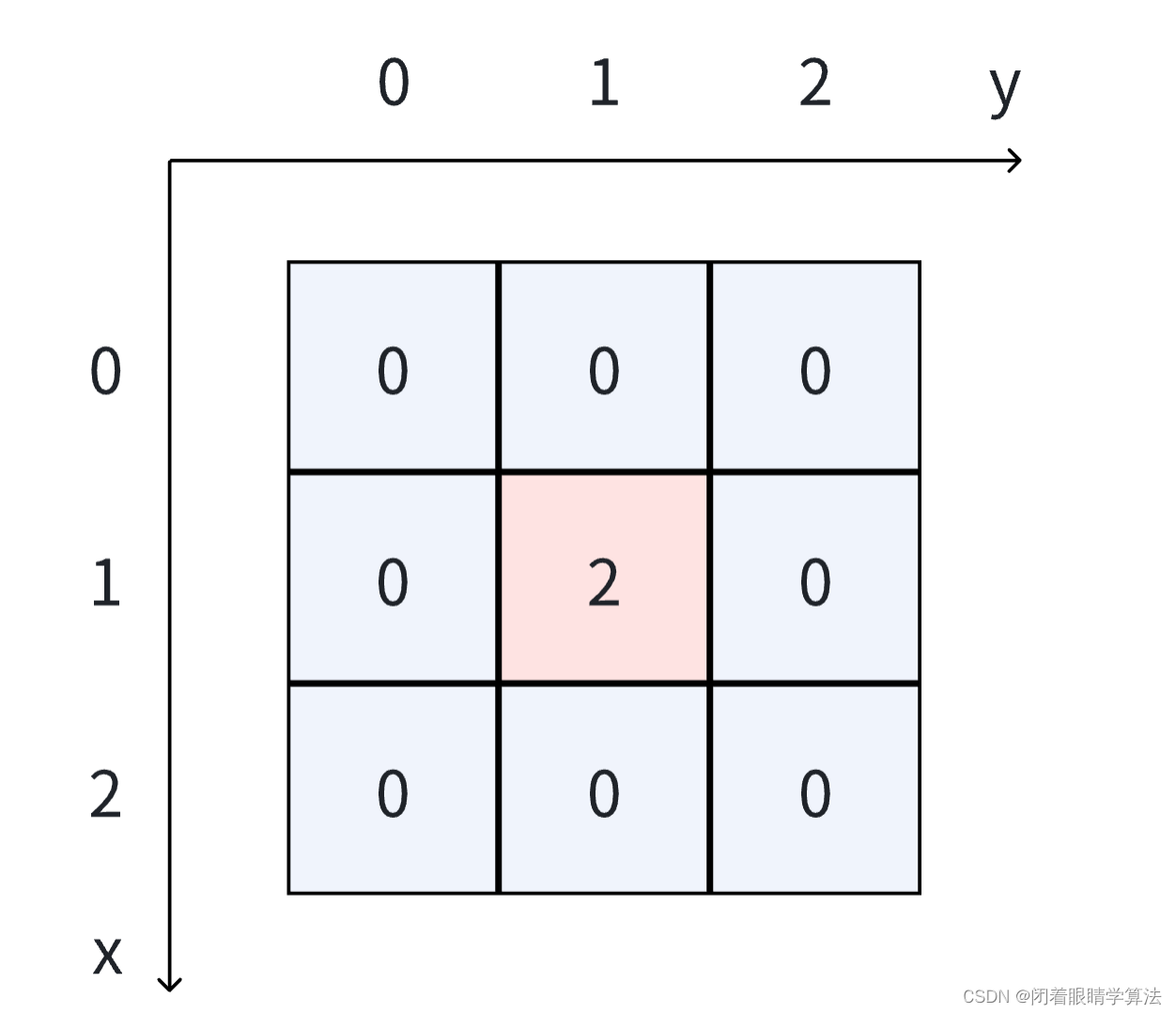
其中[0,1]和[1,0]到干扰源的距离为1，会叠加1的干扰度；其他位置到[1,1]的距离均大于等于2，所以不会叠加干扰度。因此这条连线的总干扰度为2。

现在我们需要将左上角的器件到右下角的器件进行连线，两个器件的位置分别是左上角的[0,0]和右下角的[M-1,N-1]。由于我们希望连线尽量地短，从位置[0,0]到[M-1,N-1]的连线途中，我们规定连线只能向下或向右。

请根据输入(M × N的矩阵)，计算出连线的最小干扰度。

输入描述

第一行是两个整数M和N(M和N最大值为1000)，表示行数和列数；

接着是M行的数据，每一包含N个整数，代表每个位置的源干扰度，每个源干扰度小于50。

输出描述

左上角[0,0]到右下角[M-1,N-1]连线的最小总干扰度。

示例一

输入

3 3
0 0 0
0 2 0
0 0 0

输出

2

说明

其中一条可以使干扰度最小的路径为：[0,0]->[0,1]->[0,2]->[1,2]->[2,2]，其干扰度为2。

示例二

输入

5 5
0 0 0 0 0
0 0 2 0 0
0 2 0 2 0
0 0 0 0 0
0 0 0 0 0

输出

1

说明

先从[0,0]往下走到最下面[4,0]，再往石走到右下角[4,4]，途径[2,0]时叠加一个干扰度。

示例三

输入

5 5
0 0 0 0 0
0 0 2 0 0
0 2 0 2 0
0 0 2 0 0
0 0 0 0 0

输出

2

时空限制

时间限制： C/C++ 2000MS，其他语言4000MS

内存限制： C/C++ 256MB，其他语言512MB

解题思路

本题属于综合性较强的题目，结合了BFS和DP两个知识点。

首先我们需要根据原矩阵，构建出每一个位置干扰值叠加的结果，得到一个新的矩阵grid_new。这里显然就是一个基于BFS计算层数的问题。

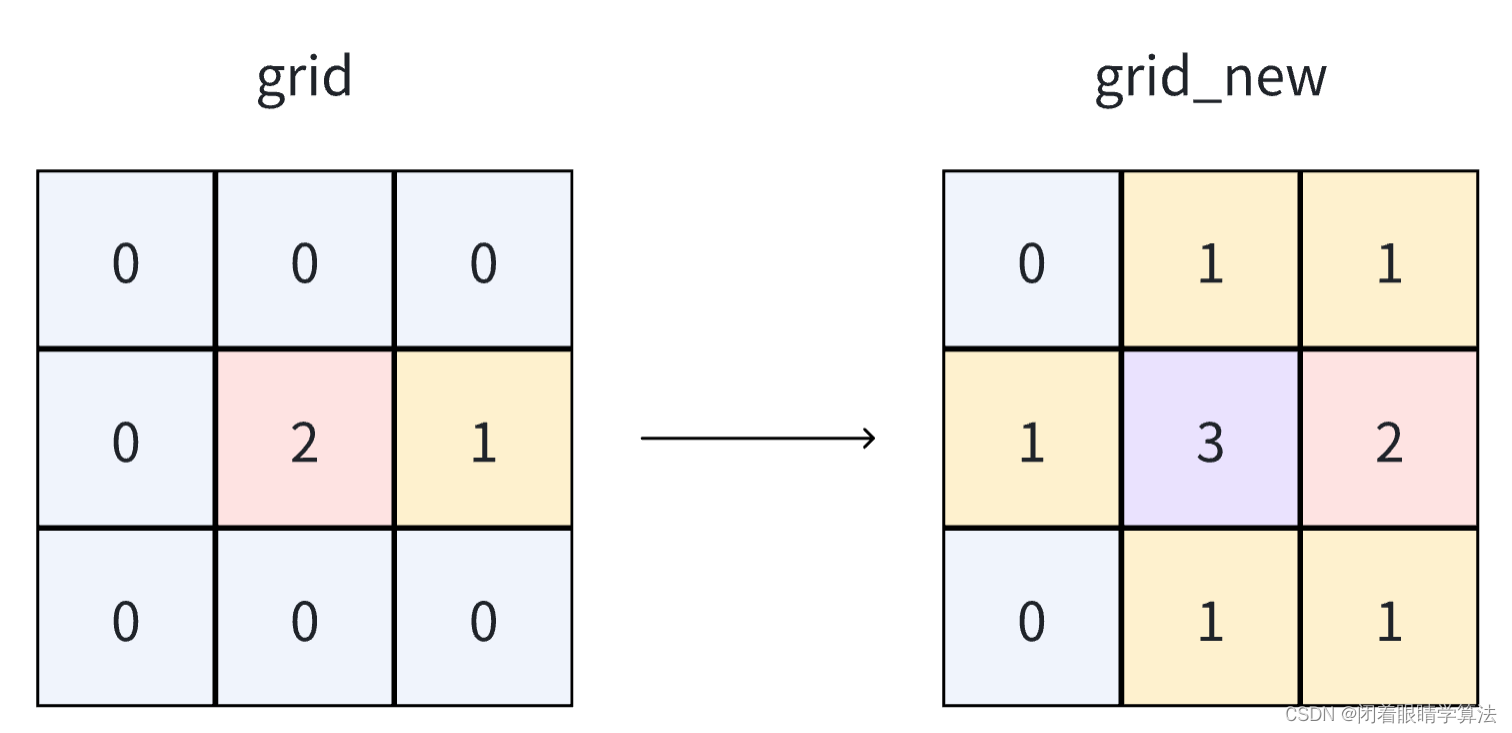
在这里插入图片描述

在得到新的矩阵grid_new之后，问题就转变为，对grid_new构建一条从左上到右下的路径，每次只能够向右或向下移动，路径经过的点的总和需要最小。这是一个经典的路径DP问题，和LeetCode64、最小路径和完全一致。

代码

Python

# 题目：【DP】华为2023秋招-PCB印刷电路板布线
# 作者：闭着眼睛学数理化
# 算法：DP/BFS
# 代码有看不懂的地方请直接在群上提问


from collections import deque


DIRECTIONS = [(0, 1), (1, 0), (0, -1), (-1, 0)]


# 对于grid中每一个干扰源，以干扰源作为起点进行BFS，更新grid_new
def BFS_update_grid_new(val, grid_new, i, j, m, n):
    check_list = [[0] * n for _ in range(m)]
    check_list[i][j] = 1
    grid_new[i][j] += val
    q = deque()
    q.append((i, j))
    # 注意这里退出循环的条件和val相关
    while val > 1:
        val -= 1
        qSize = len(q)
        for _ in range(qSize):
            cur_x, cur_y = q.popleft()
            for dx, dy in DIRECTIONS:
                nxt_x, nxt_y = cur_x+dx, cur_y+dy
                if 0 <= nxt_x < m and 0 <= nxt_y < n and check_list[nxt_x][nxt_y] == 0:
                    q.append((nxt_x, nxt_y))
                    grid_new[nxt_x][nxt_y] += val
                    check_list[nxt_x][nxt_y] = 1


# 用于解决最小路径和问题的函数
def find_min_sum_path(grid_new, m, n):
    # 构建大小为m*n的dp数组，dp[i][j]表示
    # 到达grid_new中的点(i,j)，所需的最小路径和
    dp = [[0] * (n) for _ in range(m)]
    # 初始化(0,0)位置
    dp[0][0] = grid_new[0][0]
    # 初始化dp数组第0行，只能从左边向右转移得到
    for j in range(1, n):
        dp[0][j] += dp[0][j-1] + grid_new[0][j]
    # 初始化dp数组第0列，只能从上边向下转移得到
    for i in range(1, m):
        dp[i][0] += dp[i-1][0] + grid_new[i][0]
    # 遍历剩余所有点
    # 点(i,j)的状态，只能从点(i-1,j)向下或者从点(i,j-1)向右转移得到
    # 故动态转移方程为dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid_new[i][j]
    for i in range(1, m):
        for j in range(1, n):
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid_new[i][j]

    return dp[-1][-1]


# 输入行数m，列数n
m, n = map(int, input().split())
# 构建原干扰值矩阵
grid = list()
for _ in range(m):
    grid.append(list(map(int, input().split())))

# 初始化干扰值叠加后的新矩阵gird_new
grid_new = [[0] * n for _ in range(m)]

for i in range(m):
    for j in range(n):
        # 对于每一个干扰源，使用BFS更新grid_new
        if grid[i][j] != 0:
            val = grid[i][j]
            BFS_update_grid_new(val, grid_new, i, j, m, n)

# 调用函数find_min_sum_path，输出答案
print(find_min_sum_path(grid_new, m, n))

Java

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;

public class Main {
    private static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    // Function to perform BFS and update gridNew
    private static void BFSUpdateGridNew(int val, int[][] gridNew, int i, int j, int m, int n) {
        int[][] checkList = new int[m][n];
        checkList[i][j] = 1;
        gridNew[i][j] += val;
        Deque<int[]> queue = new ArrayDeque<>();
        queue.add(new int[]{i, j});

        while (val > 1) {
            val--;
            int qSize = queue.size();
            for (int k = 0; k < qSize; k++) {
                int[] current = queue.poll();
                int curX = current[0];
                int curY = current[1];

                for (int[] dir : DIRECTIONS) {
                    int nextX = curX + dir[0];
                    int nextY = curY + dir[1];
                    if (nextX >= 0 && nextX < m && nextY >= 0 && nextY < n && checkList[nextX][nextY] == 0) {
                        queue.add(new int[]{nextX, nextY});
                        gridNew[nextX][nextY] += val;
                        checkList[nextX][nextY] = 1;
                    }
                }
            }
        }
    }

    // Function to find the minimum sum path
    private static int findMinSumPath(int[][] gridNew, int m, int n) {
        int[][] dp = new int[m][n];
        dp[0][0] = gridNew[0][0];

        for (int i = 1; i < m; i++) {
            dp[i][0] = dp[i - 1][0] + gridNew[i][0];
        }

        for (int j = 1; j < n; j++) {
            dp[0][j] = dp[0][j - 1] + gridNew[0][j];
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + gridNew[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        int[][] grid = new int[m][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                grid[i][j] = sc.nextInt();
            }
        }

        int[][] gridNew = new int[m][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0) {
                    int val = grid[i][j];
                    BFSUpdateGridNew(val, gridNew, i, j, m, n);
                }
            }
        }

        System.out.println(findMinSumPath(gridNew, m, n));
    }
}

C++

#include <iostream>
#include <vector>
#include <deque>
using namespace std;

const vector<pair<int, int>> DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

// Function to perform BFS and update grid_new
void BFSUpdateGridNew(int val, vector<vector<int>>& gridNew, int i, int j, int m, int n) {
    vector<vector<int>> checkList(m, vector<int>(n, 0));
    checkList[i][j] = 1;
    gridNew[i][j] += val;
    deque<pair<int, int>> q;
    q.push_back({i, j});

    while (val > 1) {
        val--;
        int qSize = q.size();
        for (int k = 0; k < qSize; k++) {
            int curX = q.front().first;
            int curY = q.front().second;
            q.pop_front();

            for (const auto& dir : DIRECTIONS) {
                int nextX = curX + dir.first;
                int nextY = curY + dir.second;
                if (nextX >= 0 && nextX < m && nextY >= 0 && nextY < n && checkList[nextX][nextY] == 0) {
                    q.push_back({nextX, nextY});
                    gridNew[nextX][nextY] += val;
                    checkList[nextX][nextY] = 1;
                }
            }
        }
    }
}

// Function to find the minimum sum path
int FindMinSumPath(const vector<vector<int>>& gridNew, int m, int n) {
    vector<vector<int>> dp(m, vector<int>(n, 0));
    dp[0][0] = gridNew[0][0];

    for (int i = 1; i < m; i++) {
        dp[i][0] = dp[i - 1][0] + gridNew[i][0];
    }

    for (int j = 1; j < n; j++) {
        dp[0][j] = dp[0][j - 1] + gridNew[0][j];
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + gridNew[i][j];
        }
    }

    return dp[m - 1][n - 1];
}

int main() {
    int m, n;
    cin >> m >> n;
    vector<vector<int>> grid(m, vector<int>(n));

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            cin >> grid[i][j];
        }
    }

    vector<vector<int>> gridNew(m, vector<int>(n, 0));

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] != 0) {
                int val = grid[i][j];
                BFSUpdateGridNew(val, gridNew, i, j, m, n);
            }
        }
    }

    cout << FindMinSumPath(gridNew, m, n) << endl;

    return 0;
}

时空复杂度

时间复杂度：O(MNk)。其中k为干扰源的数目，一共需要进行k次BFS，每次BFS的时间复杂度为O(MN)。另外，DP过程的时间复杂度为O(MN)。

空间复杂度：O(MN)。grid_new、check_list、dp等二维矩阵所占空间均为O(MN)。

华为OD算法/大厂面试高频题算法练习冲刺训练

  • 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

  • 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

  • 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

  • 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

  • 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

  • 可查看链接 OD算法冲刺训练课程表 & OD真题汇总(持续更新)

  • 绿色聊天软件戳 od1336了解更多

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1044383.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何快速学习AdsPower RPA（1）——简单、进阶部分

如何快速学习AdsPower RPA（1）——简单、进阶部分

你是否刚开始学习使用AdsPower的RPA功能&#xff1f; 你是否对着这些操作选项头皮发麻&#xff0c;不知所措&#xff1f; 你是否想快速学会RPA&#xff1f; 你是否想编写出满足各种业务场景的RPA流程&#xff1f; 以上这些&#xff0c;Tool哥统统都帮你搞定&#xff01; Too…
阅读更多...
科技成果鉴定测试有多重要?可出具专业测试报告的软件测评机构推荐

科技成果鉴定测试有多重要?可出具专业测试报告的软件测评机构推荐

科技成果鉴定测试在现代社会中具有重要意义&#xff0c;它不仅可以评估科技成果的价值和可行性&#xff0c;还可以为科技创新提供决策依据&#xff0c;推动科技进步和社会发展&#xff0c;那么科技成果鉴定测试究竟重要在哪呢? 1、对于科技项目的投资决策至关重要。鉴定测试可…
阅读更多...
YOLOV8-DET转ONNX和RKNN

YOLOV8-DET转ONNX和RKNN

目录 1. 前言 2.环境配置 (1) RK3588开发板Python环境 (2) PC转onnx和rknn的环境 3.PT模型转onnx 4. ONNX模型转RKNN 6.测试结果 1. 前言 yolov8就不介绍了&#xff0c;详细的请见YOLOV8详细对比&#xff0c;本文章注重实际的使用&#xff0c;从拿到yolov8的pt检测模型&…
阅读更多...
玩转gpgpu-sim 04记—— __cudaRegisterBinary() of gpgpu-sim 到底做了什么

玩转gpgpu-sim 04记—— __cudaRegisterBinary() of gpgpu-sim 到底做了什么

官方文档&#xff1a; GPGPU-Sim 3.x Manual __cudaRegisterBinary(void*) 被执行到的代码逻辑如下&#xff1a; void** CUDARTAPI __cudaRegisterFatBinary( void *fatCubin ) { #if (CUDART_VERSION < 2010)printf("GPGPU-Sim PTX: ERROR ** this version of GPGPU…
阅读更多...
查看Linux系统信息的常用命令

查看Linux系统信息的常用命令

文章目录 1. 机器配置查看2. 常用分析工具3. 常用指令解读3.1 lscpu 4. 定位僵尸进程5. 参考 1. 机器配置查看 # 总核数物理CPU个数x每颗物理CPU的核数 # 总逻辑CPU数物理CPU个数x每颗物理CPU的核数x超线程数 cat /proc/cpuinfo| grep "physical id"| sort| uniq| w…
阅读更多...
电子电路学习笔记之NCV6324BMTAATBG——同步降压转换器

电子电路学习笔记之NCV6324BMTAATBG——同步降压转换器

关于同步降压转换器&#xff1f; 是一种广泛应用于各种电子产品中的转换器。它具有输入范围宽、转换效率高、输出电流大等优点。在同步降压型转换器的驱动电路中&#xff0c;一般包括电平移位电路、死区时间控制电路以及过零检测电路等。 电平移位电路用于将固定电平Vcc和GND…
阅读更多...
86、Redis 的 value 所支持的数据类型（String、List、Set、Zset、Hash）----＞String相关命令

86、Redis 的 value 所支持的数据类型（String、List、Set、Zset、Hash）----＞String相关命令

本次讲解要点&#xff1a; String相关命令&#xff1a;String是指value中的数据类型 启动redis服务器&#xff1a; 打开小黑窗&#xff1a; C:\Users\JH>e: E:>cd E:\install\Redis6.0\Redis-x64-6.0.14\bin E:\install\Redis6.0\Redis-x64-6.0.14\bin>redis-server.…
阅读更多...
【知识点随笔分析】我看看谁还不会用CURL命令

【知识点随笔分析】我看看谁还不会用CURL命令

目录 前言&#xff1a; CURL介绍&#xff1a; CURL的基本使用&#xff1a; CURL与PING命令的区别&#xff1a; CURL命令的应用&#xff1a; 总结&#xff1a; 前言&#xff1a; 当今互联网时代&#xff0c;与服务器进行数据交互成为了无法回避的需求。无论是获取Web…
阅读更多...
电脑入门：电脑不认新硬盘时该怎么办？

电脑入门：电脑不认新硬盘时该怎么办？

电脑不认新硬盘时该怎么办？ 当新硬盘加进后，正常工作时，没有什么问题。若电脑遇到特殊情况时，电脑对新硬盘“不认”，可采取以下措施让电脑重新“认”新硬盘，显示新分区（如G、H、I、J）。 咱的目的是保持S-ATA的开启，把控制板载S-ATA设定值由No变成Yes就可以。 首…
阅读更多...
mysql 8.0.34 安装

mysql 8.0.34 安装

1、进入mysql官网 &#xff1a;https://www.mysql.com/ 拉到最下面&#xff0c;选择社区服务 2、下载mysql服务 msi方式的参考&#xff1a;https://blog.csdn.net/m0_59086544/article/details/129034408。 这里介绍下zip格式的怎么使用&#xff01; 3、 安装服务 下载好 z…
阅读更多...
使用Webpack设置TS引用模块，解决Module not found: Error: Can‘t resolve ‘./m1‘ in ...问题

使用Webpack设置TS引用模块，解决Module not found: Error: Can‘t resolve ‘./m1‘ in ...问题

当我们把ts文件作为模块被引用的时候&#xff0c;我们使用Webpack打包代码会报错&#xff1a; Module not found: Error: Cant resolve ./m1 in ... 解决方法&#xff1a; 在webpack.config.js文件中配置如下代码&#xff1a; module.exports {// 设置引用模块resolve: {ext…
阅读更多...
React 全栈体系（十七）

React 全栈体系（十七）

第九章 React Router 6 一、概述 React Router 以三个不同的包发布到 npm 上&#xff0c;它们分别为&#xff1a; react-router: 路由的核心库&#xff0c;提供了很多的&#xff1a;组件、钩子。react-router-dom: 包含 react-router 所有内容&#xff0c;并添加一些专门用于 …
阅读更多...
解决oss视频上传后截取的第一帧图片被旋转问题

解决oss视频上传后截取的第一帧图片被旋转问题

因此,直接配置参数ar_auto就okpic.url ?x-oss-processvideo/snapshot,t_1000,m_fast,ar_auto
阅读更多...
Unity Game FrameWork—模块使用—资源热更新

Unity Game FrameWork—模块使用—资源热更新

工程选项配置​ json文件解析不要用默认的unity解析方式&#xff0c;unity解析有问题&#xff0c;使用StarForce.LitJsonHelper​ ​ 资源模式改为热更新模式​ ​ 配置文件配置​ BuiltinDataComponent自定义组件引用率了Buildinfo.txt配置文件&#xff0c;该文件配置了热更…
阅读更多...
根据excel批量修改文件夹及其文件名称

根据excel批量修改文件夹及其文件名称

简介 表哥公司电脑上有一大批文件夹&#xff0c;用于存放一些pdf。他希望对这些文件进行整理。文件夹批量重命名为好记一些的名字&#xff0c;文件夹下的pdf改成的名字格式为&#xff1a;文件夹名序号。 例如&#xff1a;文件夹从“1234”&#xff0c;改成“案件001”&#xf…
阅读更多...
Sql注入(手工注入思路、绕过、防御)

Sql注入(手工注入思路、绕过、防御)

一、Sql注入思路 1、判断注入点 在GET参数、POST参数、以及HTTP头部等&#xff0c;包括Cookie、Referer、XFF(X-Forwarded-for)、UA等地方尝试插入代码、符号或语句&#xff0c;尝试是否存在数据库参数读取行为&#xff0c;以及能否对其参数产生影响&#xff0c;如产生影响则…
阅读更多...
Snapdragon Profiler分析Android GPU

Snapdragon Profiler分析Android GPU

Snapdragon Profiler&#xff08;骁龙分析器&#xff09;是一款性能分析软件&#xff0c;在Windows、 Mac、和 Linux平台上都可以运行&#xff0c;主要是用来分析使用了高通骁龙处理器的Android设备。 Snapdragon Profiler通过USB连接这些Android设备&#xff0c;开发者可以用…
阅读更多...
基本页面配置与登录页面编写

基本页面配置与登录页面编写

删除原有的所有初始内容&#xff0c;在views下新建WelcomeView组件 安装vue router 在router下新建index.js文件&#xff0c;编写路由&#xff1a; import {createRouter,createWebHistory} from "vue-router";const routercreateRouter({history:createWebHistor…
阅读更多...
金融生产存储亚健康治理：升级亚健康 3.0 ，应对万盘规模的挑战

金融生产存储亚健康治理：升级亚健康 3.0 ，应对万盘规模的挑战

随着集群规模的不断扩大&#xff0c;硬盘数量指数级上升&#xff0c;信创 CPU 和操作系统、硬盘多年老化、物理搬迁等多种复杂因素叠加&#xff0c;为企业的存储亚健康管理增加了新的挑战。 在亚健康 2.0 的基础上&#xff0c;星辰天合在 XSKY SDS V6.2 实现了亚健康 3.0&#…
阅读更多...
LeetCode【474. 一和零】

LeetCode【474. 一和零】

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度&#xff0c;该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素&#xff0c;集合 x 是集合 y 的 子集 。 示例 1&#xff1a; 输入&#xff1a;strs ["…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023