回忆之前的官方架构图,数据在 storaged 中是分片的,且 raft 协议中只有 leader 才会处理请求,所以,重新进行数据平衡操作,是有可能将多个稠密点分摊到不同的服务上以减轻单一服务的压力。同时,我们对整个集群进行 Compaction 操作(由于 storaged 内部使用了 RocksDB 作为存储引擎,数据是通过追加来进行修改的,Compaction 可以清楚过时的数据,提高访问效率)。
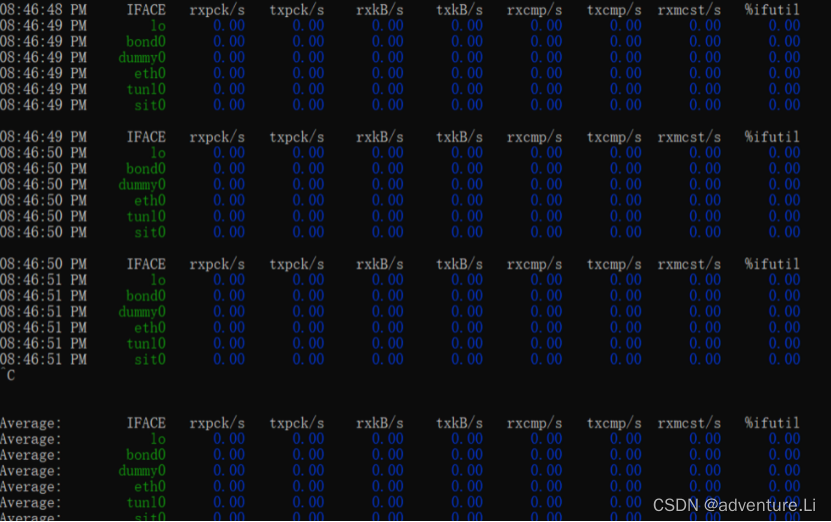
操作之后集群的整体 CPU 是有一定的下降,同时服务的响应速度也有小幅的提升,如下图。


但在运行一段时间之后仍然遇到了 CPU 突然增加的情况,稠密点显然没有被平衡掉,也说明在分片这个层面是没法缓解稠密点带来的访问压力的。
优化稠密点之尝试通过配置缓解锁竞争
进一步调研出现问题的 storaged 的 CPU 的使用率,可以看到当流量增加的时候,内核占用的 CPU 非常高,如下图所示:

抓取 perf 看到,锁竞争比较激烈,即使在 “正常” 情况下,锁的占比也很大,而在竞争激烈的时候,出问题的 storaged 服务上这个比例超过了 50%。如下图所示:

所以我们从减少冲突入手,对 NebulaGraph 集群主要做了如下改动:

重新上线之后,整个集群服务变得比较平滑,CPU 的负载也比较低,正常情况下锁竞争也下降不少(下图),酒店也成功地将流量推送到了 100%。

但运行了一段时间之后,我们仍然遇到了服务响应突然变慢的情况,热点访问带来的压力的确超过了优化带来的提升。
优化稠密点之尝试减小锁的颗粒度
考虑到在分片级别的 balance 不起作用,而 CPU 的上升主要是因为锁竞争造成的,那我们想到如果减小锁的颗粒度,是不是就可以尽可能减小竞争?RocksDB 的 LRUCache 允许调整 shared 数量,我们对此进行了修改:
| 版本 | LRUCache 默认分片数 | 方式 |
|---|---|---|
| v2.5.0 | 2^8 | 修改代码,将分片改成 2^10 |
| v2.6.1 及以上 | 2^8 | 通过配置 cache_bucket_exp = 10,将分片数改为 2^10 |
观察下来效果不明显,无法解决热点竞争导致的雪崩问题。其本质同 balance 操作一样,只是粒度的大小的区别,在热点非常集中的情况下,在数据层面进行处理是走不通的。
优化稠密点之尝试使用 ClockCache
竞争的锁来源是 block cache 造成的。NebulaGraph storaged 使用 RocksDB 作为存储,其使用的是 LRUCache 作为 block cache 等一系列 cache 的存储模块,LRUCache 在任何类型的访问的时候需要需要加锁操作,以进行一些 LRU 信息的更新,排序的调整及数据的淘汰,存在吞吐量的限制。

由于我们主要面临的就是锁竞争,在业务数据没法变更的情况下,我们希望其他 cache 模块来提升访问的吞吐。按照 RocksDB 官方介绍,其还支持一种 cache 类型 ClockCache,特点是在查询时不需要加锁,只有在插入时才需要加锁,会有更大的访问吞吐,考虑到我们主要是读操作,看起来 ClockCache 会比较合适。
LRU cache 和 Clock cache 的区别:https://rocksdb.org.cn/doc/Block-Cache.html
经过修改源码和重新编译,我们将缓存模块改成了 ClockCache,如下图所示: