Kd-Tree:
今天来介绍一下有关Kdtree的相关概念,它是一维线段树的多维推广。Kd-tree常用在激光点云编程中使用,Kd-tree简称k维树,是一种空间划分的数据结构,常被用于高维空间中的搜索,比如范围搜索和最近邻搜索。在激光SLAM中,一般使用的是三维点云,所以kd-tree的维数是3。由于三维点云的数目一般都比较大,所以,使用kd-tree来进行检索可以减少很多时间消耗,可以确保点云的关联点寻找和配准处于实时的状态。
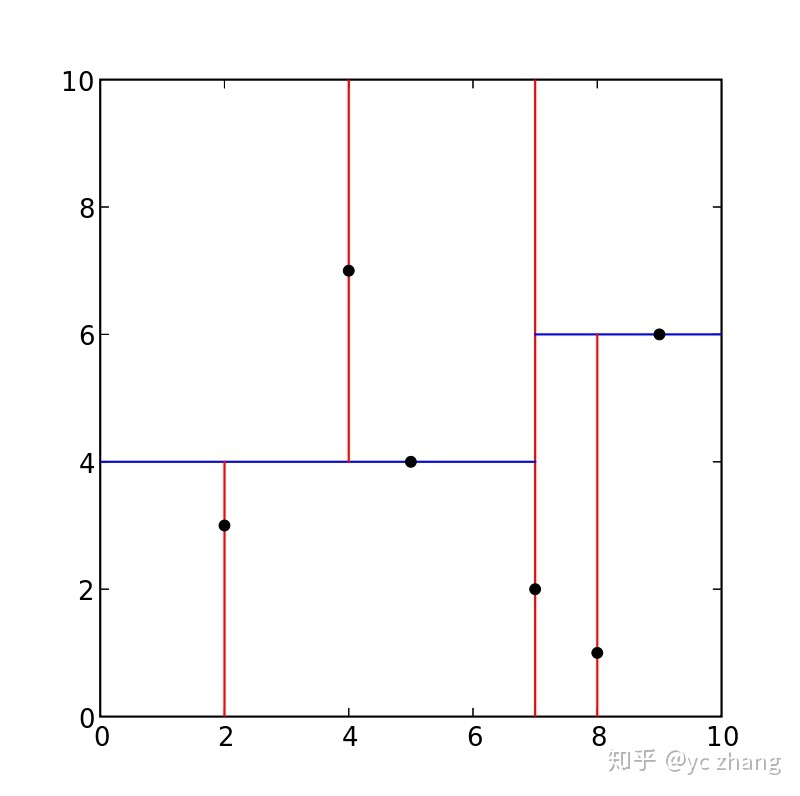
(对于kdtree的数据结构和创建方式就不多说,就是根据树的结构来进行创建,不过在进行树的构建过程中,需要遵守一定的规则,这个规则在下面进行介绍,并且对于二维的情况下面给出一张图来进行kdtree构建的解释说明)
编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面这幅图就是构建kdtree的结果图,大家看到横竖不一的情况首先是虎躯一震。这里我们直接开始讲起,在这里它的划分规则是现根据x轴上的数据选择中点并来上一条垂直于x轴的线进行划分。然后分成两半以后,再根据y轴上的数据选择中点进行划分,然后再选择x轴,再选择y轴,以此重复,直到每个区域里面只有一个点为止。然后根据上述的划分过程来进行kdtree的构建。这样非常简单,然后查找的时候,根据构建树的特点,便会很快查找到位置最近的k个点,并对其进行输出。
说到kdtree,自然而然地提起KNN算法,在激光SLAM里面不使用KNN算法,因为其需要便利所有的激光点,并计算距离,这种做法是得不偿失的。所以不使用KNN,而是用Kdtree来进行激光点云的搜索。
(建树的规则)在构建kdtree的时候,树每往下延伸一层,就会换一个维度作为衡量标准,原因很简单,希望这棵树对于k维空间具有极好的表达能力。
规则一:计算每一维度的方差,然后选择方差较大的维度进行切分,这样做自然是因为方差较大的维度说明数据相对分散,切分之后可以把数据区分得更加明显。但是这样每次划分的过程中需要额外计算方差信息,这无疑增加了计算量。
规则二:轮流选择法,举个例子,如果是二维空间,只有x轴和y轴,那么我们可以从x轴开始进行划分,然后下一次划分的依据则是通过y轴上的数据,然后下下次划分又是通过x轴,这样x轴y轴轮流选择,直到每个区域最多只有一个点为止。
实战:
Kdtree最常用的两个情况:1、最近邻搜索 2、距离范围搜索
代码:
最近邻搜索:
//头文件#include <pcl/kdtree/kdtree_flann.h>//设定kd-tree的智能指针pcl::KdTreeFLANN<pcl::PointXYZI>::Ptr kdtreeCornerLast(new pcl::KdTreeFLANN<pcl::PointXYZI>());//输入三维点云,构建kd-treekdtreeCornerLast->setInputCloud(laserCloudCornerLast);//在点云中寻找点searchPoint的k近邻的值,返回下标pointSearchInd和距离pointSearchSqDiskdtreeCornerLast->nearestKSearch (searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance);
距离范围搜索:
//在点云中寻找和点searchPoint满足radius距离的点和距离,返回下标pointIdxRadiusSearch和距离pointRadiusSquaredDistancekdtreeCornerLast->radiusSearch (searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance)
其实通过代码来看,kdtree的api已经写好了,只需要传进点云数据即可完成相应的操作,里面的函数具体操作,下面进行展示。
#include <pcl/point_cloud.h>#include <pcl/kdtree/kdtree_flann.h>#include <iostream>#include <vector>#include <ctime>intmain (int argc, char** argv){
srand (time (NULL));
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
// Generate pointcloud data cloud->width = 1000;
cloud->height = 1;
cloud->points.resize (cloud->width * cloud->height);
for (std::size_t i = 0; i < cloud->points.size (); ++i)
{
cloud->points[i].x = 1024.0f * rand () / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024.0f * rand () / (RAND_MAX + 1.0f);
cloud->points[i].z = 1024.0f * rand () / (RAND_MAX + 1.0f);
}
pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
kdtree.setInputCloud (cloud);
pcl::PointXYZ searchPoint;
searchPoint.x = 1024.0f * rand () / (RAND_MAX + 1.0f);
searchPoint.y = 1024.0f * rand () / (RAND_MAX + 1.0f);
searchPoint.z = 1024.0f * rand () / (RAND_MAX + 1.0f);
// K nearest neighbor search
int K = 10;
std::vector<int> pointIdxNKNSearch(K);
std::vector<float> pointNKNSquaredDistance(K);
std::cout << "K nearest neighbor search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with K=" << K << std::endl;
if ( kdtree.nearestKSearch (searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0 )
{
for (std::size_t i = 0; i < pointIdxNKNSearch.size (); ++i)
std::cout << " " << cloud->points[ pointIdxNKNSearch[i] ].x
<< " " << cloud->points[ pointIdxNKNSearch[i] ].y
<< " " << cloud->points[ pointIdxNKNSearch[i] ].z
<< " (squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
}
// Neighbors within radius search
std::vector<int> pointIdxRadiusSearch;
std::vector<float> pointRadiusSquaredDistance;
float radius = 256.0f * rand () / (RAND_MAX + 1.0f);
std::cout << "Neighbors within radius search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with radius=" << radius << std::endl;
if ( kdtree.radiusSearch (searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0 )
{
for (std::size_t i = 0; i < pointIdxRadiusSearch.size (); ++i)
std::cout << " " << cloud->points[ pointIdxRadiusSearch[i] ].x
<< " " << cloud->points[ pointIdxRadiusSearch[i] ].y
<< " " << cloud->points[ pointIdxRadiusSearch[i] ].z
<< " (squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
}
return 0;}
啊,上面的函数里面又嵌套了pcl官方文档已经写好的函数,没啥好读的,大体思想知道了这个kdtree就是一个搜索的工具,也算是一种算法吧。
本篇kdtree介绍就到这里,这个内容在激光SLAM里面可能会用得到,具体思想也在上面,还是多看看例子,知道这个东西是怎么回事即可。