前言
高斯在处理正态分布的首次提出似然,后来英国物理学家,费歇尔

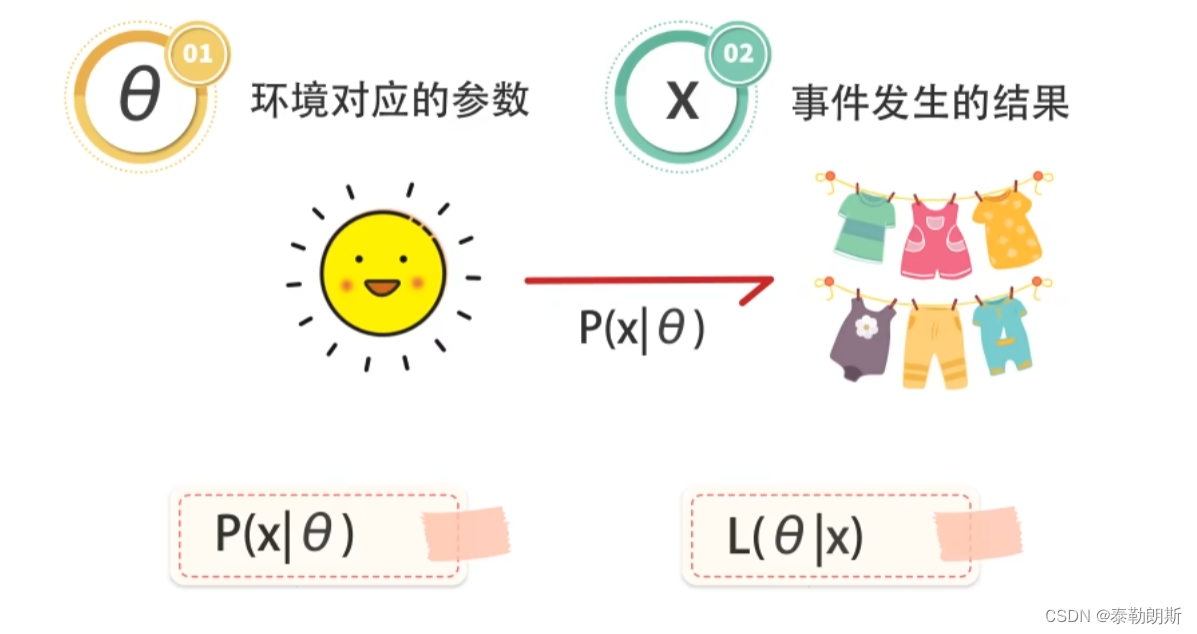
概率是抛硬币之前,根据环境推断概率

似然则相反,根据结果推论环境

P是关于x的函数,比如x为正面朝上的结果,或者反面朝上的结果,比如x=正面朝上的时候,概率
θ
\theta
θ是多少
L是关于
θ
\theta
θ的函数,就是说某一个概率值下,最有可能出现的结果
极大似然估计是根据已知的观察数据来推断模型参数的过程,根据x的结果推断
θ
\theta
θ,,结果x最有可能发生。
举例来说
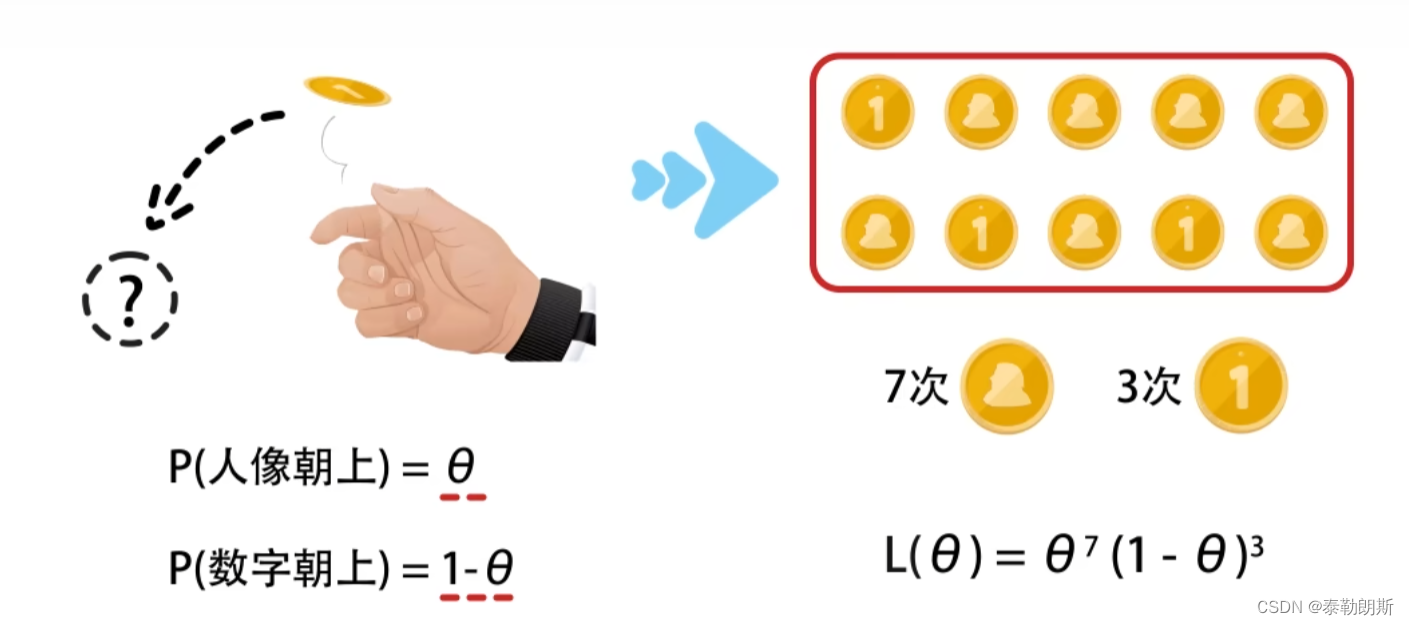
函数在
θ
\theta
θ未0.7的时候取得最大值
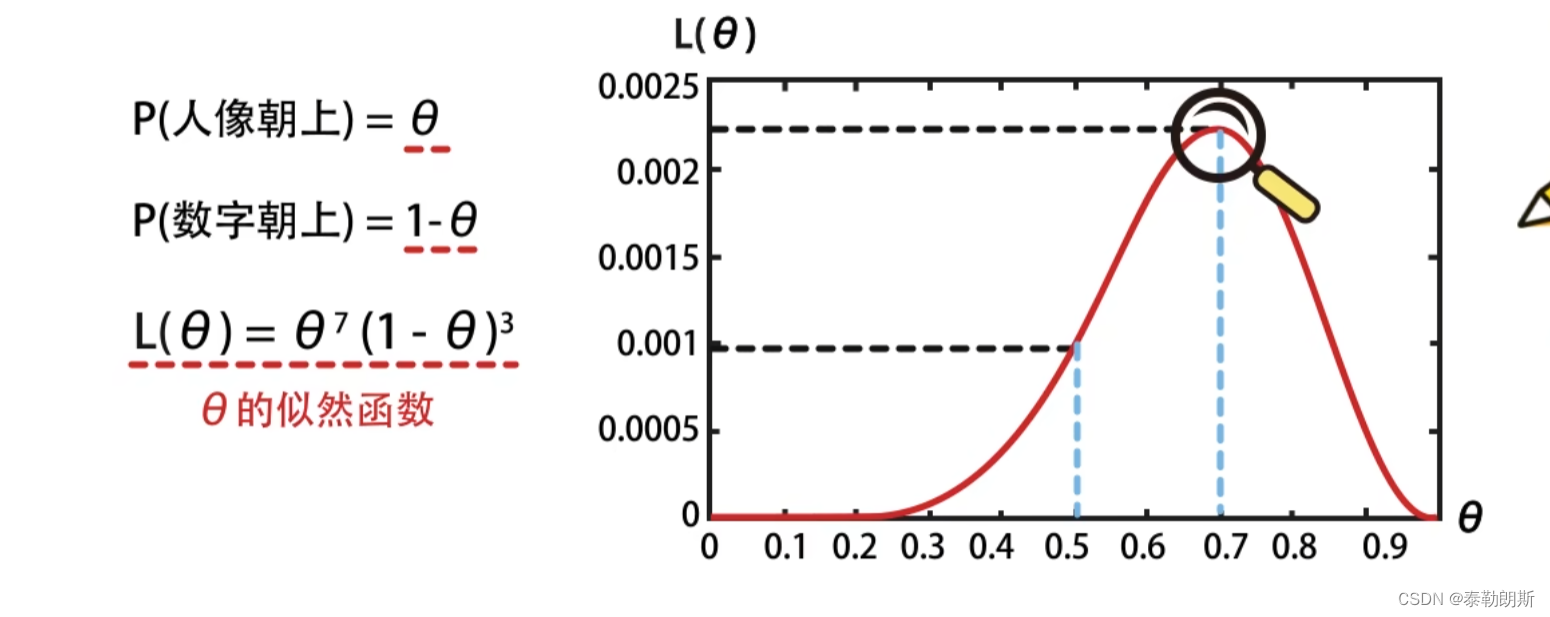
当
θ
\theta
θ为多少时,出现7次正面,3次反面
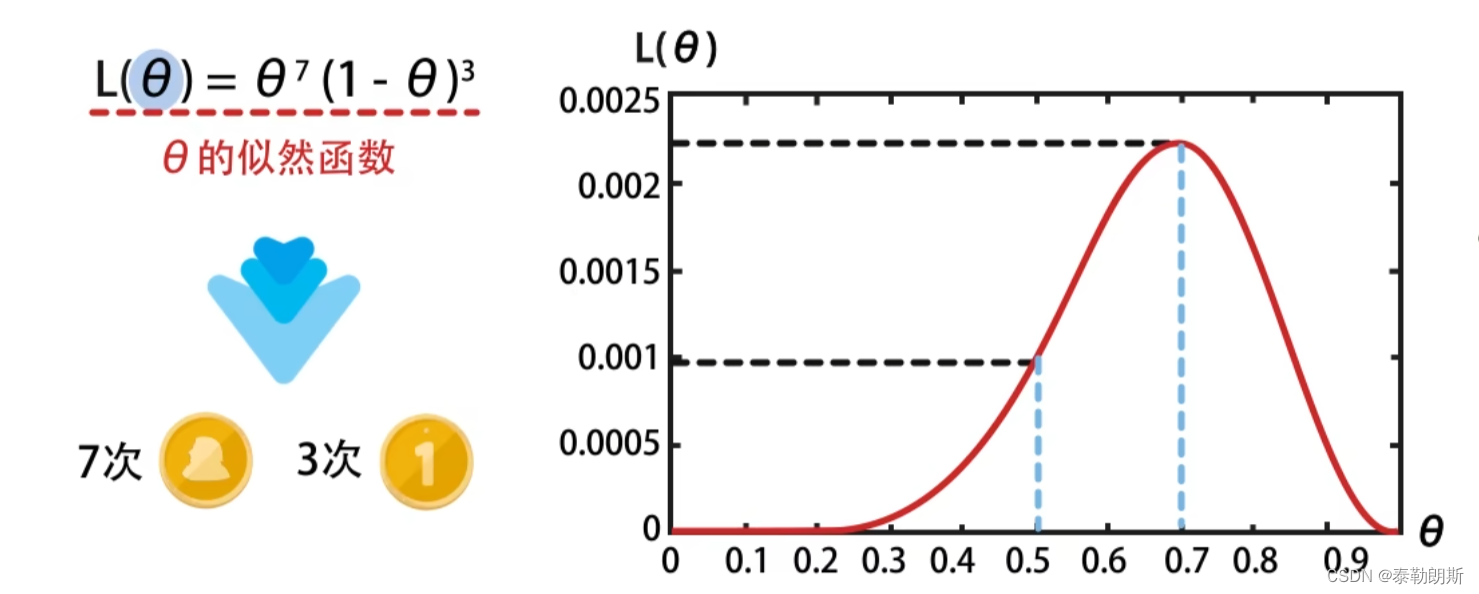
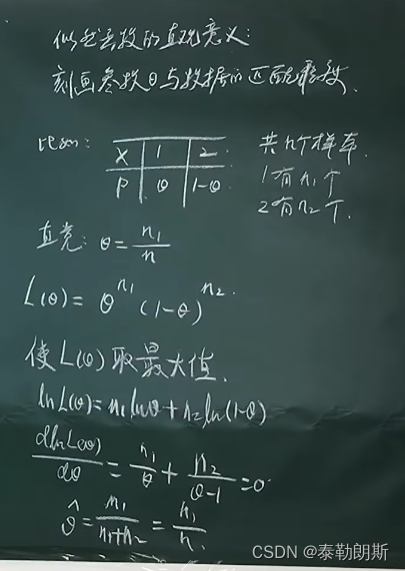
总结
我觉得可以这样理解:
似然函数描述的是当前已经取得的样本的概率分布F,F是
θ
\theta
θ的函数,因为
θ
\theta
θ是未知的,所以F的具体值由
θ
\theta
θ的取值来确定。 那么,
θ
\theta
θ取哪个值才能“最恰当”的描述我们取得的这组样本呢? 因为我只有手头这些样本,既然就这么巧就拿到了这些,我就认为出现手头这些样本的概率是最大的。似然函数描述的是手头这些样本的概率,最大化似然函数
f
(
θ
)
f(\theta)
f(θ),就可以得到
θ
\theta
θ值了。 关键在于,我们就这么巧,拿到的手头这些样本,那么手头这些样本出现的概率就是最大的, 可以这样理解极大似然!
比如上文中,只有
θ
=
0.7
\theta=0.7
θ=0.7的时候,
f
(
θ
)
f(\theta)
f(θ)的值最大。
那么这个函数是怎么推导出来的,或者说是谁发现这个函数有这个性质呢?留给你
上面只有两个概率分布,那么多个概率分布呢,比如筛子6个面。
最大熵模型中的对数似然函数的解释
怕你看不懂,解释一下,下面的
x
1
,
x
2
,
x
3
.
.
.
x_1,x_2,x_3...
x1,x2,x3...指的是我们上面筛子中的1-6中的某个点(其余案例阔以按照这个扩散),
θ
\theta
θ 就是出现这个点数的概率。
比如十次,1-6出现的次数依次是,5,1,1,1,1,1
那么最大似然就是:
L
p
=
0.
5
5
∗
0.
1
1
∗
0.
1
1
∗
0.
1
1
∗
0.
1
1
∗
0.
1
1
L_p=0.5^5*0.1^1*0.1^1*0.1^1*0.1^1*0.1^1
Lp=0.55∗0.11∗0.11∗0.11∗0.11∗0.11,这样的时候L最大。