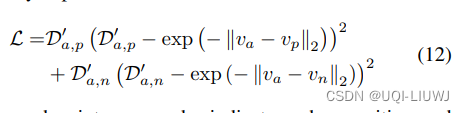2022 KDD

1 intro

• 现有的轨迹相似性学习方案强调空间相似性而忽视了时空轨迹的时间维度，这使得它们在有时间感知的场景中效率低下
  • 
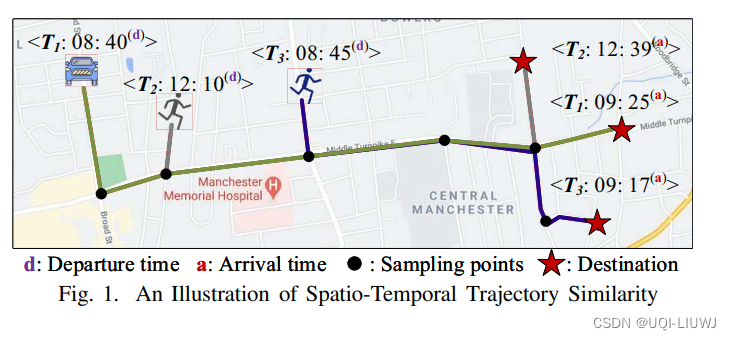
    • 如上图，在拼车过程中，T1表示司机计划的行程，T2和T3是两个想要搭车的人。
    • T1和T2在空间上更接近，因此仅考虑空间相似性的算法会推荐T2。然而，T1和T2的出发时间相去甚远。
    • T3虽然距T1空间上较远，但却和T1是相近的出发时间。
    • 因此，从时空两方面考虑，应选择T3。
• 实现道路网络中的时空轨迹相似性学习有两种方法，
  • 一种是将时间划分为时间片，然后分别处理空间和时间
    • 但问题是对时间维度的粗粒度离散化并不能充分利用时间信息。
  • 另一种更有前途的方向是学习统一的时空嵌入，以捕捉轨迹之间复杂的时空相似性
    • 现有研究仍有三个重大挑战有待解决：
      • 一是时间嵌入，如何捕捉轨迹之间的时间相关性生成嵌入。
        • 由于时间的连续性以及轨迹的周期性，直接将时间序列输入递归神经网络（RNN）模型是无效的。
      • 二是时空融合，如何融合嵌入实现统一的时空相似性学习。
      • 三是模型优化，如何提高有效性（即相似度查询质量）和效率（即模型收敛速度）
• ——>论文提出了ST2Vec，一种基于轨迹表征学习的架构。
  • 它考虑了轨迹之间的细粒度时空相关性，很好地解决了三大挑战。
  • 文章还提到，这是第一个关于时空轨迹相似性分析的深度学习方案

2 问题定义

2.1 路网

• 一个有向图G=(L,E)，顶点li=(xi, yi)∈L模拟道路的交叉口或道路末端。
  • 其中x，y分别为经纬度。
  • 边eli,lj∈E模拟了一个从li到lj的定向路段。

2.2 时空轨迹序列

• T=<(g1,t1),(g2,t2),...,(gn,tn)>，g为观测到的由经度和纬度组成的地理位置，t为对应的时间。

2.3 时空相似性

• 时空轨迹相似性函数D(Ti,Tj)。
  • 
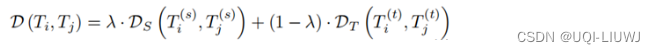
    • DS和DT分别表示空间和时间上的相似性。
    • λ∈[0,1]控制了空间和时间相似性的相对权重，提高了灵活性。

2.5 学习目标

• 时空轨迹相似性学习的目的是学习一个神经网络驱动的函数G(·,·)，使G(vTi，vTj)最大接近于D(Ti,Tj)
  • 

    • M为神经网络的模型参数。

    • vTi和vTj是时空轨迹Ti和Tj的时空嵌入中。

    • D是一些路网下的轨迹相似度度量，比如 TP, DITA, LCRS,NetERP 等

3 模型

3.1 整体模型

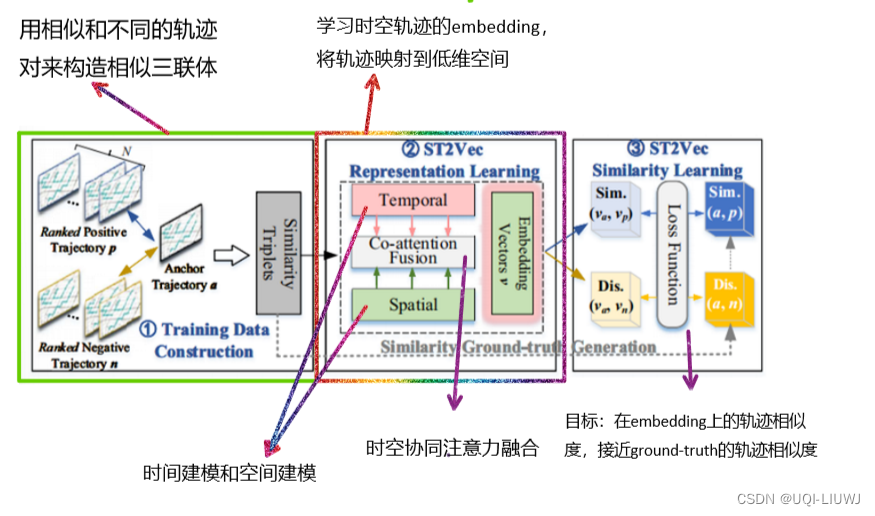
3.2 ST2Vec 时空轨迹嵌入

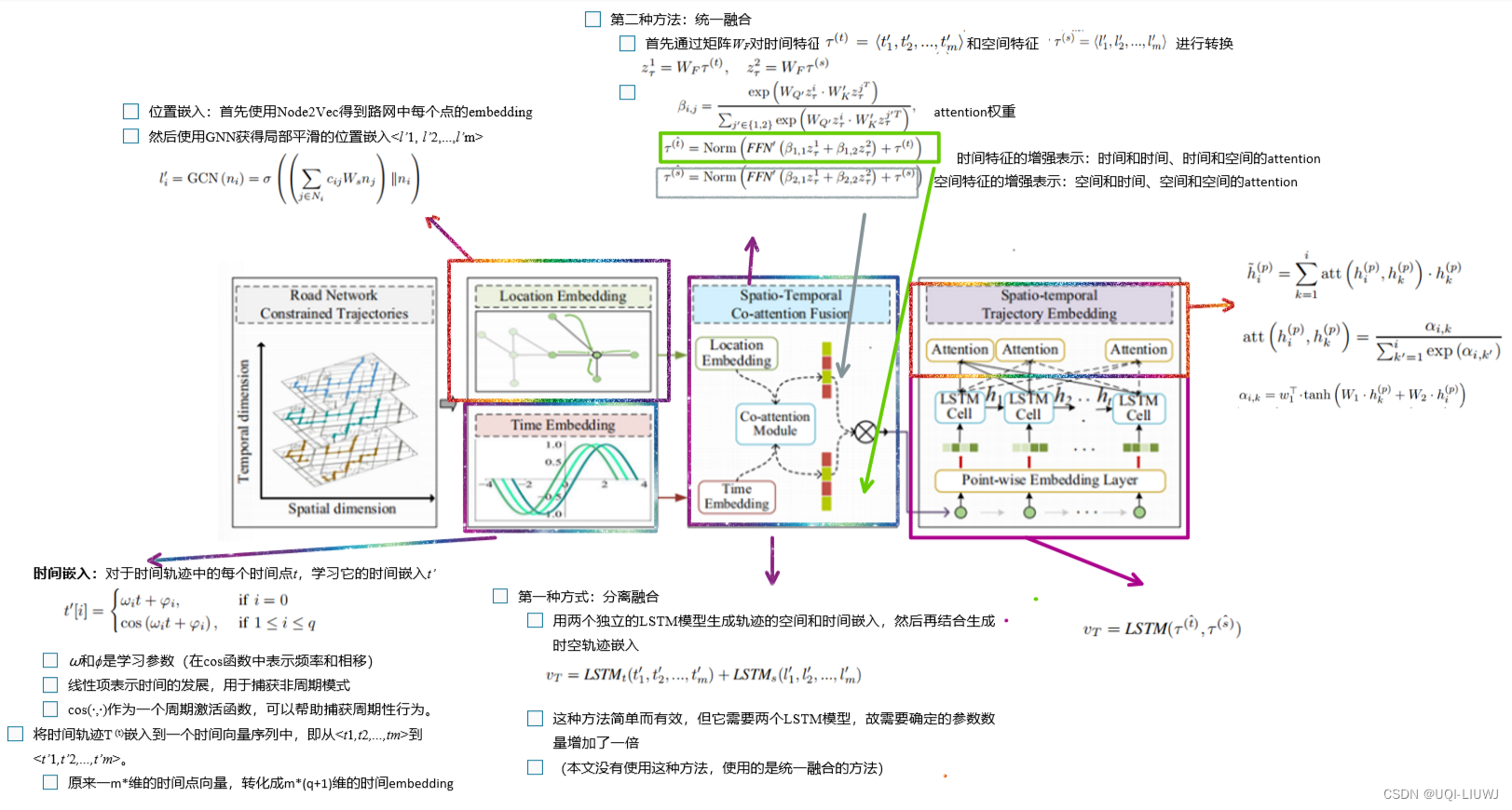
3.3 训练过程

• 选择一条锚点轨迹时，我们会找到其 N 个最相似的轨迹作为相似的轨迹。忽略相似的轨迹，我们随机选择 N 个其他轨迹作为不相似的轨迹
• 损失函数：
  • 

4 实验

4.1 效果

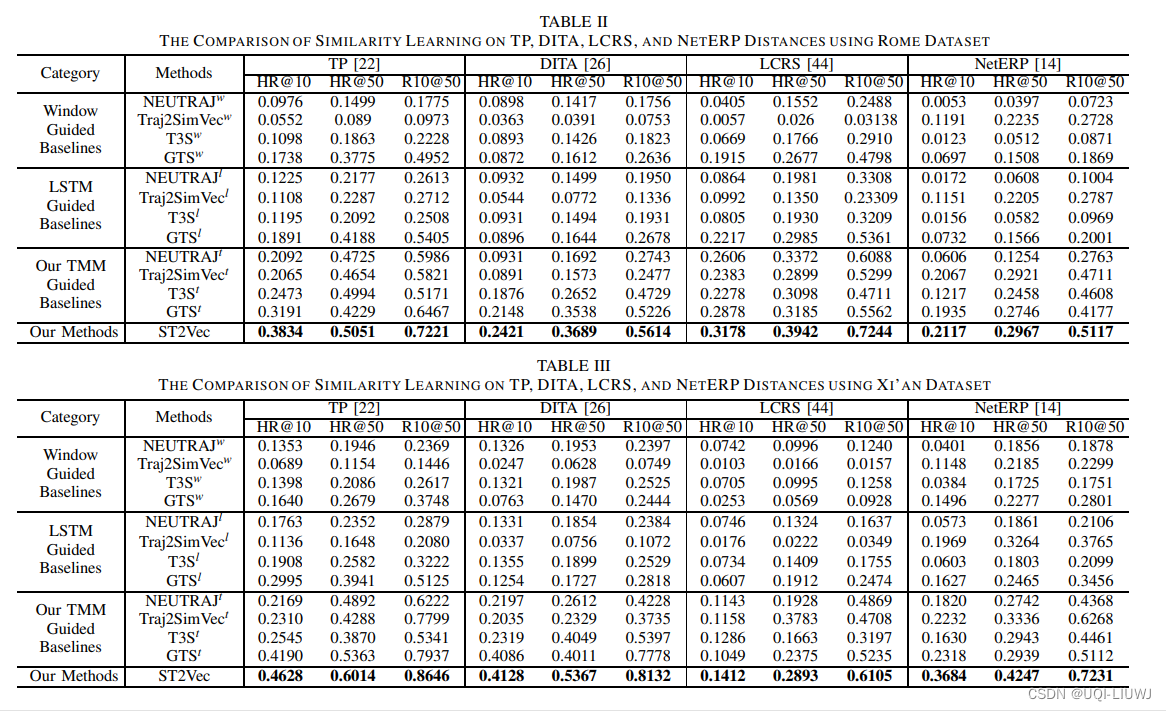
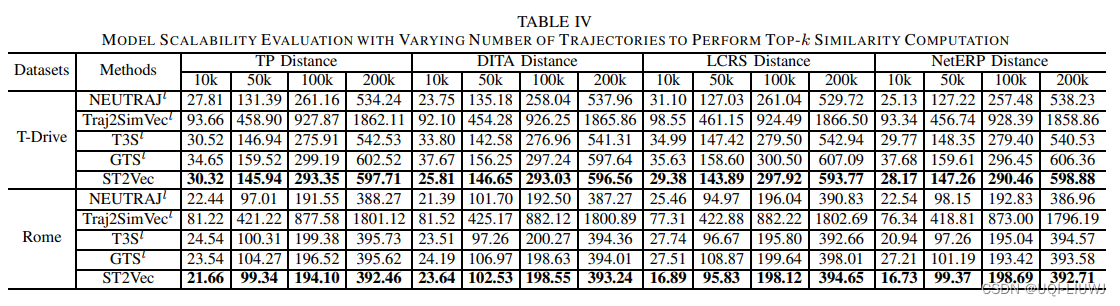
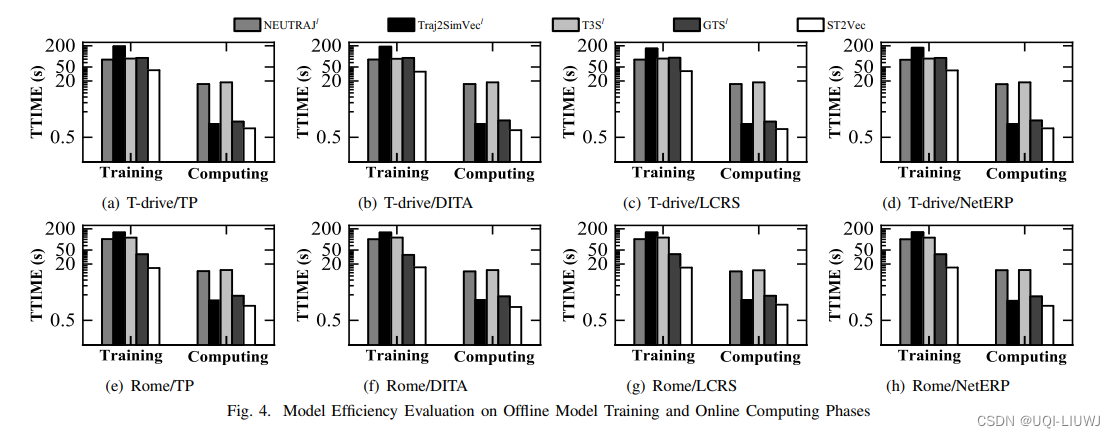
4.2 scalability