LRU、LFU 内存淘汰算法的设计与实现

1、背景介绍

LRU、LFU都是内存管理淘汰算法，内存管理是计算机技术中重要的一环，也是多数操作系统中必备的模块。应用场景：假设给定你一定内存空间，需要你维护一些缓存数据，LRU、LFU就是在内存已经满了的情况下，如果再次添加新的数据，该淘汰哪些数据来留出新数据的内存空间？？？

2、LRU(least recently used)

LRU(east recently used)，即最近最少使用 ，也就是说在内存满的情况下，将会淘汰很久都没有使用过的数据。例如 leetcode 146题。

需求：现在需要设计一个算法，使得插入新数据、获取已经存入的数据，使得平均时间复杂度O(1)。

设计思路：因为插入、获取数据时，都会更新时间戳，还需要使得平均时间复杂度O(1)，可以使用双链表+哈希表的方式来存储。

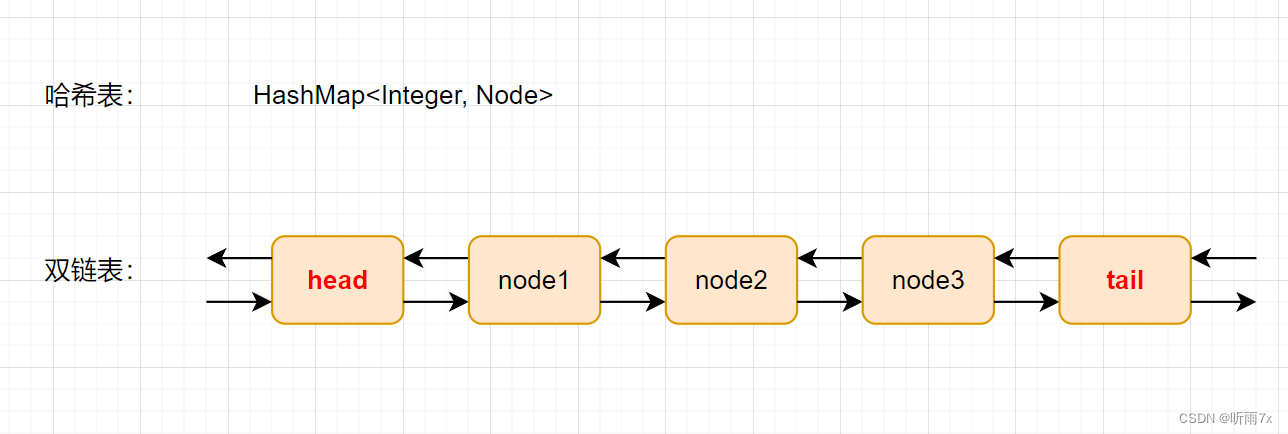
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

如上图，哈希表里存储键与双链表节点，双链表的head表示最近使用过的数据，tail表示很久都没使用过的数据。

插入数据时，在哈希表建立key与Node节点，然后把Node节点插入双链表的头部位置。
获取数据时，从哈希表拿到Node节点，然后把Node节点从双链表中分离出来，插入双链表的头部位置即可。

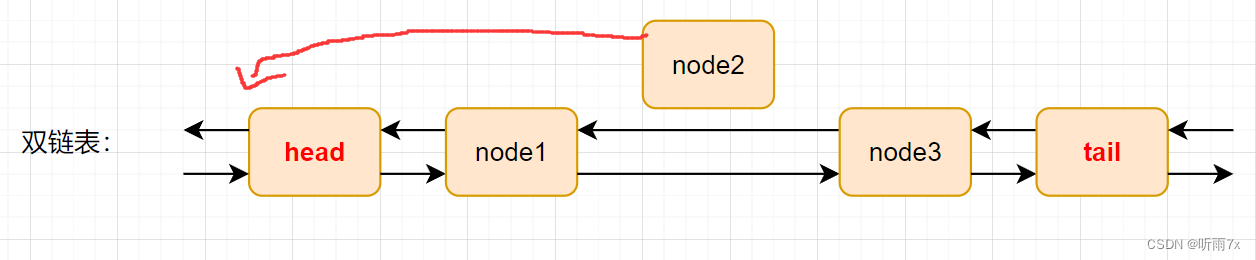
以上两个步骤，时间复杂度都是O(1)。所以符合题意。

代码如下：

// lc146题 直接能过的代码
class LRUCache {
    // LRU，最近最少使用
    // 用双链表节点包装进行连接
    private HashMap<Integer, Node> map; // 哈希表，存储key与双链表节点
    private int maxSize; // 缓存的最大容量
    private Node head, tail; // 头部是最近使用的，尾部 是很久没使用的
    
    private static class Node { // 双链表节点
        int key, val;
        Node left, right;
        public Node(int k, int v) {
            key = k;
            val = v;
        }
    }
    
    public LRUCache(int capacity) {
        map = new HashMap<>();
        maxSize = capacity;
    }
    
    public int get(int key) {
        if(!map.containsKey(key)) return -1;
        Node node = map.get(key);
        if (node == head) return node.val;
        apart(node); //分离出node节点
        node.right = head; // 插入到双链表的头部位置
        head.left = node;
        head = node;
        return node.val;
    }
    
    public void put(int key, int value) {
        if (!map.containsKey(key)) {
            Node node = new Node(key, value);
            node.right = head;
            if (head != null) head.left = node;
            if (tail == null) tail = node;
            head = node;
            map.put(key, node);
            if (map.size() > maxSize) { // 容量超了，删除双链表的尾部元素
                if (tail.left != null) {
                    tail.left.right = null;
                }
                map.remove(tail.key);
                Node pre = tail.left;
                tail.left = null;
                tail = pre;
            }
        } else {
            Node node = map.get(key);
            node.val = value;
            get(key); // 调用get，使其向前移动
        }
    }

    // node的左右两边连接，将node抽离出
    private void apart(Node node) {
        node.left.right = node.right;
        if (node.right != null) {
            node.right.left = node.left;
        }
        if (node == tail) {
            tail = node.left;
        }
        node.left = node.right = null;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

3、LFU(least frequancy used)

LFU(least frequancy used), 即不常用算法，按照每个数据的访问次数来判断数据的使用情况。如果一个数据在近一段时间内没有被访问或者被访问的可能性小，则会被淘汰。（简单点说，就是按照“使用频率”来分级的）例题：leetcode 460题

需求：现在需要设计一个算法，使得插入、获取数据的平均时间复杂度O(1)。

设计思路：按照使用频率进行划分，相同频率的数据放在同一个“桶”内，从左往右频率逐渐升高；而桶内部是从上往下，按照插入桶内的时间来排序，新插入的节点在桶的顶部，很久之前插入的节点在桶的底部，如下图所示：

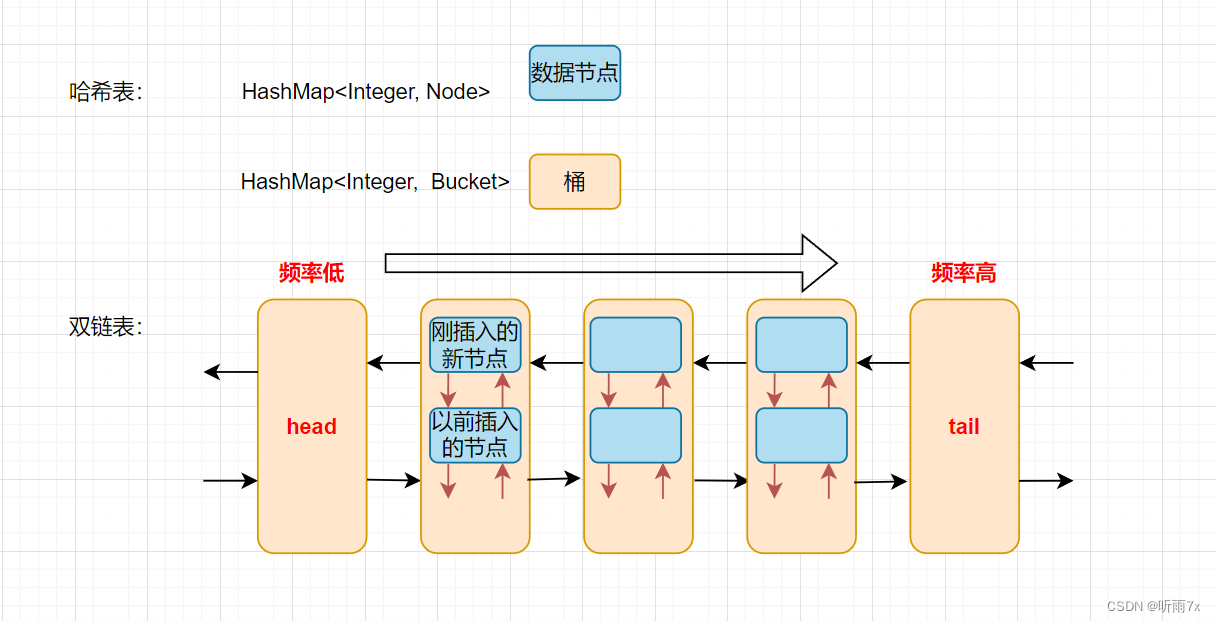
在这里插入图片描述

注意：当内存满了的时候，会删除 频率最低的桶内，最后的一个数据节点。

代码实现如下：

public class LFUCache {
	public LFUCache(int K) {
		capacity = K;
		size = 0;
		records = new HashMap<>();
		heads = new HashMap<>();
		headList = null;
	}

	private int capacity; // 缓存的大小限制，即K
	private int size; // 缓存目前有多少个节点
	private HashMap<Integer, Node> records;// 表示key(Integer)由哪个节点(Node)代表
	private HashMap<Node, NodeList> heads; // 表示节点(Node)在哪个桶(NodeList)里
	private NodeList headList; // 整个结构中位于最左的桶

	// 节点的数据结构
	public static class Node {
		public Integer key;
		public Integer value;
		public Integer times; // 这个节点发生get或者set的次数总和
		public Node up; // 节点之间是双向链表所以有上一个节点
		public Node down;// 节点之间是双向链表所以有下一个节点

		public Node(int k, int v, int t) {
			key = k;
			value = v;
			times = t;
		}
	}

	// 桶结构
	public static class NodeList {
		public Node head; // 桶的头节点
		public Node tail; // 桶的尾节点
		public NodeList last; // 桶之间是双向链表所以有前一个桶
		public NodeList next; // 桶之间是双向链表所以有后一个桶

		public NodeList(Node node) {
			head = node;
			tail = node;
		}

		// 把一个新的节点加入这个桶，新的节点都放在顶端变成新的头部
		public void addNodeFromHead(Node newHead) {
			newHead.down = head;
			head.up = newHead;
			head = newHead;
		}

		// 判断这个桶是不是空的
		public boolean isEmpty() {
			return head == null;
		}

		// 删除node节点并保证node的上下环境重新连接
		public void deleteNode(Node node) {
			if (head == tail) {
				head = null;
				tail = null;
			} else {
				if (node == head) {
					head = node.down;
					head.up = null;
				} else if (node == tail) {
					tail = node.up;
					tail.down = null;
				} else {
					node.up.down = node.down;
					node.down.up = node.up;
				}
			}
			node.up = null;
			node.down = null;
		}
	}

	// removeNodeList：刚刚减少了一个节点的桶
	// 这个函数的功能是，判断刚刚减少了一个节点的桶是不是已经空了。
	// 1）如果不空，什么也不做
	//
	// 2)如果空了，removeNodeList还是整个缓存结构最左的桶(headList)。
	// 删掉这个桶的同时也要让最左的桶变成removeNodeList的下一个。
	//
	// 3)如果空了，removeNodeList不是整个缓存结构最左的桶(headList)。
	// 把这个桶删除，并保证上一个的桶和下一个桶之间还是双向链表的连接方式
	//
	// 函数的返回值表示刚刚减少了一个节点的桶是不是已经空了，空了返回true；不空返回false
	private boolean modifyHeadList(NodeList removeNodeList) {
		if (removeNodeList.isEmpty()) {
			if (headList == removeNodeList) {
				headList = removeNodeList.next;
				if (headList != null) {
					headList.last = null;
				}
			} else {
				removeNodeList.last.next = removeNodeList.next;
				if (removeNodeList.next != null) {
					removeNodeList.next.last = removeNodeList.last;
				}
			}
			return true;
		}
		return false;
	}

	// 函数的功能
	// node这个节点的次数+1了，这个节点原来在oldNodeList里。
	// 把node从oldNodeList删掉，然后放到次数+1的桶中
	// 整个过程既要保证桶之间仍然是双向链表，也要保证节点之间仍然是双向链表
	private void move(Node node, NodeList oldNodeList) {
		oldNodeList.deleteNode(node);
		// preList表示次数+1的桶的前一个桶是谁
		// 如果oldNodeList删掉node之后还有节点，oldNodeList就是次数+1的桶的前一个桶
		// 如果oldNodeList删掉node之后空了，oldNodeList是需要删除的，所以次数+1的桶的前一个桶，是oldNodeList的前一个
		NodeList preList = modifyHeadList(oldNodeList) ? oldNodeList.last : oldNodeList;
		// nextList表示次数+1的桶的后一个桶是谁
		NodeList nextList = oldNodeList.next;
		if (nextList == null) {
			NodeList newList = new NodeList(node);
			if (preList != null) {
				preList.next = newList;
			}
			newList.last = preList;
			if (headList == null) {
				headList = newList;
			}
			heads.put(node, newList);
		} else {
			if (nextList.head.times.equals(node.times)) {
				nextList.addNodeFromHead(node);
				heads.put(node, nextList);
			} else {
				NodeList newList = new NodeList(node);
				if (preList != null) {
					preList.next = newList;
				}
				newList.last = preList;
				newList.next = nextList;
				nextList.last = newList;
				if (headList == nextList) {
					headList = newList;
				}
				heads.put(node, newList);
			}
		}
	}

	public void put(int key, int value) {
		if (capacity == 0) {
			return;
		}
		if (records.containsKey(key)) {
			Node node = records.get(key);
			node.value = value;
			node.times++;
			NodeList curNodeList = heads.get(node);
			move(node, curNodeList);
		} else {
			if (size == capacity) {
				Node node = headList.tail;
				headList.deleteNode(node);
				modifyHeadList(headList);
				records.remove(node.key);
				heads.remove(node);
				size--;
			}
			Node node = new Node(key, value, 1);
			if (headList == null) {
				headList = new NodeList(node);
			} else {
				if (headList.head.times.equals(node.times)) {
					headList.addNodeFromHead(node);
				} else {
					NodeList newList = new NodeList(node);
					newList.next = headList;
					headList.last = newList;
					headList = newList;
				}
			}
			records.put(key, node);
			heads.put(node, headList);
			size++;
		}
	}

	public int get(int key) {
		if (!records.containsKey(key)) {
			return -1;
		}
		Node node = records.get(key);
		node.times++;
		NodeList curNodeList = heads.get(node);
		move(node, curNodeList);
		return node.value;
	}
}