姿态估计的作用?
姿态估计是飞控算法的一个基础部分,而且十分重要。为了完成飞行器平稳的姿态控制,首先需要精准的姿态数据作为控制器的反馈。
飞控姿态估计的难点?
姿态估计的一个难点主要是一般选用的惯性传感器,都是MEMS器件,精度相对较差;此外,实际工作中很难准确的判定姿态估计的是否准确。
姿态估计的指标?
一般考虑三个性能,收敛性、精确性、准确性。
Ø 收敛性:即估计出的姿态角数据不会轻易发散,在动态变化时,能很快的收敛到对应的角度;
Ø 精确性:比如飞行器放置不动,此时得到的姿态角在0度左右波动,这个波动范围即考虑的精确性;
Ø 准确性:这个比较难以考究,即没办法确定所得到的角度的精确程度。一般用外部参考的方法测量,比如飞机上同时挂载自己的飞控以及高精度的IMU设备(比如xsens、sbg等),飞行完成后,对比自己飞控所解算的角度和外部设备的误差;又或者,在室内装vicon设备来给出外部参考。注意,验证算法的时候,最好还是用实际飞行的数据,否则加速度噪声对算法的影响无法验证。
需要什么基础?即在进行姿态估计前需要做什么?
主要对传感器数据进行校准、滤波,陀螺仪、加速度、地磁的数据预处理以及滤波算法请看专栏或公众号的其他文章。
本文主要从工程角度去实现姿态估计算法,相应的理论知识也可见其他文章。
姿态估计如何做?
一言以蔽之,根据陀螺仪的角度数据高频特性好,而加速度计和地磁计得到的角度数据低频特性好,从而进行互补,得到最优角度。无论什么算法,本质都是陀螺仪积分得到角度,然后根据加速度计和地磁计修正积分的漂移误差。
工程上每个算法的引入都是为了解决问题的,所以下面将从简单的互补开始,逐步解释每个算法的优缺点。
1、 记录实际飞行数据,需要保存陀螺仪、加速度、地磁计数据;
如图所示:

笔者这里采用了现成的模块,所以有参考的角度数据。

2、对好数据坐标系
即调整数据的正负号,初学者往往会忽略这一点,这个在姿态估计算法中非常重要,很多人经常有疑问,为什么自己移植别人的代码,一模一样,但是自己就得不到正确的结果,往往原因都在这里。
这里笔者以前右下(xyz)为机体系,另外如果飞行数据噪音很大,可以在仿真中做滤波处理。
3、分析单独的陀螺仪积分角度与加速度计计算得到的角度数据
方法:
角速度数据直接积分;
加速度数据:
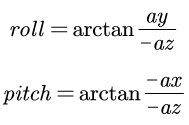
代码:
%对比角速度积分与加速度得到的姿态角之间的区别
%角速度积分得到的角度会随时间漂移
%加速度得到的角度会噪声很大
roll_gyro = zeros(m,1);
roll_acc = zeros(m,1);
for i = 2:m
if i==1
roll_gyro(1) = gx(1) * dt;
else
roll_gyro(i) = roll_gyro(i-1) + gx(i) * dt;
end
roll_acc(i) = atan2(ay(i),-az(i));
end
figure(4)
plot(t1,roll_gyro,t1,roll_acc,'r');title('roll 角速度、加速度推角度对比');xlabel('Time(s)');grid;
pitch_gyro = zeros(m,1);
pitch_acc = zeros(m,1);
for i = 2:m
if i==1
pitch_gyro(1) = gy(1) * dt;
else
pitch_gyro(i) = pitch_gyro(i-1) + gy(i) * dt;
end
pitch_acc(i) = atan2(-ax(i),-az(i));
end
figure(5)
plot(t1,pitch_gyro,t1,pitch_acc,'r');title('pitch 角速度、加速度推角度对比');xlabel('Time(s)');grid;
仿真结果:


如上图所示,蓝色的陀螺积分角度随着时间会有漂移,而加速度计得到的角度则噪声很大,都无法使用(这里的数据不是飞行数据,所以噪声很小)。
所以,既然单独的角度都各自有缺陷,而恰好一个有漂移一个没有漂移,一个噪音大一个噪音小,很自然能联想到用互补的办法,每个周期的最优角度为两者加权得到。
4、线性互补滤波
通过设置一个权重值,让每个周期得到的角度由两个数据源共同作用,还可以通过调节权重值,选择是更相信陀螺仪还是加速度。
代码:
%互补滤波 单轴
complementation_filtered = zeros(m,1);
adaption_complementation_filtered = zeros(m,1);
coeff = 0.75;
for i=2:m
complementation_filtered(i) = (complementation_filtered(i-1) + gx(i)*dt) * coeff + (1 - coeff) * roll_acc(i);
if abs(gx(i)) > 0.2
adaption_complementation_filtered(i) = (adaption_complementation_filtered(i-1) + gx(i)*dt) * coeff + (1 - coeff) * roll_acc(i);
else
adaption_complementation_filtered(i) = (adaption_complementation_filtered(i-1) + gx(i)*dt) * 0.005 + (1 - 0.005) * roll_acc(i);
end
end
figure(6)
subplot(411)
title('滚转');
plot(t1,complementation_filtered,'r',t1,roll_gyro);grid;
legend('互补滤波','角速度积分')
subplot(412)
plot(t1,complementation_filtered,'r',t1,roll_acc);grid;
legend('互补滤波','加速度参考')
subplot(413)
plot(t1,complementation_filtered,'r',t1,roll);grid;
legend('互补滤波','参考角度')
subplot(414)
plot(t1,adaption_complementation_filtered,'r',t1,roll);grid;
legend('自适应互补','参考角度')仿真结果:

首先我们可以看出互补滤波的结果不再像陀螺仪角度那样,随着时间漂移。实际飞行时,固定的权重值很难找到理想值,要不陀螺仪的权重大了,动态性能还可以,大致能跟上角度,但是不能静态保持;加速度权重大了,噪音大,另外动态性能差,原地来回摆动时,得到的角度幅值会很小,这里的数据很难看出这个问题。
所以最好是当飞行器在动态过程时,我们更相信陀螺仪,反之,飞行器静止时,又更相信加速度计。即参数进行自适应调整。
代码:
判定角速度数据,大于一定阈值,认为在运动,所以加大陀螺仪权重。
5、卡尔曼滤波
作为状态估计常用的算法,卡尔曼滤波的卡尔曼增益是动态调整的,所以这一点比固定权重的线性互补滤波要好,此外要注意的是卡尔曼的效果好坏与所选用的状态变量,建立的模型有很大关系,不可一概而论卡尔曼就一定很好,具体情况具体分析。
因卡尔曼滤波的使用条件是针对线性模型,且状态分布为高斯分布,所以这里建立两种线性模型,对比仿真结果。
模型一:
状态量为角度和角速度偏移,这里认为角速度偏移为常值,即角度是上一时刻的角度加(减)角速度偏移的角度,再加上角速度积分的增量。
![]()
转换成状态空间形式:

代码:
%单轴kalman 模型1
Q_angle = 0.1;
Q_bias = 0.01;
R_angle = 10;
Q = [Q_angle 0; 0 Q_bias];
pitchKF1 = zeros(m,1);
pitchMeasure1 = zeros(m,1);
bias = zeros(m,1);
P = [0 0
0 0];
C = [1 0];
for i = 2:m
pitchMeasure1(i) = atan2(-ax(i),-az(i));
A = [1 -dt; 0 1];
%Predicted state estimate x = F.x + B.u
pitchKF1(i) = pitchKF1(i-1) + dt * (gy(i) - bias(i-1));
bias(i) = bias(i-1);
%Predicted estimate covariance P = F.P.F' + Q
P = A*P*A' + Q;
%Innovation y = z - H.x
y = pitchMeasure1(i) - pitchKF1(i);
%Innovation covariance S = H.P.H' + R
S = C*P*C' + R_angle;
%Optimal kalman gain K = P.H'/S
K = P * C' / S;
%Updated state estimate x=x + K.y
pitchKF1(i) = pitchKF1(i) + K(1)*y;
bias(i) = bias(i) + K(2)*y;
%Updated estimate covariance P = (I - K.H).P
P = ([1 0; 0 1] - [K(1); K(2)] * C) * P;
end
figure(7)
plot(t1,pitchKF1,t1,pitch,'r');title('单轴卡尔曼模型结果验证');xlabel('Time(s)');grid;
legend('单轴卡尔曼','参考角度')仿真结果:

放大图像:

可以看出,此算法基本能得到正确结果,除了在某些地方跟踪不好,具体原因后面再讲。
模型二:
状态量分别是俯仰角、滚转角以及对应的角速度偏移。与上面的模型相比,这里我们将水平方向的两轴姿态合并在一起,这样易于代码实现,否则在软件中需针对三个轴进行三次调用。
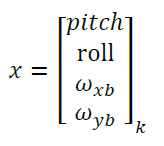
模型如下:

代码:
%两轴kalman 模型2
pitchKF2 = zeros(m,1);
rollKF2 = zeros(m,1);
bp = zeros(m,1);
bq = zeros(m,1);
pitchMeasure2 = zeros(m,1);
rollMeasure2 = zeros(m,1);
P_out = zeros(m,4,4);
Q_pitch = 0.001; %Calculated from data
Q_roll = 0.001; %Calculated from data
Q_bp = 0.1;
Q_bq = 0.1;
R_pitch = 5; %Accel variance, calculated from data
R_roll = 5; %Accel variance, calculated from data
Q = [Q_pitch 0 0 0
0 Q_roll 0 0
0 0 Q_bp 0
0 0 0 Q_bq];
R = [R_pitch 0 0 0
0 R_pitch 0 0
0 0 0 0
0 0 0 0];
P = [0 0 0 0
0 0 0 0
0 0 10000 0
0 0 0 10000];
H = [1 0 0 0
0 1 0 0
0 0 0 0
0 0 0 0];
I = [1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1];
x = [gy(1)
gx(1)
0
0];
for i = 1:m
pitchMeasure2(i) = atan2(-ax(i),-az(i));
rollMeasure2(i) = atan2(ay(i),-az(i));
F = [1 0 -dt 0
0 1 0 -dt
0 0 1 0
0 0 0 1];
B = [dt 0 0 0
0 dt 0 0
0 0 0 0
0 0 0 0];
u = [gy(i)
gx(i)
0
0];
z = [pitchMeasure2(i)
rollMeasure2(i)
0
0];
%Predicted state estimate
x = F*x + B*u;
%Predicted estimate covariance
P = F*P*F' + dt*Q;
%Measurement residual
y = z - H*x;
%Residual covariance
S = H*P*H' + R;
%Optimal Kalman gain
K = P*H'*pinv(S);
%Updated state estimate
x = x + K*y;
%Updated estimate covariance
P = (I - K*H)*P;
pitchKF2(i) = x(1);
rollKF2(i) = x(2);
bp(i) = x(3);
bq(i) = x(4);
P_out(i,1:4,1:4) = P(1:4,1:4);
end
figure(8)
subplot(211)
plot(t1,rollKF2,t1,roll,'r');title('roll 角度对比');xlabel('Time(s)');grid;
legend('两轴卡尔曼','参考角度')
subplot(212)
plot(t1,pitchKF2,t1,pitch,'r');title('pitch 角度对比');xlabel('Time(s)');grid;
legend('两轴卡尔曼','参考角度')
仿真结果:

目前为止,我们介绍的都是线性模型的姿态估计。以卡尔曼为例,这两种算法基本能满足使用要求,但存在不足。由于线性模型的关系,在只有一个轴向运动的时候,效果还不错,简单来说,比如一个运动同时包含了两个轴,这时候得到的结果就不准确了,上述的一些跟踪不好的地方就是因为此时yaw有运动,所以计算的结果受到了影响。
所以,实际飞行器的运动为非线性模型,我们也要考虑非线性模型的姿态估计。
6、mahony算法
实际在飞控应用时,以上所描述的线性互补很难满足使用要求,因此要求更佳的算法。常见的有mahony,属于非线性互补滤波。算法原理:根据加速度计和地磁计的数据,转换到地理坐标系后,与对应参考的重力向量和地磁向量进行求误差,这个误差用来校正陀螺仪的输出,然后用陀螺仪数据进行四元数更新,再转换到欧拉角。
具体步骤如下:








代码:
%mahony
halfT = 0.5 * dt;
Kp = 0.25;
Ki = 0.0;
exInt = zeros(m,1);
eyInt = zeros(m,1);
ezInt = zeros(m,1);
q0 = zeros(m,1);
q1 = zeros(m,1);
q2 = zeros(m,1);
q3 = zeros(m,1);
q0q0 = zeros(m,1);
q0q1 = zeros(m,1);
q0q2 = zeros(m,1);
q0q3 = zeros(m,1);
q1q1 = zeros(m,1);
q1q2 = zeros(m,1);
q1q3 = zeros(m,1);
q2q2 = zeros(m,1);
q2q3 = zeros(m,1);
q3q3 = zeros(m,1);
q0(1) = 1;
rollmahony = zeros(m,1);
pitchmahony = zeros(m,1);
yawmahony = zeros(m,1);
az = -az;
for i=2:m
q0q0(i)=q0(i-1)*q0(i-1);
q0q1(i)=q0(i-1)*q1(i-1);
q0q2(i)=q0(i-1)*q2(i-1);
q0q3(i)=q0(i-1)*q3(i-1);
q1q1(i)=q1(i-1)*q1(i-1);
q1q2(i)=q1(i-1)*q2(i-1);
q1q3(i)=q1(i-1)*q3(i-1);
q2q2(i)=q2(i-1)*q2(i-1);
q2q3(i)=q2(i-1)*q3(i-1);
q3q3(i)=q3(i-1)*q3(i-1);
norm = sqrt(mx(i)*mx(i)+my(i)*my(i)+mz(i)*mz(i));
mx(i)=mx(i)/norm;
my(i)=my(i)/norm;
mz(i)=mz(i)/norm;
hx = 2.0 * (mx(i) * (0.5 - q2q2(i) - q3q3(i)) + my(i) * (q1q2(i) - q0q3(i)) + mz(i) * (q1q3(i) + q0q2(i)));
hy = 2.0 * (mx(i) * (q1q2(i) + q0q3(i)) + my(i) * (0.5 - q1q1(i) - q3q3(i)) + mz(i) * (q2q3(i) - q0q1(i)));
bx = sqrt(hx * hx + hy * hy);
ez_ef = -hy * bx;
mag_ex = 2.0 * (q1q3(i) - q0q2(i)) * ez_ef;
mag_ey = 2.0 * (q2q3(i) + q0q1(i)) * ez_ef;
mag_ez = (1.0 - 2.0 * q1q1(i) - 2.0 * q2q2(i)) * ez_ef;
norm=sqrt(ax(i)*ax(i)+ay(i)*ay(i)+az(i)*az(i));%把加计的三维向量转成单位向量
ax(i)=ax(i)/norm;
ay(i)=ay(i)/norm;
az(i)=az(i)/norm;
halfex = (ay(i)*(1.0 - 2.0*q1q1(i) - 2.0*q2q2(i)) - az(i)*(2.0*(q2q3(i)+q0q1(i))));
halfey = (az(i)*(2.0*(q1q3(i)-q0q2(i))) - ax(i)*(1.0 - 2.0*q1q1(i) - 2.0*q2q2(i)));
halfez = (ax(i)*(2.0*(q2q3(i)+q0q1(i))) - ay(i)*(2.0*(q1q3(i)-q0q2(i))));
ex = halfex;% + mag_ex;
ey = halfey;% + mag_ey;
ez = halfez;% + mag_ez;
exInt(i) = exInt(i) + ex* Ki* dt;
eyInt(i) = eyInt(i) + ey* Ki* dt;
ezInt(i) = ezInt(i) + ez* Ki* dt;
gx(i) = (gx(i) + Kp*ex + exInt(i))*halfT;
gy(i) = (gy(i) + Kp*ey + eyInt(i))*halfT;
gz(i) = (gz(i) + Kp*ez + ezInt(i))*halfT;
q0(i) = q0(i-1) + (-q1(i-1)*gx(i) - q2(i-1)*gy(i) - q3(i-1)*gz(i));%四元数微分方程
q1(i) = q1(i-1) + ( q0(i-1)*gx(i) + q2(i-1)*gz(i) - q3(i-1)*gy(i));
q2(i) = q2(i-1) + ( q0(i-1)*gy(i) - q1(i-1)*gz(i) + q3(i-1)*gx(i));
q3(i) = q3(i-1) + ( q0(i-1)*gz(i) + q1(i-1)*gy(i) - q2(i-1)*gx(i));
norm = sqrt(q0(i)*q0(i) + q1(i)*q1(i) + q2(i)*q2(i) + q3(i)*q3(i));%四元数规范化
q0(i) = q0(i) / norm;
q1(i) = q1(i) / norm;
q2(i) = q2(i) / norm;
q3(i) = q3(i) / norm;
rollmahony(i) = atan2(2 * q2(i) * q3(i) + 2 * q0(i) * q1(i), -2 * q1(i) * q1(i) - 2 *q2(i)* q2(i) + 1); %roll
pitchmahony(i) = (asin(2 * q0(i) * q2(i) - 2 * q1(i)* q3(i))); % pitch
yawmahony(i) = atan2(2 * q1(i) * q2(i) + 2 * q0(i) * q3(i) , -2 *q2(i) * q2(i) - 2 * q3(i) * q3(i) +1);
end
figure(9)
subplot(311)
plot(t1,rollmahony,t1,roll,'r');title('roll 角度对比');xlabel('Time(s)');grid;
legend('mahony','参考角度')
subplot(312)
plot(t1,pitchmahony,t1,pitch,'r');title('pitch 角度对比');xlabel('Time(s)');grid;
legend('mahony','参考角度')
subplot(313)
plot(t1,yawmahony,t1,yaw,'r');title('yaw 角度对比');xlabel('Time(s)');grid;
legend('mahony','参考角度')
仿真结果:

图中可以看出,算法结果基本能跟踪参考角度,性能较好。实际工程中,我们也常常使用mahony算法进行姿态估计。
7、扩展卡尔曼滤波
由于是非线性模型,所以在卡尔曼的基础上,我们进行改进,采用扩展卡尔曼滤波算法。
模型一:
PX4飞控早期的attitude_estimator_ekf版本。



此为开源代码,读者可自行进行移植测试。如对理论不理解的,可参见视频教程。
模型二:
参考书目
Nonami K, Kendoul F, Suzuki S, et al. Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles[M]. Springer Publishing Company, Incorporated, 2010.
第10章

这里笔者进行了修改,将7状态量缩减成4状态量,只更新四元数。
代码:
p=rollrate;
q=pitchrate;
r=yawrate;
%ACC的测量噪声
var_ax=5;
var_ay=5;
var_az=5;
%mag的测量噪声
var_mx=50;
var_my=50;
var_mz=50;
%状态变量的过程噪声
P1=[1,1,1,1];
P=diag(P1);
x_e=[1;0;0;0];
Pitch = zeros(m,1);
Roll = zeros(m,1);
Yaw = zeros(m,1);
%状态转移矩阵
F = eye(4,4);
%卡尔曼增益矩阵
K = zeros(4,3);
%观测矩阵
H = zeros(3,4);
Hdt=0.5*dt;
Q1 = 0.00001;%Q矩阵中的数也是经验值得到,需要在考虑q中的参数
Q2 = 0.01;
R=zeros(6,6);
R(1,1)=var_ax;
R(2,2)=var_ay;
R(3,3)=var_az;
R(4,4)=var_mx;
R(5,5)=var_my;
R(6,6)=var_mz;
% R=zeros(3,3);
% R(1,1)=var_ax;
% R(2,2)=var_ay;
% R(3,3)=var_az;
for i=1:m
norm = 1.0/sqrt(x_e(1,1)*x_e(1,1)+x_e(2,1)*x_e(2,1)+x_e(3,1)*x_e(3,1)+x_e(4,1)*x_e(4,1));
for n=1:4
x_e(n,1)=x_e(n,1)*norm;
end
%状态转移矩阵
F = [ 1, -Hdt*(p(i)), -Hdt*(q(i)), -Hdt*(r(i));
Hdt*(p(i)), 1, Hdt*(r(i)), -Hdt*(q(i));
Hdt*(q(i)), -Hdt*(r(i)), 1, Hdt*(p(i));
Hdt*(r(i)), Hdt*(q(i)), -Hdt*(p(i)), 1;];
dTemp(1)=x_e(1,1)-Hdt*(p(i))*x_e(2,1)-Hdt*(q(i))*x_e(3,1)-Hdt*(r(i))*x_e(4,1);
dTemp(2)=x_e(2,1)+Hdt*(p(i))*x_e(1,1)-Hdt*(q(i))*x_e(4,1)+Hdt*(r(i))*x_e(3,1);
dTemp(3)=x_e(3,1)+Hdt*(p(i))*x_e(4,1)+Hdt*(q(i))*x_e(1,1)-Hdt*(r(i))*x_e(2,1);
dTemp(4)=x_e(4,1)-Hdt*(p(i))*x_e(3,1)+Hdt*(q(i))*x_e(2,1)+Hdt*(r(i))*x_e(1,1);
for j=1:4
x_e(j,1)=dTemp(j);
end
%协方差一步预测更新
P=F*P*F';
%加入噪音项
P(1,1)=P(1,1)+Q1;
P(2,2)=P(2,2)+Q1;
P(3,3)=P(3,3)+Q1;
P(4,4)=P(4,4)+Q1;
y(1,1)= -2.0*(x_e(2,1)*x_e(4,1)-x_e(1,1)*x_e(3,1));
y(2,1)= -2.0*(x_e(1,1)*x_e(2,1)+x_e(3,1)*x_e(4,1));
y(3,1)= -(x_e(1,1)*x_e(1,1)-x_e(2,1)*x_e(2,1)-x_e(3,1)*x_e(3,1)+x_e(4,1)*x_e(4,1));
%测量的Acc数据
norm=sqrt(ax(i)*ax(i)+ay(i)*ay(i)+az(i)*az(i));%把加计的三维向量转成单位向量
ax(i)=ax(i)/norm;
ay(i)=ay(i)/norm;
az(i)=az(i)/norm;
y_s(1,1) = -ax(i);
y_s(2,1) = -ay(i);
y_s(3,1) = az(i);
norm = sqrt(mx(i)*mx(i)+my(i)*my(i)+mz(i)*mz(i));
mx(i)=mx(i)/norm;
my(i)=my(i)/norm;
mz(i)=mz(i)/norm;
y_s(4,1) = mx(i);
y_s(5,1) = my(i);
y_s(6,1) = mz(i);
hx = 2.0 * (mx(i) * (0.5 - x_e(3,1)*x_e(3,1) - x_e(4,1)*x_e(4,1)) + my(i) * (x_e(2,1)*x_e(3,1) - x_e(1,1)*x_e(4,1)) + mz(i) * (x_e(2,1)*x_e(4,1) + x_e(1,1)*x_e(3,1)));
hy = 2.0 * (mx(i) * (x_e(2,1)*x_e(3,1) + x_e(1,1)*x_e(4,1)) + my(i) * (0.5 - x_e(2,1)*x_e(2,1) - x_e(4,1)*x_e(4,1)) + mz(i) * (x_e(3,1)*x_e(4,1) - x_e(1,1)*x_e(2,1)));
bx = sqrt(hx * hx + hy * hy);
bz = 2.0 * (mx(i) * (x_e(2,1)*x_e(4,1) - x_e(1,1)*x_e(3,1)) + my(i) * (x_e(3,1)*x_e(4,1) + x_e(1,1)*x_e(2,1)) + mz(i) * (0.5 - x_e(2,1)*x_e(2,1) - x_e(3,1)*x_e(3,1)));
y(4,1)=bx*(x_e(1,1)*x_e(1,1) + x_e(2,1)*x_e(2,1) - x_e(3,1)*x_e(3,1) - x_e(4,1)*x_e(4,1)) + 2*bz*(x_e(2,1)*x_e(4,1) - x_e(1,1)*x_e(3,1));
y(5,1)=2*bx*(x_e(2,1)*x_e(3,1) - x_e(1,1)*x_e(4,1)) + 2*bz*(x_e(3,1)*x_e(4,1) + x_e(1,1)*x_e(2,1));
y(6,1)=2*bx*(x_e(2,1)*x_e(4,1) + x_e(1,1)*x_e(3,1)) + bz*(x_e(1,1)*x_e(1,1) - x_e(2,1)*x_e(2,1) - x_e(3,1)*x_e(3,1) + x_e(4,1)*x_e(4,1));
%观测矩阵更新
% H = [ 2.0*x_e(3,1), -2.0*x_e(4,1), 2.0*x_e(1,1), -2.0*x_e(2,1);
% -2.0*x_e(2,1), -2.0*x_e(1,1), -2.0*x_e(4,1), -2.0*x_e(3,1);
% -2.0*x_e(1,1), 2.0*x_e(2,1), 2.0*x_e(3,1), -2.0*x_e(4,1);];
H = [ 2*x_e(3,1), -2*x_e(4,1), 2*x_e(1,1), -2*x_e(2,1);
-2*x_e(2,1), -2*x_e(1,1), -2*x_e(4,1), -2*x_e(3,1);
-2*x_e(1,1), 2*x_e(2,1), 2*x_e(3,1), -2*x_e(4,1);
2*( x_e(1,1)*bx - x_e(3,1)*bz), 2*( x_e(2,1)*bx + x_e(4,1)*bz), 2*(-x_e(3,1)*bx - x_e(1,1)*bz), 2*(-x_e(4,1)*bx + x_e(2,1)*bz);
2*(-x_e(4,1)*bx + x_e(2,1)*bz), 2*( x_e(3,1)*bx + x_e(1,1)*bz), 2*( x_e(2,1)*bx + x_e(4,1)*bz), 2*(-x_e(1,1)*bx + x_e(3,1)*bz);
2*( x_e(3,1)*bx + x_e(1,1)*bz), 2*( x_e(4,1)*bx - x_e(2,1)*bz), 2*( x_e(1,1)*bx - x_e(3,1)*bz), 2*( x_e(2,1)*bx + x_e(4,1)*bz)];
%计算卡尔曼增益
K=P*H'*pinv(H*P*H'+R);
%状态估计
x_e=x_e+K*(y_s-y);
%x_e=x_e;
P=P-K*H*P;
norm = 1.0/sqrt(x_e(1,1)*x_e(1,1)+x_e(2,1)*x_e(2,1)+x_e(3,1)*x_e(3,1)+x_e(4,1)*x_e(4,1));
for n=1:4
x_e(n,1)=x_e(n,1)*norm;
end
%四元数转欧拉角
Pitch(i) = asin(2*(x_e(1,1)*x_e(3,1)- x_e(2,1)*x_e(4,1)));
Roll(i) = atan2(2*(x_e(1,1)*x_e(2,1)+x_e(3,1)*x_e(4,1)),1-2*(x_e(2,1)*x_e(2,1)+x_e(3,1)*x_e(3,1)));
Yaw(i) = atan2(2*(x_e(2,1)*x_e(3,1)+x_e(1,1)*x_e(4,1)),1-2*(x_e(3,1)*x_e(3,1)+x_e(4,1)*x_e(4,1)));
end
figure(11)
subplot(311)
plot(t1,Roll,t1,roll,'r');title('roll 角度对比');xlabel('Time(s)');grid;
legend('EKF','参考角度')
subplot(312)
plot(t1,Pitch,t1,pitch ,'r');title('pitch 角度对比');xlabel('Time(s)');grid;
legend('EKF','参考角度')
subplot(313)
plot(t1,Yaw,t1,yaw,'r');title('yaw 角度对比');xlabel('Time(s)');grid;
legend('EKF','参考角度')仿真结果:

Yaw部分是因为参考角度去掉了偏移,只有相对角度,所以实际是正确的跟踪。上图表明,EKF能达到较好的效果,满足使用要求。
至此,我们已经总结了在姿态估计中常用的几种算法,每个算法的不足与优点也大概介绍了。实际在应用时,并不一定是理论越复杂就一定好用,比如EKF,如果模型维数过多,则计算量大大增加,且增加了算法发散的风险,所以工程应用,只选用满足要求的最佳算法。
总结一下:
1、 坐标系对应是姿态估计非常重要的一环,特别是移植;
2、 如何调参?
工程上进行算法开发时,笔者建议的流程是先分析问题,选用相应的算法,并进行设计,取飞行数据,然后在matlab仿真环境下进行仿真调试,最后转换成嵌入式代码实现功能。这样做的好处是,如果在嵌入式环境下进行大量的调参时,非常繁琐,不方便以及不直观。当然,现在有基于模型的开发方式,这里不做过多叙述。具体如何调参,可参见视频教程;
3、 工程应用时,要考虑震动对数据以及算法的影响,动加速度对重力参考的影响,外界地磁干扰对地磁参考的影响,如何在算法中避免这些情况,或者说出现这些情况下如何保证算法不崩溃,即鲁棒性;
4、 没有绝对的最好的算法理论,如何使用,达到最佳效果往往是算法工程师要做的;
5、如果想更多的了解状态估计的理论知识,可参考等其他资料。