shap-Basic SHAP Interaction Value Example in XGBoost

news2024/12/28 21:42:56

Basic SHAP Interaction Value Example in XGBoost

  • XGBoost中的基本SHAP交互值示例
  • 解释没有交互的线性函数
  • SHAP交互值
  • 用一次交互解释线性模型
  • SHAP交互值

用到的环境是python3.7（基于上一篇文章的环境），然后再装了xgboost和shap，没报什么错，挺顺利。。。

conda install xgboost

conda install shap

官方的代码在https://github.com/shap/shap/blob/master/notebooks/tabular_examples/tree_based_models/Basic%20SHAP%20Interaction%20Value%20Example%20in%20XGBoost.ipynb

XGBoost中的基本SHAP交互值示例

这个notebook展示了如何计算一个非常简单的函数的SHAP交互值。我们从一个简单的线性函数开始，然后添加一个交互项，看看它如何改变SHAP值和SHAP交互值。

SHAP值（Shapley Additive exPlanations）的主要思想就是Shapley值，Shapley值是一个来自合作博弈论（coalitional game theory）的方法，由Shapley在1953年创造的Shapley值是一种根据玩家对总支出的贡献来为玩家分配支出的方法，玩家在联盟中合作并从这种合作中获得一定的收益。用shaply值去解释机器学习的预测的话，其中“总支出”就是数据集单个实例的模型预测值，“玩家”是实例的特征值，“收益”是该实例的实际预测减去所有实例的平均预测。

一个简单模型（如线性回归）的最好解释是模型本身，它们容易理解。对于复杂的模型（如集成模型或深度学习模型），它们是不容易理解的，我们不能使用原始模型本身去作为它的解释，相反，我们必须使用一个简单的解释模型，我们将其定义为原始模型的任意解释逼近。SHAP将Shapley值解释表示为一种可加特征归因方法，SHAP将模型的预测值解释为每个输入特征的归因值之和。

当前的归因方法不能直接表示相互作用，但必须在每个特征之间划分相互作用的影响。为了直接捕捉成对的相互作用效果，我们基于博弈论中Shapley交互指数扩展SHAP值，提出了SHAP交互值（SHAP INTERACTION VALUES），SHAP交互值保证了一致性的同时可以解释单个预测的交互效果。

特征归因通常在输入特征之间分配，每个特征分配一个归因值，但是我们可以通过将交互效果与主要效果分离来获得额外的信息。如果我们考虑成对的相互作用，就会得到一个属性值矩阵，表示所有的两个特征对给定模型预测的影响。由于SHAP值是基于博弈论中的经典Shapley值，所以通过更现代的Shapley交互指标可以得到对交互效果的自然扩展。

import xgboost
import numpy as np
import shap

有一点警告提示，没啥影响，问题不大，忽略。

C:\Users\gxx\anaconda3\envs\tf-py37\lib\site-packages\tqdm\auto.py:22: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

解释没有交互的线性函数

# simulate some binary data and a linear outcome with an interaction term
# note we make the features in X perfectly independent of each other to make
# it easy to solve for the exact SHAP values
N = 2000
X = np.zeros((N,5))
X[:1000,0] = 1
X[:500,1] = 1
X[1000:1500,1] = 1
X[:250,2] = 1
X[500:750,2] = 1
X[1000:1250,2] = 1
X[1500:1750,2] = 1
X[:,0:3] -= 0.5
y = 2*X[:,0] - 3*X[:,1]

# ensure the variables are independent
np.cov(X.T)

输出结果：

array([[0.25012506, 0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.25012506, 0.        , 0.        , 0.        ],
       [0.        , 0.        , 0.25012506, 0.        , 0.        ],
       [0.        , 0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.        , 0.        , 0.        , 0.        ]])

# and mean centered
X.mean(0)

输出结果：

array([0., 0., 0., 0., 0.])

# train a model with single tree
Xd = xgboost.DMatrix(X, label=y)
model = xgboost.train({
    'eta':1, 'max_depth':3, 'base_score': 0, "lambda": 0
}, Xd, 1)
print("Model error =", np.linalg.norm(y-model.predict(Xd)))
print(model.get_dump(with_stats=True)[0])

输出结果：

Model error = 0.0
0:[f1<0] yes=1,no=2,missing=1,gain=4500,cover=2000
	1:[f0<0] yes=3,no=4,missing=3,gain=1000,cover=1000
		3:leaf=0.5,cover=500
		4:leaf=2.5,cover=500
	2:[f0<0] yes=5,no=6,missing=5,gain=1000,cover=1000
		5:leaf=-2.5,cover=500
		6:leaf=-0.5,cover=500

# make sure the SHAP values add up to marginal predictions
pred = model.predict(Xd, output_margin=True)
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(Xd)
np.abs(shap_values.sum(1) + explainer.expected_value - pred).max()

输出结果：

0.0

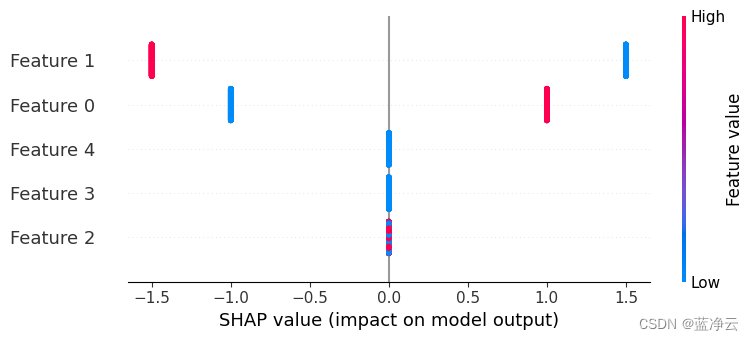
如果我们建立一个汇总图，我们可以看到只有特征1和2有任何影响，并且它们的影响只有两个可能的大小（一个为-0.5，一个为0.5）。

shap.summary_plot(shap_values, X)

输出结果：
在这里插入图片描述

# train a linear model
from sklearn import linear_model
lr = linear_model.LinearRegression()
lr.fit(X, y)
lr_pred = lr.predict(X)
lr.coef_.round(2)

输出结果：

array([ 2., -3.,  0.,  0.,  0.])

# Make sure the computed SHAP values match the true SHAP values
# (we can compute the true SHAP values directly for this simple case)
main_effect_shap_values = lr.coef_ * (X - X.mean(0))
np.linalg.norm(shap_values - main_effect_shap_values)

输出结果：

2.1980906908667245e-13

SHAP交互值

注意，当不存在交互作用时，SHAP交互作用值只是对角线上的SHAP值的对角线矩阵。

shap_interaction_values = explainer.shap_interaction_values(Xd)
shap_interaction_values[0]

输出结果：

array([[ 1. ,  0. ,  0. ,  0. ,  0. ],
       [ 0. , -1.5,  0. ,  0. ,  0. ],
       [ 0. ,  0. ,  0. ,  0. ,  0. ],
       [ 0. ,  0. ,  0. ,  0. ,  0. ],
       [ 0. ,  0. ,  0. ,  0. ,  0. ]], dtype=float32)

# ensure the SHAP interaction values sum to the marginal predictions
np.abs(shap_interaction_values.sum((1,2)) + explainer.expected_value - pred).max()

输出结果：

0.0

# ensure the main effects from the SHAP interaction values match those from a linear model
dinds = np.diag_indices(shap_interaction_values.shape[1])
total = 0
for i in range(N):
    for j in range(5):
        total += np.abs(shap_interaction_values[i,j,j] - main_effect_shap_values[i,j])
total

输出结果：

1.3590530773134374e-11

用一次交互解释线性模型

# simulate some binary data and a linear outcome with an interaction term
# note we make the features in X perfectly independent of each other to make
# it easy to solve for the exact SHAP values
N = 2000
X = np.zeros((N,5))
X[:1000,0] = 1

X[:500,1] = 1
X[1000:1500,1] = 1

X[:250,2] = 1
X[500:750,2] = 1
X[1000:1250,2] = 1
X[1500:1750,2] = 1

X[:125,3] = 1
X[250:375,3] = 1
X[500:625,3] = 1
X[750:875,3] = 1
X[1000:1125,3] = 1
X[1250:1375,3] = 1
X[1500:1625,3] = 1
X[1750:1875,3] = 1
X[:,:4] -= 0.4999 # we can't exactly mean center the data or XGBoost has trouble finding the splits
y = 2* X[:,0] - 3 * X[:,1] + 2 * X[:,1] * X[:,2]

X.mean(0)

输出结果：

array([1.e-04, 1.e-04, 1.e-04, 1.e-04, 0.e+00])

# train a model with single tree
Xd = xgboost.DMatrix(X, label=y)
model = xgboost.train({
    'eta':1, 'max_depth':4, 'base_score': 0, "lambda": 0
}, Xd, 1)
print("Model error =", np.linalg.norm(y-model.predict(Xd)))
print(model.get_dump(with_stats=True)[0])

输出结果：

Model error = 1.73650378306776e-06
0:[f1<0.000100001693] yes=1,no=2,missing=1,gain=4499.40039,cover=2000
	1:[f0<0.000100001693] yes=3,no=4,missing=3,gain=999.999756,cover=1000
		3:[f2<0.000100001693] yes=7,no=8,missing=7,gain=124.949997,cover=500
			7:leaf=0.99970001,cover=250
			8:leaf=-9.99800031e-05,cover=250
		4:[f2<0.000100001693] yes=9,no=10,missing=9,gain=124.949951,cover=500
			9:leaf=2.99970007,cover=250
			10:leaf=1.99989998,cover=250
	2:[f0<0.000100001693] yes=5,no=6,missing=5,gain=999.999756,cover=1000
		5:[f2<0.000100001693] yes=11,no=12,missing=11,gain=125.050049,cover=500
			11:leaf=-3.0000999,cover=250
			12:leaf=-1.99989998,cover=250
		6:[f2<0.000100001693] yes=13,no=14,missing=13,gain=125.050018,cover=500
			13:leaf=-1.00010002,cover=250
			14:leaf=0.000100019999,cover=250

# make sure the SHAP values add up to marginal predictions
pred = model.predict(Xd, output_margin=True)
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(Xd)
np.abs(shap_values.sum(1) + explainer.expected_value - pred).max()

输出结果：

4.7683716e-07

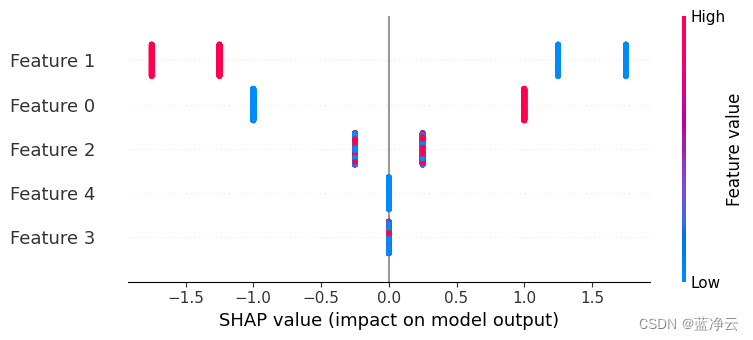
如果我们构建一个总结图，我们会发现现在只有功能3和4无关紧要，而功能1可能由于交互而具有四种可能的效果大小。

shap.summary_plot(shap_values, X)

输出结果：
在这里插入图片描述

# train a linear model
lr = linear_model.LinearRegression()
lr.fit(X, y)
lr_pred = lr.predict(X)
lr.coef_.round(2)

输出结果：

array([ 2., -3.,  0.,  0.,  0.])

# Note that the SHAP values no longer match the main effects because they now include interaction effects
main_effect_shap_values = lr.coef_ * (X - X.mean(0))
np.linalg.norm(shap_values - main_effect_shap_values)

输出结果：

15.811387829626847

SHAP交互值

# SHAP interaction contributions:
shap_interaction_values = explainer.shap_interaction_values(Xd)
shap_interaction_values[0].round(2)

输出结果：

array([[ 1.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  , -1.5 ,  0.25,  0.  ,  0.  ],
       [ 0.  ,  0.25,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ]], dtype=float32)

# ensure the SHAP interaction values sum to the marginal predictions
np.abs(shap_interaction_values.sum((1,2)) + explainer.expected_value - pred).max()

输出结果：

4.7683716e-07

# ensure the main effects from the SHAP interaction values match those from a linear model.
# while the main effects no longer match the SHAP values when interactions are present, they do match
# the main effects on the diagonal of the SHAP interaction value matrix
dinds = np.diag_indices(shap_interaction_values.shape[1])
total = 0
for i in range(N):
    for j in range(5):
        total += np.abs(shap_interaction_values[i,j,j] - main_effect_shap_values[i,j])
total

输出结果：

0.0005347490550661898

如果我们为特征0构建依赖图，我们会发现它只需要两个值，并且这些值完全取决于特征的值（特征0的值完全决定了它的效果，因为它与其他特征没有交互）。

shap.dependence_plot(0, shap_values, X)

输出结果：
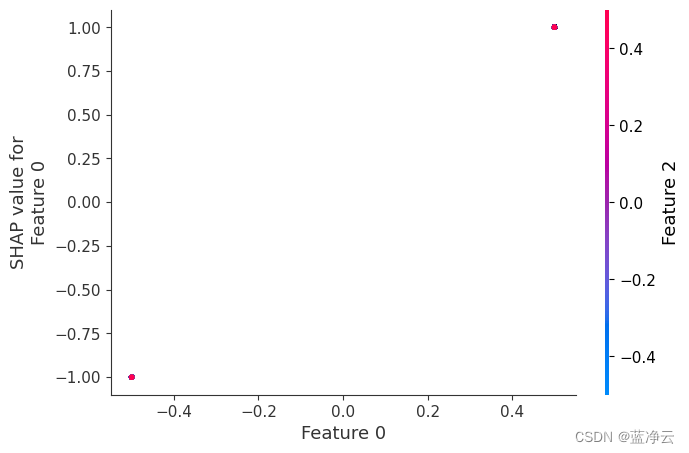
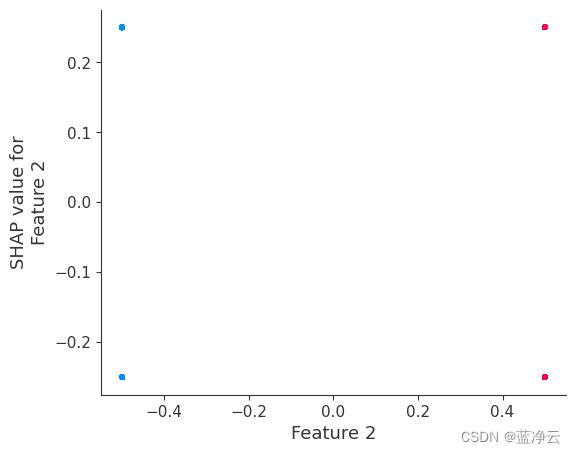
在这里插入图片描述
相反，如果我们为特征2建立依赖图，我们会看到它采用了4个可能的值，并且它们并不完全由特征2的值决定，相反，它们也取决于特征3的值。相关性图中的这种垂直分布表示非线性相互作用的影响。

shap.dependence_plot(2, shap_values, X)

警告： invalid value encountered in true_divide invalid value encountered in true_divide
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1038579.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

GIT 提交过滤非必要文件

GIT 提交过滤非必要文件

1、git ls-files&#xff1a;该命令会列出Git仓库中管理的所有文件 2、git rm -r -f --cached . -f 是强制删除 最后的点 是删除所有 git rm -r --cached . 3、 进入Preferences->plugins 中下载一个(.ignore)插件　　在项目本地new一个(.gitignore)的文件新增需要过滤文…
阅读更多...
最全跨境独立站建站详细步骤解析

最全跨境独立站建站详细步骤解析

对于跨境电商卖家来说&#xff0c;无论是规避“鸡蛋放在同一个篮子里”的风险&#xff0c;还是追求更多的销售额和利润&#xff0c;多平台、多站点的布局都是其至关重要的战略。加之市场的变化带来了新的发展机遇&#xff0c;这也使得如今很多出海企业都在抢占独立站新风口。然…
阅读更多...
四、线性支持向量机算法(LinearSVC，Linear Support Vector Classification)（有监督学习）

四、线性支持向量机算法(LinearSVC，Linear Support Vector Classification)（有监督学习）

线性支持向量机&#xff0c;Linear Support Vector Classification. 与参数内核为线性的SVC类似(SVC(kernel‘linear’))&#xff0c;但使用liblinear而非libsvm实现&#xff0c;因此在选择惩罚和损失函数时更具灵活性&#xff0c;并能更好地扩展到大量样本 SVC(kernel’linea…
阅读更多...
【沐风老师】3DMAX路径拖尾光线刀光效果插件GhostTrails教程

【沐风老师】3DMAX路径拖尾光线刀光效果插件GhostTrails教程

3DMAX路径拖尾光线刀光效果插件GhostTrails&#xff0c;是3dsmax的动画挤出修改器。它非常适合风格化的运动模糊效果、轮胎轨迹、Tron光循环和许多其他用途。 【适用版本】 3dMax2010 - 2024 【安装方法】 1.将对应版本的GhostTrails 插件复制到 3dmax 插件目录&#xff08;如…
阅读更多...
原创动画《优弧，你小子！》

原创动画《优弧，你小子！》

&#x1f4a5; 背景 体验效果直接翻到第三章&#xff1a;成果体验 先来介绍一下优弧&#xff1a;掘金平台管理员丨首席客服君丨运营负责人 &#x1f468;‍✈️ 现在优弧到底是妹子还是汉子仍是一个未解之谜&#xff0c;网上众说纷纭。他说&#xff1a;优弧是个200来斤的胖子&a…
阅读更多...
AIGC赋能甄知燕千云员工AI助手，升级企业智创之旅

AIGC赋能甄知燕千云员工AI助手，升级企业智创之旅

燕千云数智化业务服务平台发布了1.24.0版本&#xff0c;此次版本升级了燕千云智能工单&#xff0c;增加了一键外呼功能&#xff0c;并且优化了在线客服接入了失败通知&#xff0c;满足不同的用户需求&#xff0c;此次还升级了智能助理&#xff0c;知识中心等功能&#xff0c;满…
阅读更多...
[计算机入门] Windows附件程序介绍(影音类)

[计算机入门] Windows附件程序介绍(影音类)

3.12 附件程序介绍(影音类) 3.12.1 附件程序介绍 附件程序是在安装完Windows系统后&#xff0c;系统自带的一些非常常用且重要的软件程序。可以通过下面的方式搜索并打开附件程序(以打开画图程序为例)&#xff1a; 1、点击左下角windows菜单&#xff1a; 2、直接输入要打开…
阅读更多...
基于 SpringBoot+Vue的电影影城管理系统，附源码，数据库

基于 SpringBoot+Vue的电影影城管理系统，附源码，数据库

文章目录 第一章 简介第二章 技术栈第三章 功能分析第四章 系统设计第5章 系统详细设计六 源码咨询 第一章 简介 本影城管理系统&#xff0c;是基于 Java SpringBoot 开发的。主要包括二大功能模块&#xff0c;即用户功能模块和管理员功能模块。 &#xff08;1&#xff09;管…
阅读更多...
在win系统安装部署svn服务及客户端使用

在win系统安装部署svn服务及客户端使用

1. 安装svn服务端 1.1. 下载svn服务端 进入SVN服务端官网&#xff0c;并下载&#xff1a; 1.2. 下载后双击即可安装&#xff0c;选择下一步 1.3. 同意许可&#xff0c;选择下一步 1.4. 选择安装SVN的组件&#xff0c;默认&#xff0c;下一步 1.5. 设置安装路径、仓库路径、…
阅读更多...
Python爬虫实战：用简单四步爬取小红书图片

Python爬虫实战：用简单四步爬取小红书图片

小红书是一个热门的社交分享平台&#xff0c;汇聚了大量精美的图片。如果您希望保存或使用这些图片&#xff0c;本文将为您详细介绍如何使用Python爬虫轻松爬取小红书图片。 一、安装必要的库 在开始之前&#xff0c;确保您已经安装了以下Python库&#xff1a; requests&#…
阅读更多...
http的get与post

http的get与post

get方法&#xff1a; 这个网址可以获取配置信息&#xff08;我把部分位置字符改了&#xff0c;现在打不开了&#xff0c;不然会被追责&#xff09; http://softapi.s103.cn/addons/Kmdsoft/Index/config?productwxdk&partner_id111122&osWindows&os_version11&am…
阅读更多...
Nginx之QPS限制模块解读

Nginx之QPS限制模块解读

目录 基本介绍 模块配置具体解读 limit_req_zone limit_req 原理&#xff1a;漏桶算法 基本介绍 NGINX通过limit_req_zone和limit_req两条指令来实现速率限制。指令limit_req_zone定义了限速的参数&#xff0c;指令limit_req在所在的location使能定义的速率。 QPS即每秒…
阅读更多...
ChatGPT AIGC 非常实用的AI工具集合大全

ChatGPT AIGC 非常实用的AI工具集合大全

实战AI 工具箱 AIGC ChatGPT 职场案例60集， Power BI 商业智能 68集， 数据库Mysql8.0 54集 数据库Oracle21C 142集， Office， Python ，ETL Excel 2021 实操，函数，图表，大屏可视化 案例实战 http://t.csdn.cn/zBytu
阅读更多...
工厂进销存软件怎么选？

工厂进销存软件怎么选？

本文将为大家讲解&#xff1a;工厂进销存软件怎么选&#xff1f; 工厂的进销存管理对于生产和供应链的顺畅运作至关重要。为了更好地管理库存、优化生产和确保及时交货&#xff0c;工厂需要选择一款合适的进销存软件。本文将介绍工厂应该考虑的关键因素&#xff0c;以帮助他们…
阅读更多...
统一系统脆弱性管理平台：让“网络安全漏洞”无处遁形

统一系统脆弱性管理平台：让“网络安全漏洞”无处遁形

网络安全漏洞是网络节点的系统软件或应用软件在逻辑设计上的缺陷&#xff0c;漏洞是在硬件、软件、协议的具体实现或系统安全策略上存在的缺陷&#xff0c;从而可以使网络攻击者能够在未授权的情况下访问或破坏系统。 网络安全漏洞被利用了&#xff0c;危害极大。正是因为如此&…
阅读更多...
华为云云耀云服务器L实例评测 | Docker 部署 Reids容器

华为云云耀云服务器L实例评测 | Docker 部署 Reids容器

文章目录 一、使用Docker部署的好处二、Docker 与 Kubernetes 对比三、云耀云服务器L实例 Docker 部署 Redis四、可视化工具连接Redis⛵小结 一、使用Docker部署的好处 Docker的好处在于&#xff1a;在不同实例上运行相同的容器 Docker的五大优点&#xff1a; 持续部署与测试…
阅读更多...
电脑C盘爆红怎么办？（小白篇）

电脑C盘爆红怎么办？（小白篇）

文章目录 前言&#xff1a;1、清理临时和系统文件2、更改电脑默认软件安装位置3、微信、QQ文件存储路径放在其它盘4、卸载一些不常用的软件彩蛋 前言&#xff1a; C盘作为电脑的系统盘&#xff0c;如果出现爆满或者剩余空间很小整个C盘变红&#xff0c;这样会导致电脑系统运行…
阅读更多...
二次号查询API：检测手机号是否二次入网，提高用户信任度

二次号查询API：检测手机号是否二次入网，提高用户信任度

引言 在数字时代&#xff0c;个人数据的安全和隐私保护变得至关重要。用户信任是在线业务成功的基石&#xff0c;而其中一个关键方面是保护用户的个人信息不受滥用和侵犯。为了增强用户信任度&#xff0c;越来越多的企业和服务提供商正在采用手机号是否二次入网检测API&#x…
阅读更多...
Java对象内存图

Java对象内存图

对象内存图
阅读更多...
【湖科大教书匠】计算机网络随堂笔记第4章（计算机网络网络层）

【湖科大教书匠】计算机网络随堂笔记第4章（计算机网络网络层）

目录 4.1、网络层概述 简介 要实现网络层任务&#xff0c;需要解决一下主要问题&#xff1a; 网络层向运输层提供怎样的服务&#xff08;“可靠传输”还是“不可靠传输”&#xff09; 网络层寻址问题 路由选择问题 路由器收到数据后&#xff0c;是依据什么来决定将数据包从自己…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023