多卫星定位算法

现已知有N(N>=4)个卫星，每个卫星的坐标用$X_s$表示，其对应的伪距用$r$表示。
由于伪距不是准确的、真实的距离，它有所干扰。所以我们可以再根据三维空间中的距离公式，另外估计卫星和用户的距离为$\hat{r}$。公式如下：
$$\hat{r}=F\left(X\right)+c\delta t$$
此时注意此时的$X$和$X_s$都是三维矢量(vector)，$X$表示用户的坐标。
$$X=\left(\begin{array}{l}x\\ y\\ z\end{array}\right)$$
其中$c$是光速$(m/s)$，$\delta t$是卫星和接收机的时间差。$F\left(X\right)$的距离公式如下：
$$F\left(X\right)={\left({\left(x-x_s\right)}^2+{\left(y-y_s\right)}^2+{\left(z-z_s\right)}^2\right)}^{1/2}$$
对$F\left(X\right)$泰勒展开（Taylor Expansion）：
$$F\left(X\right)=F\left(X_0\right)+\frac{dF\left(X_0\right)}{dX}\left(X-X_0\right)+o\left(X\right)$$
再对$\frac{dF\left(X_0\right)}{dX}\left(X-X_0\right)$进行多元展开：
$$\begin{array}{l}\frac{dF\left(X_0\right)}{dX}\left(X-X_0\right)=\frac{\partial {\left({\left(x-x_s\right)}^2+{\left(y-y_s\right)}^2+{\left(z-z_s\right)}^2\right)}^{1/2}}{\partial x}{|}_{x=x_0}\left(x-x_0\right)+\frac{\partial {\left({\left(x-x_s\right)}^2+{\left(y-y_s\right)}^2+{\left(z-z_s\right)}^2\right)}^{1/2}}{\partial y}{|}_{y=y_0}\left(y-y_0\right)+\frac{\partial {\left({\left(x-x_s\right)}^2+{\left(y-y_s\right)}^2+{\left(z-z_s\right)}^2\right)}^{1/2}}{\partial z}{|}_{z=z_0}\left(z-z_0\right)\\ \\ =\frac{x_0-x_s}{F\left(X_0\right)}\left(x-x_0\right)+\frac{y_0-y_s}{F\left(X_0\right)}\left(y-y_0\right)+\frac{z_0-z_s}{F\left(X_0\right)}\left(z-z_0\right)\\ \\ =\frac{x_0-x_s}{F\left(X_0\right)}\delta x+\frac{y_0-y_s}{F\left(X_0\right)}\delta y+\frac{z_0-z_s}{F\left(X_0\right)}\delta z\end{array}$$
忽略泰勒展开的高阶项之后，再将以上的等式矩阵化得到：

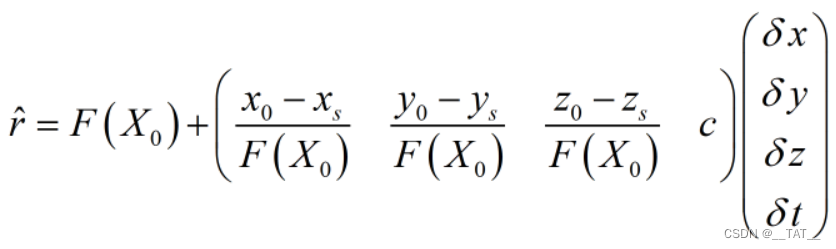
以上只是对于一个卫星而言，如果拓展多个卫星就得到：

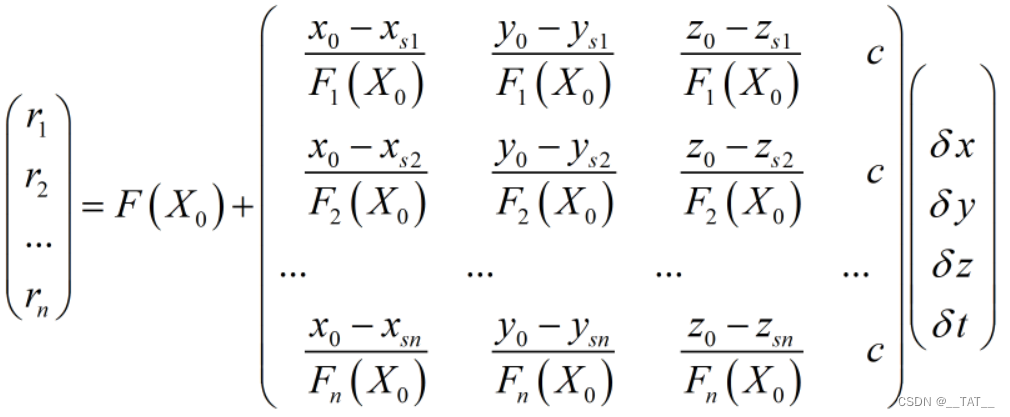
令其等于$\hat{R}=A\delta X$。
再根据最小二乘法的公式：
$$L\left(X\right)={\Vert \hat{R}-R\Vert }^2$$
得到：
$$\begin{array}{l}L\left(\delta X\right)={\Vert A\delta X-\left(R-F\left(X_0\right)\right)\Vert }^2\\ \\ =\delta X^T{A}^{T}A\delta X-2{\left(R-F\left(X_0\right)\right)}^{T}A\delta X+{\left(R-F\left(X_0\right)\right)}^T\left(R-F\left(X_0\right)\right)\end{array}$$
对$\delta X$推导出以下公式：
$$\begin{array}{l}\delta X={\left(A^{T}A\right)}^{-1}{A}^T\left(R-F\left(X_0\right)\right)\\ \\ X=X_0+\delta X\end{array}$$
最后，由于泰勒展开时$X_0$是任意取的，所以我们并不能确定它就是$X$附近，而如果$X_0$不在$X$附近，再忽略掉泰勒展开后高阶项将导致巨大的误差。为了解决这个问题，我们将计算得到的$X$当成$X_0$循环代入以上这些公式，直到本次得到$X$值和上次得到$X$差别不大，才跳出循环。