---

前言

---

提示：生活就是一场有很多规则，却没有裁判的比赛。 --约瑟夫·布罗茨基《悲伤与理智》

最近公共祖先问题

参考题目地址：236. 二叉树的最近公共祖先 - 力扣（LeetCode）

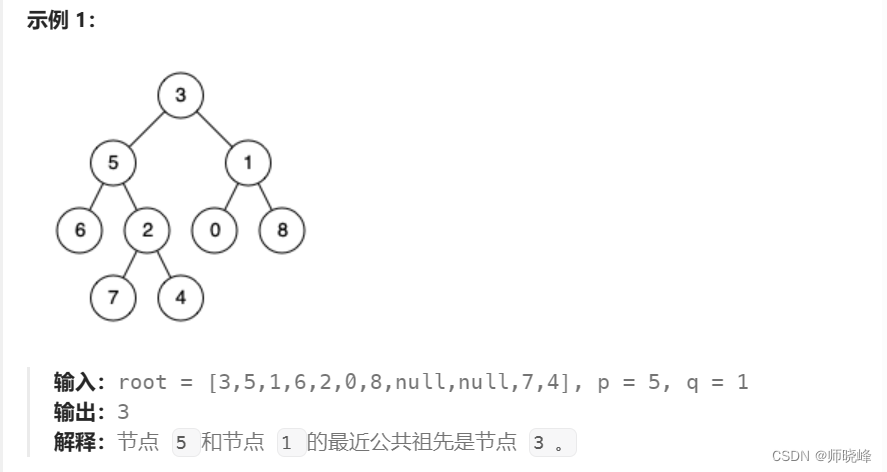
如果将搜索二叉树换成普通的二叉树该怎么做呢？该怎么做呢？

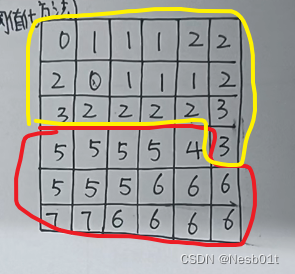
要想找到两个节点的最进公共祖先节点，我们可以从两个节点往上找，每个节点都往上走，一直走到根节点，那么根节点到这两个节点的连线肯定有相关的地方，如果是从上面往下走，那么最后一次相交的节点就是他们的最近公共公祖先节点。我们就可以找到6和7的最近公共节点画一个图看下：

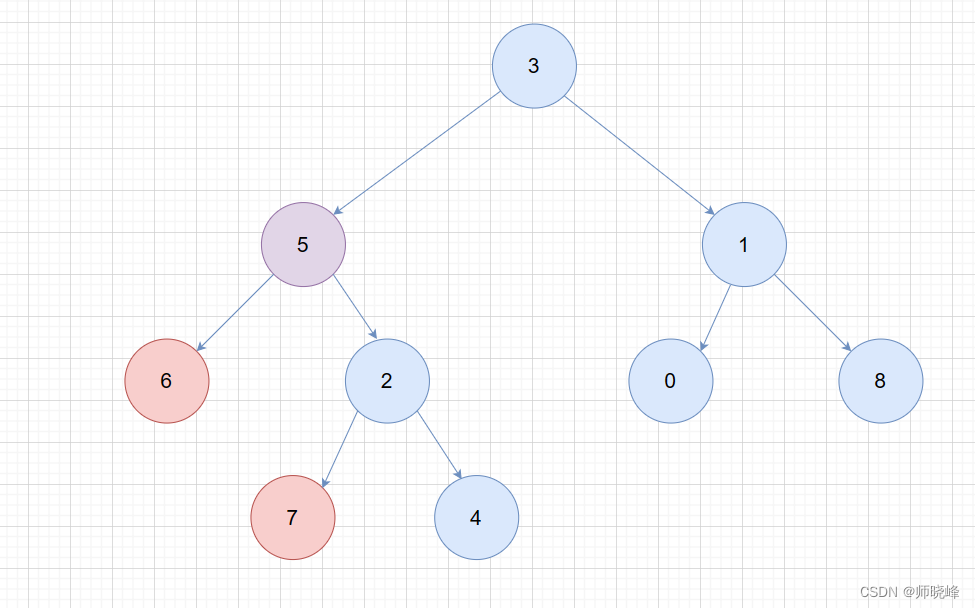
6的祖先节点有3和5，7的是3，5，2。所以6和7的公共祖先是5。如果用代码实现，需要考虑好几种情况。根据

以上定义，若root是p和q的最近公共祖先，则只可能为以下情况之一：

1. p和q在root的子树中，且分列root的异侧（即分别在左右子树中）
2. p = root，且q在root的左或右子树中
3. q = root，且p在root的左或右子树中

而具体在执行递归时，我们要判断的情况稍微复杂一些：比如我们要在上面的树中查找6和7的公共祖先，遍历的时候从树的根节点开始逐步向下，假如某个时刻访问到了节点为root，我们通过后序递归的查找其左右子树，此时的判断逻辑是：

• 如果left和right都是null，说明在该子树root里面p和q一个都没有，直接返回null即可。例如上图中递归到的root为1的子树时；
• 如果left和right都不为空，说明p和q分别在root的两侧，例如root为5，此时6和7就分别在其两侧，直接返回5就好
• 当right 为空，left不为空，此时情况比较复杂，还要考虑两种情况
  • 首先：判断一下root 是不是p或者q，如果是说明p和q一个是另一个的祖先，直接返回就好
  • 其次：说明right子树里面什么都没有查到，而6和7在left子树里，此时需要递归去左子树查询即可，例如root=3时，此时需要递归的结果必然时right为空没不是left不为空。
• 如果left为空，而right不为空，说明和上面一条相反。

分析了这么多，那么代码要怎么写：

    /**
     * 寻找最近的公共祖先
     * @param root
     * @param p
     * @param q
     * @return
     */
    public static TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {
            return root;
        }
        // 左右
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        // 有点类似剪枝
        if (left == null){
            return right;
        }
        if (right == null){
            return left;
        }
        return root;
    }	

---

总结

提示：祖先问题