【数据结构】顺序查找，折半查找，分块查找的知识点总结及相应的代码实现

news2024/10/3 3:25:49

1、顺序查找

定义及步骤

代码实现

2、折半查找

定义及步骤

代码实现

折半查找判定树

3、分块查找

定义及步骤

1、顺序查找

定义及步骤

顺序查找的定义：从数据集合的起始位置开始，逐一比较每个数据元素，直到找到所要查找的元素或者遍历完整个数据集合为止。适用于顺序表，链表，表中元素有无顺序都可以。其时间复杂度为O(n)，其中n为待查找元素个数。

具体步骤如下：

从集合的第一个元素开始顺序遍历，直到找到目标元素或者遍历完整个集合。
若遍历到的元素与目标元素相同，则返回该元素的位置。
若遍历完整个集合仍未找到目标元素，则返回未找到的标识（通常为-1）。

代码实现

下面是 C 语言实现顺序查找（带哨兵）的示例代码：

#include <stdio.h>

#define MAXSIZE 100 // 定义最大容量

typedef struct {
    int data[MAXSIZE+1]; // 数据存储数组，从 data[1] 开始存储数据
    int len; // 当前长度
} SeqList;

// 初始化顺序表
void initList(SeqList *list) {
    for (int i = 1; i <= MAXSIZE; i++) {
        list->data[i] = 0;
    }
    list->len = 0;
}

// 插入元素
int insertList(SeqList *list, int elem) {
    if (list->len >= MAXSIZE) { // 判断是否已满
        return 0;
    }
    list->data[++list->len] = elem;
    return 1;
}

// 带哨兵的顺序查找
int searchList(SeqList *list, int elem) {
    int i;
    list->data[0] = elem; // 设置哨兵
    for (i = list->len; list->data[i] != elem; i--); // 从后向前遍历查找
    return i; // 返回查找到的位置
}

int main() {
    SeqList list;
    initList(&list);
    insertList(&list, 1);
    insertList(&list, 3);
    insertList(&list, 5);
    insertList(&list, 7);
    insertList(&list, 9);
    int pos = searchList(&list, 5);
    if (pos == 0) {
        printf("未找到\n");
    } else {
        printf("找到了，位置为：%d\n", pos);
    }
    return 0;
}

在上面的代码中，我们定义了一个 SeqList 结构体来实现顺序表，其中包含了数据存储数组和当前长度。使用 initList 函数进行初始化，使用 insertList 函数插入数据。在 searchList 函数中，我们设置了一个哨兵，然后从后向前遍历查找，如果找到则返回位置，否则返回 0 表示未找到。在主函数中，我们创建了一个顺序表，插入了一些数据，然后进行查找，输出查找结果。

2、折半查找

定义及步骤

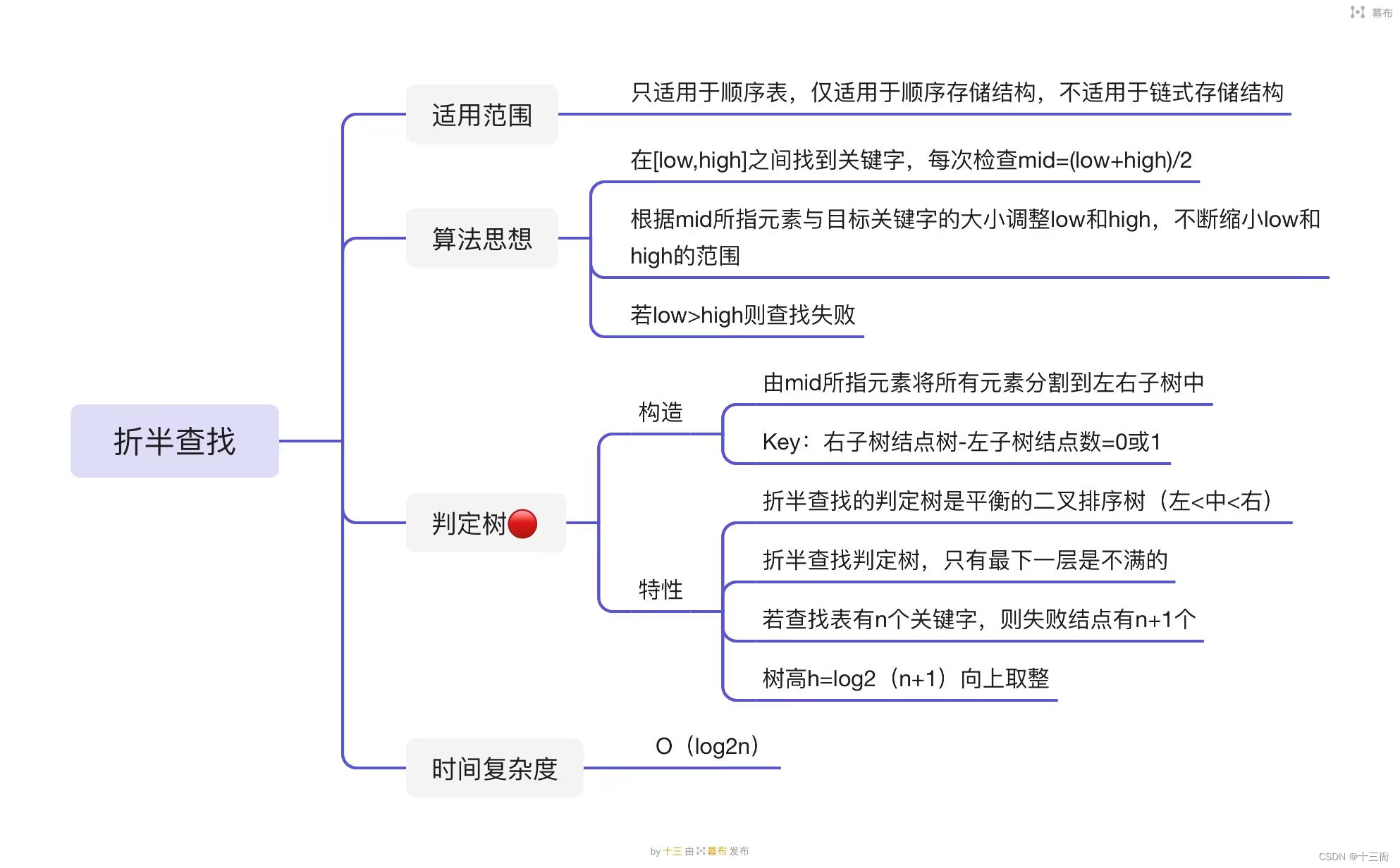
折半查找（Binary Search）又称为二分查找，是一种基于比较目标值和数组中间元素的查找算法。该算法的前提条件是数组必须已经有序。只适用于顺序表，仅适用于顺序存储结构，不适用于链式存储结构。

具体实现过程为：

1. 定义左右指针，分别指向数组的第一个元素和最后一个元素。

2. 然后取中间元素的下标，将目标值与此元素进行比较。如果目标值等于数组中间元素的值，则直接返回中间元素的下标。

3. 如果目标值小于数组中间元素的值，则将右指针移动到中间元素的左边一位。

4. 如果目标值大于数组中间元素的值，则将左指针移动到中间元素的右边一位。

5. 重复步骤2~4，直到目标值与中间元素相等或者左右指针相遇。

6. 如果左右指针相遇时，仍没有找到目标值，则表示该数组中没有目标值。

折半查找算法的时间复杂度是O(logN)，相对于顺序查找的时间复杂度O(N)而言，折半查找具有更高的效率。

代码实现

下面是 C 语言实现折半查找的示例代码：

#include <stdio.h>

int binarySearch(int array[], int left, int right, int x) {
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (array[mid] == x) {
            return mid;
        }
        else if (array[mid] < x) {
            left = mid + 1;
        }
        else {
            right = mid - 1;
        }
    }
    return -1; //表示未找到
}

int main() {
    int array[] = {1, 3, 5, 7, 9, 11};
    int x = 5;
    int n = sizeof(array) / sizeof(array[0]);
    int result = binarySearch(array, 0, n - 1, x);
    if (result == -1) {
        printf("未找到该元素\n");
    }
    else {
        printf("元素在数组中的索引是：%d\n", result);
    }
    return 0;
}

上述代码中，binarySearch函数的参数依次是数组array、数组左边界left、数组右边界right和要查找的元素x。函数通过while循环不断缩小查找范围，最终返回要查找元素在数组中的索引。在主函数中，我们定义了一个有序数组，然后调用binarySearch函数查找元素5在数组中的位置。如果返回-1，则表示未找到该元素；否则，返回元素在数组中的索引。

注意：该算法要求在查找之前需要先对数组进行排序。因此，如果数组没有排序，需要先调用排序算法进行排序，再进行查找。

折半查找判定树

折半查找判定树（Binary Search Decision Tree，BSDT）是一种二叉树，用于解决折半查找（Binary Search）问题。在BSDT中，每个节点代表一个比较操作，左节点表示小于比较值，右节点表示大于比较值。叶节点代表查找成功的结果，非叶节点代表查找失败的结果。

例如，对于一个长度为7的有序数组[1, 2, 3, 4, 5, 6, 7]，对应的BSDT如下图所示：

                ______4______
               /            \
          ___2___          __6__
         /       \        /     \
        1         3      5       7

在BSDT中，从根节点（4）开始，如果要查找数字3，则先和根节点比较，由于3小于4，因此向左子节点（2）移动。然后再和2节点比较，由于3大于2，因此向右子节点（3）移动。最终到达叶节点，查找成功。

对于长度为n的有序数组，BSDT的高度为log₂(n)，因为每次比较可以剔除一半的数据，因此最多需要比较log₂(n)次。由于BSDT的高度与数据的顺序无关，因此对于任何有序数组，BSDT都可以处理。

虽然BSDT的时间复杂度是O(log₂(n))，与折半查找一样，但是BSDT比折半查找更适合用于动态数据集合，因为BSDT可以实时更新，支持插入、删除等操作。