目录
前言
国内外研究现状
三维激光扫描对桥梁损伤检测的研究现状
基于点云高斯曲率损伤检测的研究现状
柱体偏差检测技术研究现状
存在的问题
法向量约束高斯曲率的 TLS 桥面潜在损伤区域探测
2.1 高斯曲率探伤的基本理论
2.2 点云拓扑关系建立的方法比较
2.2.1 KD-Tree 算法
2.2.2 三维栅格算法
2.3 桥面局部点云的曲面拟合
2.4 基于法向量约束的高斯曲率估算
2.5 法向量约束高斯曲率的坐标转换法抗噪性能比较
切片法和水平截面法的墩柱倾斜研究
3.1 倾斜度偏差法基本思路
3.2 基于切片法的点云数据处理
3.2.1 桥墩切片点云平面拟合
本文篇幅较长,分为上下两篇,下篇详见单期点云的高斯曲率定位桥梁潜在损伤技术研究(续)
前言
随着交通路网的布设以及城市现代化的飞速发展,大批桥梁应运而生,而伴随出现
的桥梁损伤问题也越来越引起重视。在交通量大且运营压力大的今天,由于桥梁长期超
载运营,加上复杂的地质情况、雨水冲刷侵蚀、桥面上车辆的重量超载以及一些人为的
基础差异
[1]
,使得桥梁结构疲劳损伤日趋严重,结果将会导致桥梁的老化、病害,甚至
是在使用过程中突然坍塌。如
2019
年
10
月
12
日江苏无锡发生高架桥侧翻,酿成
3
人
死亡
2
人重伤;
2020
年
3
月
2
日,福州发生桥梁的梁体突然轰然倒塌事故,造成
2
人死
亡
4
人受伤;
2021
年
12
月
18
日,湖北省鄂州市境内的沪渝高速桥向转大广高速的一段
500
米长的匝道桥发生侧翻,导致
3
辆货车坠落、
1
辆小轿车被压等。桥梁变形是一种
客观存在的普遍现象,任何桥梁在投入使用后都会产生变形。若变形不太显著且符合规
定
,
说明桥梁是健康的。但若变形超过了一个限定量
,
就很有可能导致危害发生。然而
大多数桥梁变形初期墩柱和桥面不会产生明显特征,而这正是桥梁损坏的初始阶段
[2]
,
也是桥梁的潜在损伤。因此,及时监测桥梁,发现并评估桥梁结构的潜在损伤位置和损
伤程度,预测桥梁结构性能的变化对保障人民生命财产安全具有重要的意义。如何探测
桥梁的潜在损伤情况,预防事故的发生,已经成为当前社会的一个热点问题。
目前,桥梁损伤检测的主流方法是通过非接触式传感器,如全球定位系统(
Global
Positioning System
,
GPS
)、全站仪、星载干涉合成孔径雷达(
Interferometry Synthetic
Aperture Radar
,
InSAR
)、地基合成孔径雷达(
Ground Based Synthetic Aperture Radar
,
GB-SAR
)等技术对桥梁进行连续,定期定点观察,从而对桥梁的施工安全和性能做出
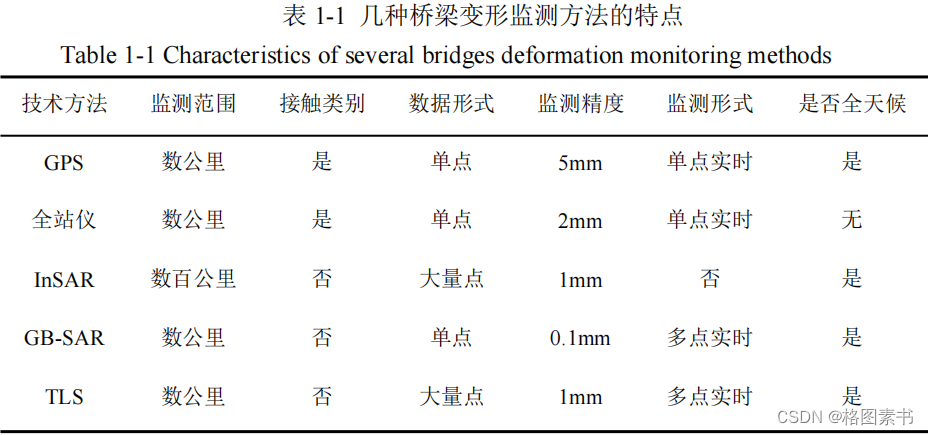
评估。虽然这些检测方法在点位和角度的检查中精准程度较高,如表
1-1
所示,但受限
于测量范围小,耗时费力的特点,其结果很难精准定位到桥梁关键损伤位置。且因为桥
梁结构的特殊性,绝大多数的损伤和潜在损伤发生在桥面的侧面或者底部,专业检测人
员需要借助一定的机械设备才能精准探测这些位置。

地面三维激光扫描技术具有采集数据点多、数据量大、非接触性等优势
[3]
。其可以
计算出被测物体与扫描仪的空间距离
[4-7]
。在桥梁损伤检测中,测量结果通常包括采集点
的几何信息和特征信息。通过保存点云三维空间结构,实现全面、可视化、精准测量的
结果。然而,三维激光扫描测量具有随机性和多次扫描不可重复性,采集的周期性数据
会直接影响桥梁健康评估的时效性,降低损伤评估效率。基于此,本文采用单期点云高
斯曲率的损伤检测方法,其核心思想是基于统计学的原理,通过从测量数据中提取特征
参数,将每个点的曲率变化作为损伤程度的指标进行分析。相比于采集多期点云对比,
找出差异区分析,这种方法更加灵活,不需要大量计算。因此可以将其视为一种测量辅
助方式,先找到桥梁的潜在损伤区域,再结合其他手段精准探伤,保证数据时效性的同
时,提高检测效率。
国内外研究现状
三维激光扫描对桥梁损伤检测的研究现状
最早的三维激光扫描技术进行应用于
20
世纪
60
年代。由于当时仪器精度的局限,
很少有人将此技术应用在变形监测领域,随着科技的持续发展,使得仪器的自动化和精
准度越来越高,三维激光扫描技术在变形监测领域逐渐应用起来
[8]
。此后,人们也开始
逐步将该技术应用于桥梁的变形监测和损伤检测。在过去十年间,从
2010
年开始,国
外学者
Armesto
等
[9]
就对古建筑拱桥的变形进行监测,在设有参数对桥梁整体信息采集
前提下,使用三维激光扫描技术对点云数据采用建模方法分析,获取桥拱的几何尺寸,
分析拱表面的脱落和损伤。
Riverio
等
[10]
也用地面三维激光扫描仪对石拱桥进行了扫描,
利用获得的点云数据和监测算法生成了石拱桥的三维模型,并对桥面及侧面的结构进行
受力分析。此后在
2016
年,
Delaloye
等
[11]
通过两期桥梁整体的点云数据,使用椭圆拟
合算法获得桥梁的相对变形,并根据周围环境分析变形的原因。在
2018
年,
Matsumoto
等
[12]
利用地面三维激光扫描仪对缅甸的
Twantay
大桥进行了扫描,将三维激光变形监测
法和有限元分析法对古建筑拱桥的变形进行监测,对比多期数据找到变形区域。
2019
年,
Pfeiffer
等
[13]
通过提取大桥的特征点线,计算桥梁的挠度变化,并与
GPS
特征点的
监测值相比,监测结果可靠。同年,
Rashidi
等
[14]
在点云逆向建模中借助可视化编程软
件,按照结构单元点创建桥梁真实结构模型,生成完整参数化桥梁信息模型,分析形变。
国内在变形监测方面的研究相较于国外较晚,
2011
年,国内学者苏磊
[15]
总结了三维
激光扫描对桥梁变形分析方法。
2012
年,熊友谊
[16]
使用三维激光扫描仪对佛山三山南
桥进行了荷载测量,通过加载不同的荷载量,证明了将该技术应用于桥梁变形分析可靠。
此后在
2017
年,徐进军
[17]
等人提出了点云拟合建模方法和重心查找方法来进行变形计
算,分别使用这两种方法获取桥面荷载不同的挠度变化。同年,吉林大学的卢颖
[18]
对旧
桥采集了点云数据,结合桥梁的尺寸大小和荷载变化,有效建立有限元模型,更准确的
完成了桥梁形变检测。之后在
2020
年崔海文
[19]
对大桥进行三维激光扫描,发现由 Midas
有限元计算获取的位移测点值与三维激光扫描所获取的位移测点值基本一致,存在的偏
差在
0.5mm
以内,证明了该技术的实用性。
2021
年,熊文和李刚等
[20]
学者,采用桥梁
形态及结构受力法,利用骨架法对桥梁构件进行单体分割,对配准相对不动点集进行优
化,结合多期点云数据分析不同时段内构件的形态变化。
基于点云高斯曲率损伤检测的研究现状
Teza
[21]
等在其损伤区域研究中,使用高斯曲率来识别受损区域的数据集。如果该子
区域高斯曲率的标准差大于参考区域高斯曲率的标准差,则将子区域视为损坏。
Liu
[22]
等人提出了以行网格和列网格中数据点的距离和高斯曲率作为检测混凝土桥梁延伸桩
承台缺陷区域的标准。
Mizoguchi
[23]
等利用最小二乘法将基于点云的原始表面拟合到未
受损区域。然后根据缩放区域的点云到地面的距离计算总缩放深度,比较高斯曲率的变
化,判定损伤。
Medioni
[24]
提出一种基于空间点云几何信息识别的方法,该方法通过归
类的方式将散点的曲率信息在点云中划分,每个散点的曲率值都是从邻域点参考的结果,
该方法能辨别稳定的建筑物信息,然而其对噪声点不敏感,不易有效区分,且计算复杂
度高。
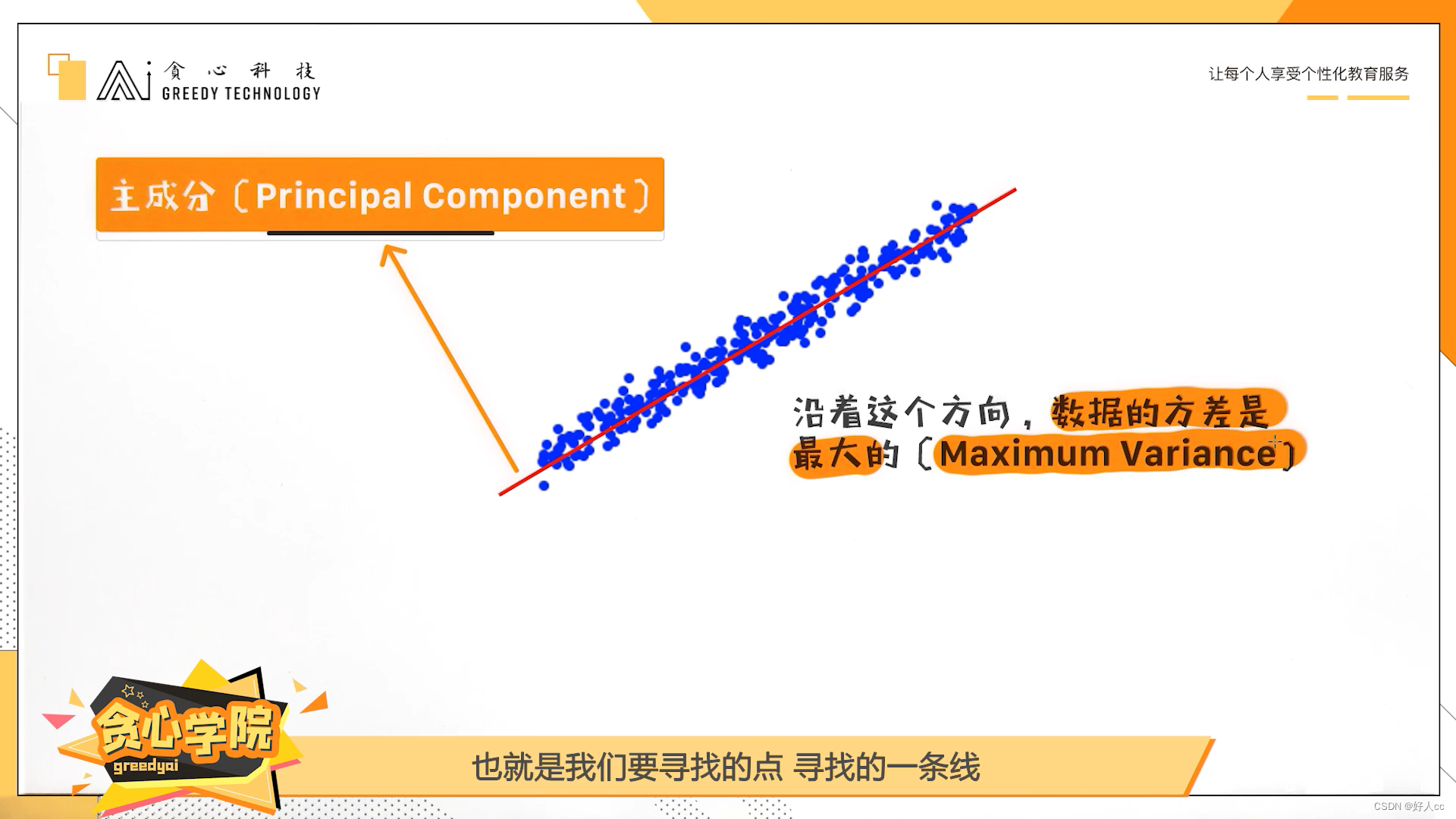
Pauly
[25]
一个根据主成分分析法对临近点进行多尺度提取信息的方案,该办法的
核心内容是根据测量相应点的协方差矩阵的特征值,来确定局部点云的高斯曲率,缺点
是计算量比较大。
Demarsin
[26]
提出了一个可以从目标点云获得和建立封闭的尖锐曲率特
征提取算法,这种方法先通过主成分分析算法获取各个节点的法向量,接着再通过对法
向量的变换在点云的邻域内实现点云分割,然后再建立最小生成树并获得检测的特征面
的曲率特征。
在桥梁损伤检测方面,基于点云的高斯曲率也有相关研究,吴杰等
[27]
学者通过三维
点云数据对实验室玻璃桥主梁的不同开裂程度、不同裂缝条数以及不同开裂位置的曲率
曲线进行了损伤程度的识别。
Chu
等
[28]
学者通过开裂箱梁模型表面的离散点云数据,发
现由弯矩引起变形的地方曲率存在突变,发现曲率对结构损伤十分敏感,能够反映箱梁
开裂的地方。吴桐和周志祥等人
[29]
,采用多期点云数据对比,将采集的实验室模型桥数
据比较,计算挠度差值的高斯曲率,结果证明当桥梁结构出现损伤后,可以利用高斯曲
率的变化进行定位。夏文传
[30]
提出两个空间曲面相关性概念和灰色高斯曲率关联系数
,
并将其应用到基于桥梁静载试验的损伤定位中。
柱体偏差检测技术研究现状
桥梁柱体作为整座大桥的脊梁,将上部结构全部荷载传递到基础上,其质量的好坏
直接影响着桥梁的整体服役寿命
[31]
。桥墩垂直度偏差问题历来都是中外学者的论文研究
重点
[32-35]
。铁怀民等
[36]
利用有限元模型对桥墩垂直度偏差问题进行了量化分析,结果
表明桥墩垂直度偏差对桥墩的抗裂性能和承载能力影响较大。丁克良等
[37]采用全站仪自
由设站无接触测量方法,实现了桥墩垂直度的快速测量。邱冬炜等
[38]
通过改进最小二乘
拟合圆曲线的方法,快速检测分析桥墩垂直度。上述研究的主要依据是全站仪测量得到
的少数数据值,但是桥墩作为一个三维立体结构,在使用过程中,最大偏差值出现的位
置并不可预测。仅依靠全站仪测量的有限个特征点来确定桥墩垂直度的方法存在很大局
限,测量结果的实用性不强。
针对全站仪的不足,很多学者将三维激光扫描技术引入到柱体检测中,
Jacky
等
[39]
针对三维激光扫描的不规则点云数据,提出了适用于空间内建筑物最小二乘质心提取方
法,通过采集完整的柱体点云数据,构件三维模型,寻找到柱体的质心,完成对柱体的
倾斜判断。
Nguyen
等
[40]
设计了点云处理和垂直度指标的快速提取算法,用于管道柱体
的长度和半径大小和尺寸检查。
Madrigal
等
[41]
提出了一种检测三维点云中平面平整度的
检查方法,主要利用点云中点的分布直方图(
MPFH
),用于检测柱体表面的缺陷以及
倾斜度。欧斌
[42]
分别选取将所测的桥墩数据,将桥墩数据分为多段柱体,计算每段点的
倾斜度,最后整体拟合,进行检测。徐翰
[43]
等提出了空间网格划分位置的方法,将柱体
顶端和底端纳入到不同网格,根据点云差异给点云赋予不同色谱颜色,可直观的看出柱
体点云的倾斜差异。李斌
[44]
将徕卡
Nova MS50
全站扫描仪应用在电厂烟囱变形监测中,
通过两期烟囱点云图,结合色谱分析,判断倾斜幅度。
存在的问题
(
1
)对于桥面,基于点云高斯曲率的损伤探测多数是从结构局部刚度损伤与挠曲
线曲率的关系出发,结合有限元的方法对模型桥分析,主要判别桥梁中是否存在裂缝。
而实际桥面的损伤类型还包括挠度变化,表面混凝土破损和脱落等,以上方法并不适用
区分和评估损伤。同时,实际采集的桥面点云数据,数据量大,杂乱无章且伴随着噪声。
如何快速准确的计算出海量点云数据的高斯曲率和选择合适的高斯曲率算法去除噪声
干扰,需要更深一步的理论研究和实验验证。
(2
)对于桥墩,基于点云垂直偏差检测的研究较少,没有形成系统全面的方法,
垂线法和全站仪测量法依旧是当前检测方法的主流。且多数学者在研究桥梁损伤时,是
将桥面和桥墩分开研究。但因为桥墩既要承受桥面的竖向荷载,也要承受水平荷载和斜
向荷载等,因而可能会产生较大的侧向变形,直接对桥面的稳定性造成影响。所以,研
究桥墩的损伤机理,结合桥墩对全桥的安全性能分析至关重要。
法向量约束高斯曲率的 TLS 桥面潜在损伤区域探测
2.1 高斯曲率探伤的基本理论
动挠度是桥梁安全状态评估的重要指标之一
[45-49]
,表示结构在荷载作用下产生的竖
向变形。由于桥梁结构形状相对复杂,且每日承载着巨大车流量和人流量,所以桥面通
常设计为曲面,这样做的目的是最大程度规避动挠度因素的影响。在微积几何学中,曲
面是一条条动线,是对空间里连续运动的轨迹的表现,而曲率是对曲面弯曲程度的刻画。
高斯曲率被定义为二次可微曲面的显著微分量,是曲面的一个固有量。如果曲面受到规
律的弯曲或其他等距变换的影响(即连续的可逆变换与它们的逆变换一起可微),高斯曲
率是不变的
[50]
,而当桥梁受到损伤后,其内部高斯曲率则会变化异常。利用以上特性,
本文中在对桥梁曲面形变检测时,基于高斯曲率数值的突变,通过可视化的方式将桥梁
曲面的损伤位置和程度表现出来。但在实际采集的点云数据中,往往有更多的噪声干扰,
影响数据的精准度。所以选择合适的高斯曲率估算方法,最大程度的抑制噪声,是本章
研究的重点,技术路线图如下:






2.2 点云拓扑关系建立的方法比较
点云拓扑关系是指点、线和面等几何要素描述物体间的相邻、相切、相离和包含关
系。生成拓扑的好处是:(
1
)利用拓扑关系,不用求取坐标和距离,就可以确定同一
空间内两个三维物体的位置关系。(
2
)通过拓扑关系可以查找到同一数据集的要素;
(3
)按照拓扑关系生成几何体,如根据曲率生成圆、点与点之间的连线生成几何体等。
拓扑关系可以体现物体之间的位置结构关系,不会因为观察维度不同而产生变化。一个
拓扑关系存储了三个参数:规则、等级和拓扑容限。规则明确了拓扑的空间形态,决定
了各要素的相互关系,只有在一个以上的拓扑规则下,才能生成拓扑。等级规定了由低
等级要素向高等级要素移动。生成拓扑关系时,必须对要素分级。拓扑容限反映了在一
定空间大小内,节点和几何边被搜索到的最小量,拓扑容限的大小取决于数据,初始的
拓扑容限值由系统依据数据之间的关系计算出来。利用雷达、激光扫描仪、立体照相机
等三维检测装置所得到的点云数据信息,往往具有信息量大、分布不均衡等特征。点和
点间缺乏拓扑关联,即为不规则点云。而点云数据处理中,如滤波、分割、以及曲率运
算等,一般都是建立邻域,对周围的点云进行分类归纳,以达到快速查找临近点的效果,
也是建立点云拓扑关系的重要价值。通常,构建邻域的方法有两种:①
KD-Tree
算法,
②三维栅格法。
2.2.1 KD-Tree 算法
KD
树(
K-Dimensional
树的简称),是一种分割
K
维数据空间的数据结构,主要
应用于多维空间关键数据的最近邻查找(
Nearest Neighbor
)和近似最近邻查找
(Approximate Nearest Neighbor)
。理论上,
KD-Tree
就是邻域搜索树(
Binary Search Tree
,
BST
)的另外一种表现形式。邻域搜索树的基本特性如下:①每当树的左分枝有值,则
左分枝中每个结点的值都系相当于其根结点的指数。②同理,如果它的右分枝都不为空,
那么右分枝每个结点的值都相当于其的根结点的值;③它的两个分枝就是各自的搜索树。
如下图 2-3 所示:


如果我们处理的对象集合是一个
K
维空间中的数据集时,首先要明白的问题是:怎
样将一个
K
维数据划分到左枝树或右枝树。在构造一维邻域搜索树时,当前节点的选择
并非经过对
K
维数据进行总体的比较,而是选择某一个维度
d
,而后比较两个
K
维数据
在相同维度
d
上的大小关系,即每次选择一个维度
d
来对
K
维数据进行划分,相当于
用一个垂直于该维度
d
的平面将
K
维数据空间一分为二,平面一边的全部
K
维数据在
d
维度上的值小于平面另外一边的全部
K
维数据对应维度上的值。当我们实际采集了一个
三维空间的点集时,需要我们将数据集进行切割和划分,保证每个区间只有对应的数据。
具体流程:如果对某一个三维空间按照上述方法划分,就会把
K
维度的主空间分割为多
个子空间。以此类推,如果我们继续按照同样方法划分子空间,还会获得新的空间,一
直重复这个流程直到确保每个子空间不需要分割为止。这个过程需要考虑两个方面:
(
1
)选择维度:通过统计样本在各个角度上的方差变化,然后选择相对方差变化
较大的那些角度。数据方差大,表示沿该位置轴上统计结果点相对较为分散。在这种方
位上,进行统计分配才能达到最佳的平衡点。
(2
)平衡
KD-
树:在某一维度
X
上进行划分时,划分点(
pivot
)必须获得维度
X
上所有数据的算数均值,这样计算出的多个子集合数据量就基本相同了,可以平衡
KD-
树生长。
当对
KD-
树生成时:从
K
维度数据集中选取有较大差异的维度
K
,然后用从该维度
上选取中值
m
的
pivot
对该数据集进行分割,以此获得了两个子集合;同时建立了一个
子树结点
node
,以进行保存;通过对两个子集合重复(1
)步骤的程序,直到每个子集
合都没有再划分出来
;
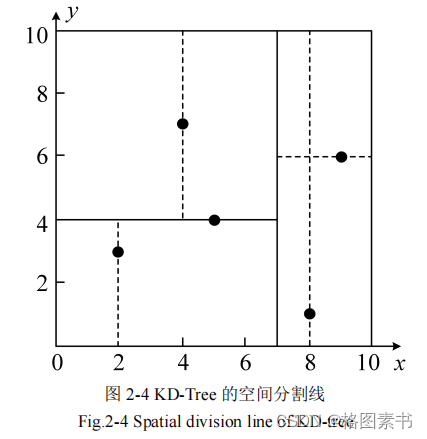
假设有
6
个二维数据点
{
(2,3
),(
5,4
),(
9,6
),(
4,7
),(8,1
),(
7,2
)
}
,
数据点位于二维空间内(如下图中黑点所示)。
KD-
树的目的就是要研究空间中的分割
线。下面的步骤就要讨论
KD-
树界定分割线的过程:
1
)分别计算横,纵坐标方向上数据的均方差,得知横方向上的均方差最大;
2
)根据横轴方向的值
2,5,9,4,8,7
按照从小到大排序得到中间值为
7
,所以该
node
中的
data=
(7,2
)。这样,该节点分割的面就包含点(
7,2
),且直线
x = 7
的直线垂直
该面;
3
)确定左子空间和右子空间。分割平面
x = 7
将整个空间分为两部分,
x < = 7
的部
分为左子空间,包含
3
个节点
{
(2,3
),(
5,4
),(
4,7
)
}
;另一部分为右子空间,包
含
2
个节点
{
(9,6
),(
8,1
)
}
。如下图 2-4 所示:

将搜索统计结果
Q
从根节点出发,再通过
Q
与所有节点的对比结果向上下行造访
KD-Tree
,然后直接到达叶子结点。在这里
Q
与节点的对比结果指的是把
Q
相对于结点
中的
k
层次上的数值和中值
m
加以对比,如果结果
Q (k)<m
,则抵达左子树,否则抵达
右子树。到根叶的顶点时,通过统计
Q
和在叶子结点上存储的所有统计结果间的相距,
并记下最少相距对应的所有统计结果点,记为最近邻点
nearest
和最少相距
dis
。以实现
回溯功能。进入该节点,并完成与第一个步骤一样的搜索步骤,一旦发现相距较近的数
据节点,则调整为距离当前的最近邻点
nearest
,并调整为
dis
。如果统计结果
Q
与上一
结点没有被搜索的树支距离不超过
dis
,可以确定该树支上存在离
P
更近的数据,通过
定位该结点,按照和之前一样的搜索步骤,当找到更近的数据点时,则更新为当前的最
近邻点
nearest
,并更新
dis
。如果统计结果
Q
与上一结点没有被搜索的树支距离超过
dis
,
可以确定没有邻近点。
2.2.2 三维栅格算法
栅格化法是将点云数据的外围包裹一个大的正方体,设置阈值参数的边长长度,对
每条线进行平均分割,从而产生多个小正方体的单元格,即为栅格。如下图 2-5 所示:
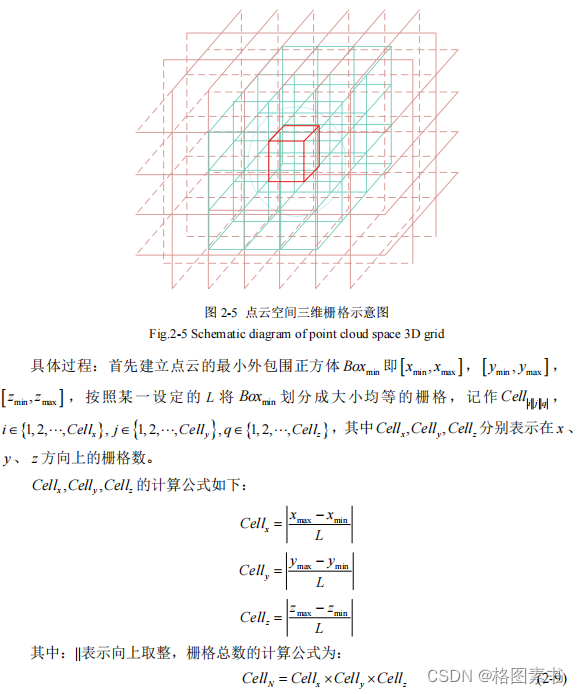


栅格全面化,给划分后的每一个小栅格编号,使每个栅格与每部分点相关联。当建
立拓扑关系后,对某一点
Pi
进行
K
近邻搜索时,就可以把搜索范围定位到
Pi
所在栅
格内以及其上下、左右、前后相邻的栅格内。如果
Pi
位于栅格的某一条线附近,那距
离
Pi
最短的点可能被纳入到其相邻栅格内,而我们要做的就是在其相邻栅格搜索。在
搜索过程中必须要满足数量
K
个,如果栅格的邻域都搜索完毕依然不足
K
个,那就以
每个邻域栅格为基准,依次搜索上下、左右、前后的栅格,直至满足条件,搜索结束。
上述提出的方法,是先通过栅格法,将海量的离散点云建立拓扑关系,并通过对各个栅
格内的点云拟合出一个球面方程,来得到该栅格内点云的曲率;通过设置给定曲率值,
来决定是否对栅格进行八叉树剖分,并在子栅格内进行拟合,以保证曲率变化大的区域
包含较多的细节信息。因为点云集的分布是不规律的,有些地方密集,有些地方稀疏,
所以在对点云处理前,要确保点与点之间相互关联,通过对离散点应用三维栅格法,来
进行离散点云拓扑关系的建立。在给定合适的栅格宽度,曲率后,对每个栅格内所有点
拟合出球面方程,根据拟合出的球面方程估算球面方程的曲率,并用估算出的球面方程
的曲率和给定曲率比较。来决定是延展到该栅格的
26
近邻还是进行八叉树剖分,并由
此来对曲率较大处的区域保留较多的点,从而对点云局部分析。
根据两种方法的对比,我们可以发现,三维栅格技术虽然工作原理上比较简洁易懂,
但是实际运用起来却不很方便,特别在处理数据量大且密度分布不平衡的时候处理效果
不好。小栅格中边界长短划定就是一大难题,因为边界如果较大,会容纳更多的点云数
据量,很有可能造成数据冗余,加大计算工作量。而边界选择过小则会生成更多数量的
栅格,会对最后的拼接产生一定的影响。因为桥梁点云本身的特点,采集的点云具有无
序性,且点云的密度并不是均匀变化的,所有本文优先选取
KD-Tree
对点云拓扑关系进
行建立。
2.3 桥面局部点云的曲面拟合
为更好地对数据量大且形状复杂的曲面局部分析,需要先进行点云拟合,目前主流
使用一种算法
—
移动最小二乘法。这种新的最小二乘算法为点云数据的处理提供了新的
思路。使用点云数据拟合曲面时,考虑到点云的数据量大、形状复杂的特点,如果使用
传统的最小二乘法拟合可能会得到病态的曲面方程,从而导致较大的误差。而使用移动
最小二乘法拟合点云不仅能够减少误差,提升局部的准确率,还能避免分块拟合和平滑
化的过程,该算法基于点云法向量来进行。法向量是几何体表面的属性,在点云重建算
法,点云分割算法、点云降噪算法以及特征描述算法
[51]
也要通过精准的法向量才能取得
较好的效果。对于那些具体的物体表面,直接推断表面处某一点的法向量方向较为简单,
只需找到该点所在的曲面即可。而我们研究某一曲面局部点时,其范围相比某一点范围
更大,这样就形成两种不同的解决方法:①从点云集的局部特征着手,根据查找邻域点
确定该点的法向量。②生成曲面三维模型,从三维模型中提取各个方向的曲面,然后从
曲面模型中计算表面法线。
本文基于上一节拓扑关系方法的比较,按照第一种思路,从散乱的点集中直接进行
曲面拟合,根据这种情况进行分析,获取一个采集的点云数据集,对这个点集中的每个


构造候选点
P
n
为原点的局部坐标系,是利用局部点云数据拟合曲面,这是计算高斯
曲率的前提。局部坐标系的
XYZ
轴为主要坐标轴,对该坐标轴的求解即为求解候选点
的坐标系方向。在
K
邻域内采用移动最小二乘法将平面拟合,移动最小二乘法的核心思
想是将获取的点云集生成一个平面,利用点到平面距离的数学公式,求得每个点垂直于
该平面的法线,使得点集中所有的点到该平面距离的平方和最小。利用拟合平面的法向
量作为候选点
Pn的法向量。


通过运算得到拟合平面矩阵的特征值和特征向量。最小特征值对应的特征向量是该
平面的最小二乘解[52]。


2.4 基于法向量约束的高斯曲率估算
利用移动最小二乘法得到桥梁下表面点云的法向量估算后,由于该方法是将
P
n
的邻
域拟合平面后再计算法向量,因此估算出的部分法向量指向损伤方向的另一侧,为了后
续的计算,需要对法向量的方向进行调整。出现这种现象的原因是因为点云集中有多个
曲面拟合面的间距非常小,
P
n
的
K
邻域中会含有歧义邻域点,对于邻域点的选取会出现
重复或者丢失,通常导致法向量的方向发生错误,如图 2-7:
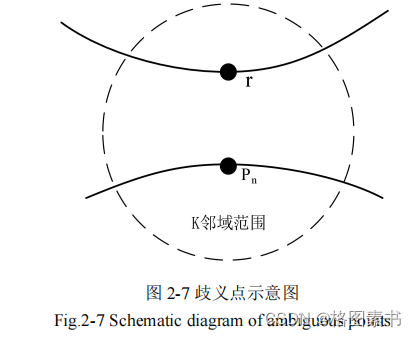

基于上述出现歧义点的情况,目前对于这种错误进行修改的主要方法分别为:邻域
增长法和法向距离法。邻域增长法的核心思想是通过增大相邻点的距离,避免出现一定
量的重合点来规避歧义点。法向距离法通过计算相邻两点的法向平均距离来衡量是否能


判定标准如表
2
-1:


由于法向距离法与邻域增长法都具有剔除歧义邻域点的效果,因此将两者组合会更
大程度上减少噪声干扰。组合时只需将邻域增长法的每个点都按法向平均距离
d
进行一
次歧义点剔除。当
d
i
=
0
时,法向距离法无法判断该点是否为歧义点,则改用邻域增长
法对该点进行判断是否为歧义邻域点。
将进行法向量调整后的桥梁下表面点云拟合平面的法向量作为坐标的竖轴,并以此
为基准分别进行旋转和平移,得到其所在的平面。此时即完成了候选点所在的临时坐标
系的建立。以法向量调整后建立的坐标系为基准坐标系,在此坐标系的基础上进行高斯
曲率的计算。高斯曲率是反映桥梁下表面点云状态的主要依据之一。根据微分几何的定
义[54]:其中第一基本量与第二基本量的转换关系分别为:


由于二次项系数恒大于零,因此该方程可以简化为一元二次方程。利用
Vieta
定理
进行求解,两根即为该曲面的两个主曲率,主曲率是该点在曲面的曲率的最大值与最小值[56],分别为:


高斯曲率实际上反映了桥梁下表面的曲率变化程度,如果桥梁未存在潜在损伤区域,
高斯曲率是不变的
[57]
。当高斯曲率快速突变时,意味着桥梁下表面发生了很大的变化,
同时说明存在潜在损伤区域
[58]
。
2.5 法向量约束高斯曲率的坐标转换法抗噪性能比较
由上文分析可知,当桥梁存在潜在损伤区域时,对应位置的高斯曲率会发生突变。
因此利用上述的处理方法,对北沙滩桥潜在损伤区域进行检测。但在点云数据采集过程
中,存在很多噪声,为了验证哪一种方法更适合本次采集的数据特点,截取北沙滩桥的
一处区域,进行抗噪性能比较。目前计算点云高斯曲率的方法主要分为五类,其中的交
叉曲面片法和坐标转换法的应用更为广泛,二者均可在实验环境下对平面上的点进行高
斯曲率的计算。但基于本文对桥梁的潜在损伤区域检测,在测量过程中,存在了不同程
度的噪声信号,为了能够适应本文的实验条件,因此选取交叉曲面片法与法向量约束高
斯曲率的坐标转换法在本文实验环境下对比。
对北沙滩桥进行三维建模,坐标系横纵轴均为表示桥梁曲面的位置信息,即由地面
三维激光扫描仪所获取的
XY
坐标,坐标系的
Z
坐标轴为高斯曲率的计算数值,通过
Z
坐标值大小,即可表示高斯曲率变化程度,结果如图
2-8
所示:

本次实验截取北沙滩桥某一损伤区域进行对比试验,通过进行对比可以发现:
(1)
图
2-8a
是交叉曲面片法(
Cross Patch
)对桥梁下表面点云特征进行提取结果图,
可以看出点云高斯曲率存在一定程度的干扰噪声,受到其邻域外的冗余点干扰较多,使
得该方法在实际计算过程中噪声占比较大,对高斯曲率的计算结果精度也有较大影响。
(2)
图
2-8b
则是本文采用的法向量约束高斯曲率的坐标转换法,其噪声数目较少,
降低了计算高斯曲率的歧义点,提高了计算高斯曲率模型的精确度。当进行邻域计算时,
不会因歧义点问题导致计算结果出现错误值,避免了在算法实现过程中桥梁下表面的点
云曲面存在较多点丢失的情况。
切片法和水平截面法的墩柱倾斜研究
3.1 倾斜度偏差法基本思路
倾斜度偏差表示线元素、面、中心平面、相切平面或者轴线相对基准在基本角度方
向上的变化程度。针对桥梁的损伤判别,除了要对桥面和桥墩沉降检测外,还应观察桥
梁墩柱的倾斜趋势变化,对桥梁整体做出合理的损伤评估。目前,多数桥墩倾斜检测采
用全站仪单点观测,需要根据柱体结构选取柱体表面多个关键点,通过测量关键点的坐
标进行计算对比,来确定桥墩的倾斜趋势变化,此过程存在耗费时间和人工财力等问题。
为了提高检测效率,本文提出一种使用三维激光扫描技术来对桥梁墩柱的倾斜监测的方
法,具体是使用三维激光扫描仪对桥梁墩柱进行扫描,将扫描的点云进行抽稀处理,提
取出点云的关键点以及连成的特征线,把数值拟合成光滑的曲线函数,通过对函数分析
计算出墩柱的倾斜角和斜率判断其倾斜趋势。
本节垂直偏差检测的原始数据是北京市北沙滩桥的墩柱点云,由于该桥附近车流量
大,地铁通行等,导致桥墩柱体有较大的倾斜幅度。实验步骤如下:首先计算桥墩点云
的平均密度,确定柱体切片的厚度和数量。其次,设置高程阈值将各桥墩的点云数据根
据高程阈值进行切片,再使用最小二乘拟合切片点云,提取拟合后的切片点云的圆心坐
标连接成线,该线即柱体点云的中心线。最后,将轴心线与空间坐标系
Z
轴进行偏差计
算得到两者之间的夹角值并对其进行分析。具体流程如图
3-1
所示:

3.2 基于切片法的点云数据处理
“切片”的概念最初来自于医用切割技术,将身体各种组织制作为切割并在光学显
微镜下观看,可以获得丰富多彩的生物医学图像。之后,逆向工程中引进了切片方法,
在缩减资料数量的时候,还可以把新的节点信息集拟合成轮廓曲线,并把这些轮廓信息
再加上先前求出的方向矢量信号进行重构曲面。基于切片方法的特点加载轮廓数据,整
个过程包括点云切割、点云稀释算法、分类算法、厚度去除算法和特征点检测算法,对
重点切块开展重点研究。本文沿用了上述方法的思路,基于桥墩点云数据包含各个位置
三维坐标信息的优势,通过对柱体点云的分割和提取,对每个墩柱进行分析,将桥墩顶
面,底面利用最小二乘法的方法进行边界拟合,同时求取各段高程的法向量方向,以便
计算出理论基准面,在此基础上筛选出与桥面平行的最佳基准面,按照这些基准面的方
向和角度把每个桥墩分为若干个切面,之后通过点集求取平均值的方法获得切片的中心
坐标,中轴线等关键数据。
3.2.1 桥墩切片点云平面拟合
由于本节研究的是桥梁墩柱,在近似圆柱的基础上,垂直于地面,因此所提取的切
片必须平行于地面,从平面中找到垂直于地面的平面也必定垂直于该切面。以往的学者
通过实验表明,总体的最小二乘方法在对散乱的点云数据平面拟合时具有较大的优势。
本文根据之前学者的理论研究,利用点到平面的最短距离原理和空间拆分法分析。在二
维空间中总体最小二乘的计算公式如下:




式
3-8
和
3-9
求得的两个参数表达式。由数学理论可知,式
3-6
具有
3
个随机变量,
使得我们无法获取最佳参数。因此该式不足以表达最佳基准面。我们需要本节中求得点
的法向量,根据法向量的表达形式来确定最佳基准面。垂直于桥墩的基准面虽然有很多,
但如何寻找到最佳基准面则是另一个需要解决的难题,因此我们首先需要明确“最佳”
的定义和应用范围。
根据式
3-13
、式
3-8
、式 3-9,即可确定最佳基准面公式如式:


不相同,因此我们要通过验证,找到最佳基准面。思想是通过点的方向去找面。但因为
采集的数据有较多的噪声点云,导致随机误差的存在,使得部分点的法向量并不与基准
面法向量平行。通常情况下,当法向量与准面法向量之间的夹角维持在一个较小的阈值
之间时,我们可以根据投影的位置偏位去排除噪声点。
接下来根据式 3-11 计算所有点的法向量与对应基准面法向量夹角余弦值之和的平


则由式
3-12
可知,理想基准面可以通过这种方式进行界定:基于每个点以及邻域
点的法向量,通过所有基准面
ave
cos
 j
的搜索,标记出变化量最小的
ave
cos
j
的搜索,标记出变化量最小的
ave
cos
 j
所对应的
j
所对应的
基准面法向量,该基准面法向量所垂直的基准面即为所求的理想切片面,通过已知变量,
获取该切片面的参数,找到最佳切片面。