目录

一、实验介绍

 二、实验环境

1. 配置虚拟环境

2. 库版本介绍

三、实验内容

0. 导入必要的工具包

1. 标量求导

2. 矩阵求导

3. 计算图

---

一、实验介绍

       PyTorch提供了自动求导机制，它是PyTorch的核心功能之一，用于计算梯度并进行反向传播。自动求导机制使得深度学习中的梯度计算变得更加简单和高效。

 二、实验环境

    本系列实验使用了PyTorch深度学习框架，相关操作如下：

1. 配置虚拟环境

conda create -n DL python=3.7 

conda activate DL

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

conda install matplotlib

 conda install scikit-learn

2. 库版本介绍

软件包	本实验版本	目前最新版
matplotlib	3.5.3	3.8.0
numpy	1.21.6	1.26.0
python	3.7.16
scikit-learn	0.22.1	1.3.0
torch	1.8.1+cu102	2.0.1
torchaudio	0.8.1	2.0.2
torchvision	0.9.1+cu102	0.15.2

三、实验内容

ChatGPT：

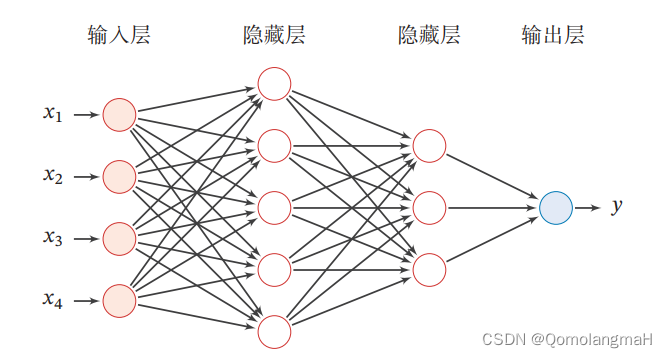
        前馈神经网络（Feedforward Neural Network）是一种常见的人工神经网络模型，也被称为多层感知器（Multilayer Perceptron，MLP）。它是一种基于前向传播的模型，主要用于解决分类和回归问题。

        前馈神经网络由多个层组成，包括输入层、隐藏层和输出层。它的名称"前馈"源于信号在网络中只能向前流动，即从输入层经过隐藏层最终到达输出层，没有反馈连接。

以下是前馈神经网络的一般工作原理：

1. 输入层：接收原始数据或特征向量作为网络的输入，每个输入被表示为网络的一个神经元。每个神经元将输入加权并通过激活函数进行转换，产生一个输出信号。

2. 隐藏层：前馈神经网络可以包含一个或多个隐藏层，每个隐藏层由多个神经元组成。隐藏层的神经元接收来自上一层的输入，并将加权和经过激活函数转换后的信号传递给下一层。

3. 输出层：最后一个隐藏层的输出被传递到输出层，输出层通常由一个或多个神经元组成。输出层的神经元根据要解决的问题类型（分类或回归）使用适当的激活函数（如Sigmoid、Softmax等）将最终结果输出。

4. 前向传播：信号从输入层通过隐藏层传递到输出层的过程称为前向传播。在前向传播过程中，每个神经元将前一层的输出乘以相应的权重，并将结果传递给下一层。这样的计算通过网络中的每一层逐层进行，直到产生最终的输出。

5. 损失函数和训练：前馈神经网络的训练过程通常涉及定义一个损失函数，用于衡量模型预测输出与真实标签之间的差异。常见的损失函数包括均方误差（Mean Squared Error）和交叉熵（Cross-Entropy）。通过使用反向传播算法（Backpropagation）和优化算法（如梯度下降），网络根据损失函数的梯度进行参数调整，以最小化损失函数的值。

        前馈神经网络的优点包括能够处理复杂的非线性关系，适用于各种问题类型，并且能够通过训练来自动学习特征表示。然而，它也存在一些挑战，如容易过拟合、对大规模数据和高维数据的处理较困难等。为了应对这些挑战，一些改进的网络结构和训练技术被提出，如卷积神经网络（Convolutional Neural Networks）和循环神经网络（Recurrent Neural Networks）等。

本系列为实验内容，对理论知识不进行详细阐释

（咳咳，其实是没时间整理，待有缘之时，回来填坑）

0. 导入必要的工具包

import torch

1. 标量求导

        对只有一个输出值的函数进行求导，结果是一个标量值。

# 最简单的情况，X是一个标量
x = torch.tensor(2, dtype=torch.float32, requires_grad=True)
y = x ** 2 + 4 * x
print(x.grad)
y.backward()
print(x.grad)

• 创建一个名为x的张量，其值为2，数据类型为float32，并设置requires_grad为True以启用自动求导功能。

• y = x ** 2 + 4 * x：定义一个新的张量y，其值为x的平方加上4乘以x。

• 在调用backward()函数之前，打印x的梯度值。由于还没有进行反向传播，x.grad的值为None。

• 通过调用backward()函数，计算y相对于所有需要梯度的张量的梯度。在这种情况下，只有x需要梯度，因此x.grad将被计算。

• 在调用backward()函数之后，打印x的梯度值，即导数。由于y是关于x的函数，并且我们通过backward()函数进行了反向传播，所以x.grad现在将包含y相对于x的导数值。

输出：

None
tensor(8.)

2. 矩阵求导

        对具有多个输出值的函数进行求导，结果是一个矩阵或向量。

x = torch.ones(2, 2, requires_grad=True)
print(x.grad)
# y是一个矩阵
y = x ** 2 + 4 * x
y.backward(torch.ones(2, 2))
print(x.grad)

• 创建一个2x2的张量x，其所有元素的值都为1，并设置requires_grad为True以启用自动求导功能。

• 在调用backward()函数之前，打印x的梯度值。由于还没有进行反向传播，x.grad的值为None。

• 定义一个新的张量y，其值为x的每个元素的平方加上4乘以x的每个元素。由于x的形状为2x2，因此y也将具有相同的形状。

• y.backward(torch.ones(2, 2))：通过调用backward()函数，计算y相对于所有需要梯度的张量的梯度。在这种情况下，只有x需要梯度，torch.ones(2, 2)表示将梯度初始化为2x2的全1矩阵。

• print(x.grad)：打印x的梯度值，即导数。由于y是关于x的函数，并且我们通过backward()函数进行了反向传播，所以x.grad将包含y相对于x的导数值

输出：

None
tensor([[6., 6.],
        [6., 6.]])

x = torch.ones(2, 2, requires_grad=True)
# y是一个矩阵
y = x ** 2 + 4 * x
y.backward(torch.ones(2, 2))
print(x.grad)

u = x ** 3 + 2 * x
# z是一个标量
z = u.sum()
z.backward()
print(x.grad)

• u = x ** 3 + 2 * x：定义一个新的张量u，其值为x的每个元素的立方加上2乘以x的每个元素。由于x的形状为2x2，因此u也将具有相同的形状。

• z = u.sum()：定义一个新的标量z，其值为u所有元素的总和。sum()函数将u中的所有元素相加得到一个标量值。

• z.backward()：通过调用backward()函数，计算z相对于所有需要梯度的张量的梯度。在这种情况下，只有x需要梯度，因为u是关于x的函数。

• print(x.grad)：打印x的梯度值，即导数。由于z是关于x的函数，并且我们通过backward()函数进行了反向传播，所以x.grad将包含z相对于x的导数值。

输出：

tensor([[6., 6.],
        [6., 6.]])
tensor([[11., 11.],
        [11., 11.]])

3. 计算图

        计算图是一种数据结构，用于表示数学运算的依赖关系。在深度学习中，计算图被广泛用于自动求导和反向传播算法。

        计算图由节点和边组成。节点表示操作或变量，边表示操作之间的依赖关系。在计算图中，变量通常被称为叶子节点或输入节点，操作则被称为内部节点或计算节点。

        计算图的构建过程包括以下步骤：

1. 定义输入节点（叶子节点）：将输入数据转换为张量，并设置其requires_grad属性为True，以便追踪梯度。
2. 定义计算节点：使用张量之间的数学运算（如加法、乘法、平方等）构建计算节点。
3. 构建计算图：将输入节点和计算节点连接起来，形成一个有向无环图，表示了操作之间的依赖关系。
4. 前向传播：通过计算图从输入节点到输出节点的路径，按照依赖关系依次执行数学运算，计算出输出节点的值。
5. 反向传播：从输出节点开始，沿着计算图的反向路径计算每个节点的梯度。根据链式法则，每个节点的梯度可以通过后续节点的梯度和该节点的局部梯度计算得到。
6. 梯度更新：使用计算得到的梯度值更新模型的参数，以进行优化和训练。

import torch

x = torch.tensor(2.0, requires_grad=True)
y = torch.tensor(3.0, requires_grad=True)
z = x**2 + y**3
z.backward()
print("Gradient of x:", x.grad)
print("Gradient of y:", y.grad)

输出：

Gradient of x: tensor(4.)
Gradient of y: tensor(27.)