糖果传递问题

问题描述

有 n 个小朋友坐成一圈，每人有 a[i] 个糖果。
每人只能给左右两人传递糖果。
每人每次传递一个糖果代价为 1。
求使所有人获得均等糖果的最小代价。

输入格式
第一行输入一个正整数 n，表示小朋友的个数。

接下来 n 行，每行一个整数 a[i]，表示第 i 个小朋友初始得到的糖果的颗数。

输出格式
输出一个整数，表示最小代价。

数据范围
1≤n≤1000000,
0≤a[i]≤2×109,
数据保证一定有解。

输入样例：
4
1
2
5
4
输出样例：
4

问题分析【公式推导过程】

话不多说，直接看图：我们令小朋友数组是a[N]，给出的是数组x[N]，这里的x可以是正数或者负数，正数代表给出，负数代表索取。
这里要求解的答案就是 |x1|+|x2|+|x3|+..... +|xn|的最小值

那么我们可以得到如下规律：

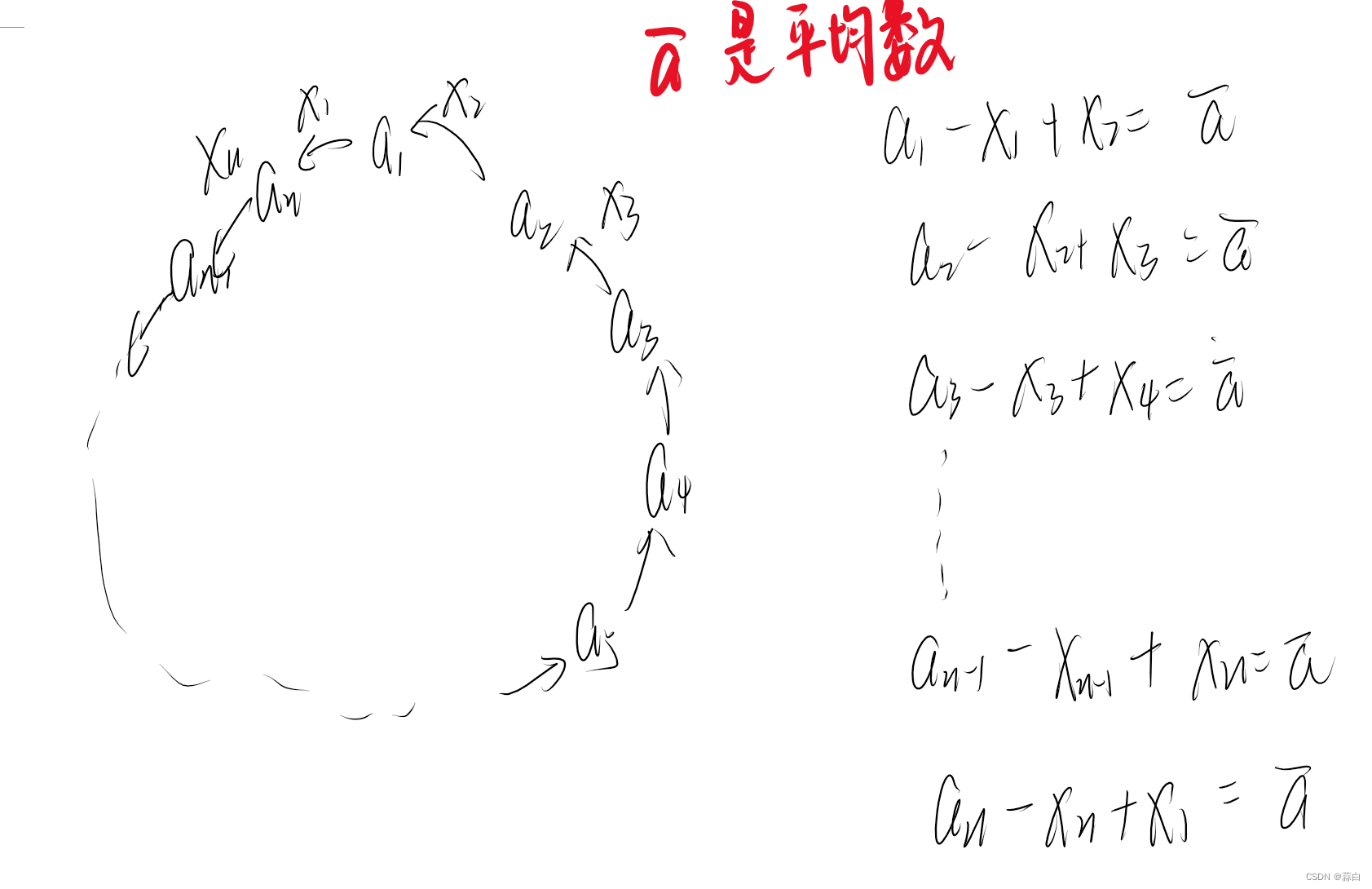
好了，我们现在尝试用x1来表示x2,x3,x4…，有如下的推导公式：

为啥会有个特殊式子产生呢？----因为这是一个环，我们要将这个环拉成一条直线。
寻找线型关系，所以对这个选项忽略掉。

我们将 1式 + 2式 有x3=x1-(a1+a2-2a);
同理，将 1式 + 2式 + 3式有x4=x1+(a1+a2+a3-3a);
按照这个规律地推下去，我们就可以用x1来表示x2,x3,x4…
得出的结论如下：

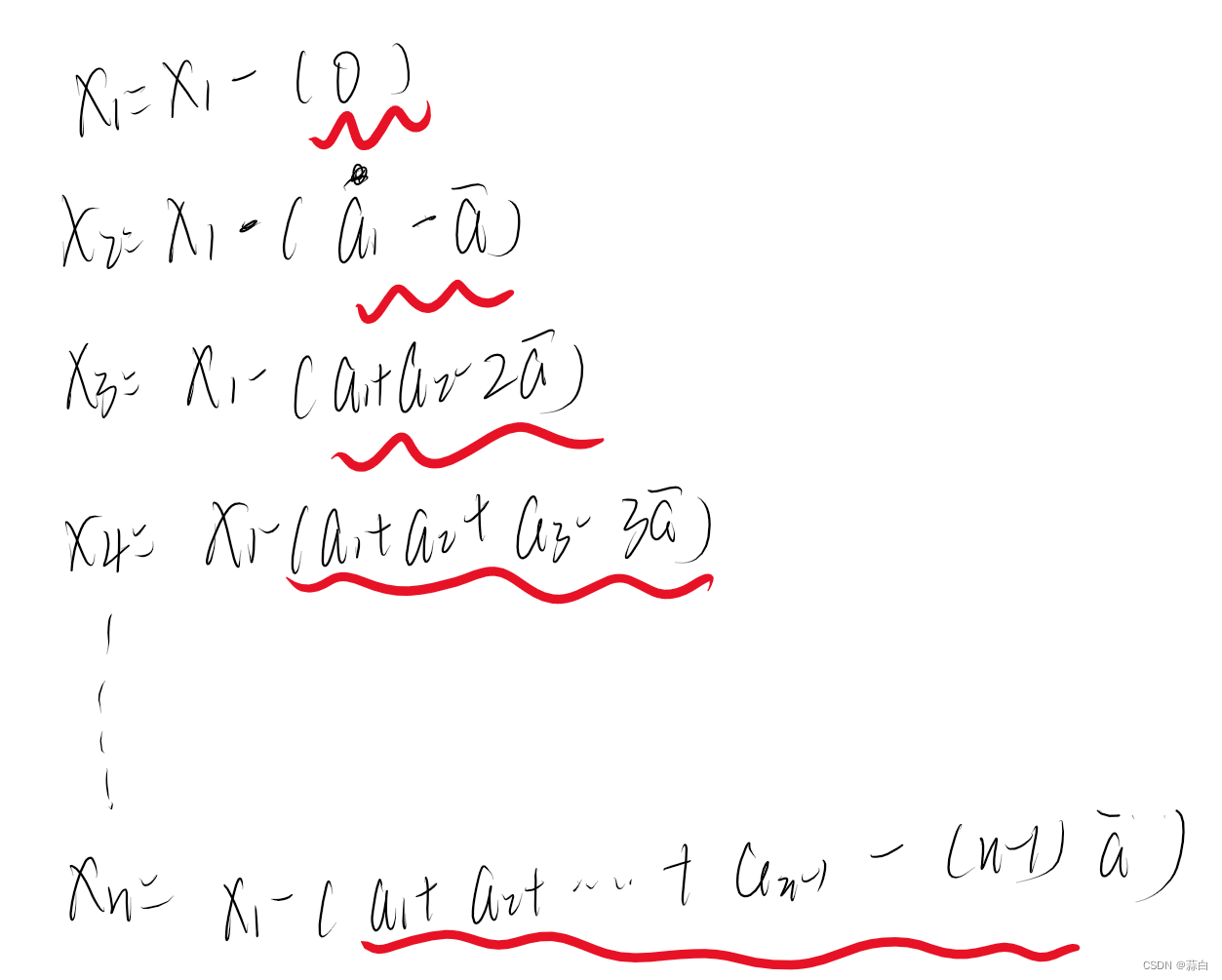
回到最初的结论：

这里要求解的答案就是 |x1|+|x2|+|x3|+..... +|xn|的最小值

我们可以将划红线的数值看成点，就是仓库选址的结论，若n 为奇数，那么最小选点就是中间点n>>1+1，若n是偶数，则是n>>1 ,n>>1+1都可以

这些点也有特征：

int ava=sum/n;
    for(int i=2;i<=n;i++){
        s[i]=s[i-1]+a[i-1]-ava;//ava是平均数
    }

代码

#include<algorithm>
#include<iostream>
using namespace std;
const int N =1e6 + 7;
int a[N],s[N],n;
typedef long long LL;
LL sum,res;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        sum+=a[i];
    }
    int ava=sum/n;
    for(int i=2;i<=n;i++){
        s[i]=s[i-1]+a[i-1]-ava;//ava是平均数
    }
    sort(s+1,s+n+1);
    int mid=s[(n>>1)+1];
    for(int i=1;i<=n;i++){
        res+=abs(mid-s[i]);
    }
    cout<<res<<endl;
    return 0;
}