1.散列表

1.散列表的定义

散列表(Hash Table)，又称哈希表。
是一种数据结构，特点是:数据元素的关键字与其存储地址直接相关。

特点：

• 若不同的关键字通过散列函数映射到同一个值，则称它们为“同义词”。
• 通过散列函数确定的位置已经存放了其他元素，则称这种情况为“冲突”。

2.处理冲突的方法1：拉链法(链地址法)

用拉链法（又称链接法、链地址法)处理“冲突”:把所有“同义词”存储在一个链表中。

例如：

优化：在插入新元素时，保持关键字有序，可微微提高查找效率。

2.散列查找

• 最理想情况:散列查找时间复杂度可到达O(1)。
• 装填因子α=表中记录数/散列表长度。
• 装填因子会直接影响散列表的查找效率。

3.常见散列函数的设计

散列函数的设计要结合实际的关键字分布特点来考虑，不要教条化。

对给定的关键字集合,应尽可能均匀地散列到各个地址，使冲突更少。

1.除留余数法

$H(key)=(key)mod(p)$
散列表表长为m，取一个不大于m但最接近或等于m的质数p.

• 质数又称素数。指除了1和此整数自身外,不能被其他自然数整除的数.
• 用质数取模。分布更均匀，冲突更少。

2.直接定址法

$H(key)=key或H(key)=a\ast key+b$

• 其中，a和b是常数。这种方法计算最简单，且不会产生冲突。
• 它适合关键字的分布基本连续的情况，
• 若关键字分布不连续，空位较多，则会造成存储空间的浪费。

3.数字分析法

选取数码分布较为均匀的若干位作为散列地址.

• 设关键字是r进制数〈如十进制数)，而r个数码在各位上出现的频率不一定相同，可能在某些位上分布均匀一些，每种数码出现的机会均等;
• 而在某些位上分布不均匀，只有某几种数码经常出现，此时可选取数码分布较为均匀的若干位作为散列地址。
• 这种方法适合于已知的关键字集合，若更换了关键字，则需要重新构造新的散列函数。

4.平方取中法

取关键字的平方值的中间几位作为散列地址.

• 具体取多少位要视实际情况而定。
• 这种方法得到的散列地址与关键字的每位都有关系，因此使得散列地址分布比较均匀，
• 适用于关键字的每位取值都不够均匀或均小于散列地址所需的位数。

散列查找是典型的“用空间换时间”的算法，只要散列函数设计的合理，则散列表越长，冲突的概率越低。

4.处理冲突的方法2：开放地址法

所谓开放定址法，是指可存放新表项的空闲地址既向它的同义词表项开放，又向它的非同义词表项开放。其数学递推公式为∶
$$Hi=(H(key)+di)mod(m)$$
$i=0,1,\mathrm{2...},k(k\le m-1)$,m表示散列表表长;di为增量序列;
i可理解为“第i次发生冲突”

关于增量序列$di$的设计有：

1.线性探测法

$di=0,1,2,3,...,m-1;$
即发生冲突时，每次往后探测相邻的下一个单元是否为空 .

1.查找操作
空位置的判断也要算作一次比较。
越早遇到空位置，就可以越早确定查找失败。

2.删除操作
注意:采用“开放定址法"时，删除结点不能简单地将被删结点的空间置为空，否则将截断在它之后填入散列表的同义词结点的查找路径，可以做一个“删除标记”，进行逻辑删除。

3.查找效率分析
弊端：当第一次冲突位置离目标较远时，看起来很满，实际上很空，花费较长的时间。

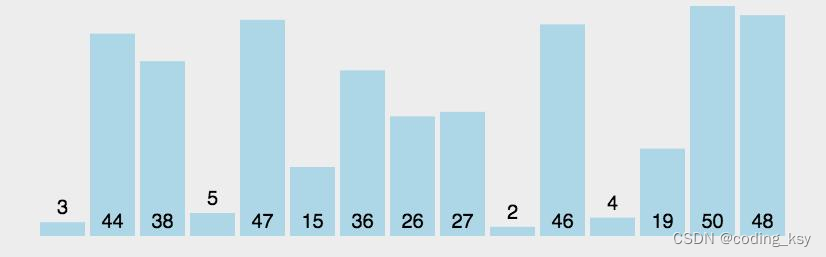
初次探测的地址 Ho只有可能在$[0,12]$

线性探测法很容易造成同义词、非同义词的“聚集（堆积)”现象，严重影响查找效率。
产生原因——冲突后再探测一定是放在某个连续的位置。

2.平方探测法

当$di=0^2,1^2,-1^2,2^2,-2^2,....k^2,-k^2$时，称为平方探测法，
又称二次探测法其中$k\le m/2$

• 平方探测法:比起线性探测法更不易产生“聚集（堆积)”问题。
• 非重点小坑:散列表长度m必须是一个可以表示成4j+3的素数，才能探测到所有位置。(数论)

3.伪随机序列法

di是一个伪随机序列，如di= 0,5,24,11,…

5.处理冲突的方法3:再散列法

再散列法（再哈希法)︰除了原始的散列函数H(key)之外，
多准备几个散列函数，当散列函数冲突时，
用下一个散列函数计算一个新地址，直到不冲突为止:
$H=RHi(Key)i=1,2,\mathrm{3....},k$