Problem: 18. 四数之和

解题思路

讲述看到这一题的思路

• 首先我们来分析一下本题的思路：这题和我们之前所讲过的一题叫做 三数之和，与本题非常得类似，如果没有做过的扣友可以先去做做看
• 那我们来分析一下本题的题意，题目中说到会给我们一个整数数组nums和一个目标值target，这和三数之和不同的是这四个数相加之和要为target，而且这个四元组不可以重复
• 那我们来看示例1，从[1, 0, -1, 0, -2, 2]这几个数里面找到了三组符合条件的四元组

💬 那具体这个寻找的过程是怎样的呢，我们一起看下去

算法原理分析

马上我们就来说说这个算法的实现原理

对于【暴力解法】我在 三数之和 里面已经说过了，肯定会造成超时的现象，所以我直接来介绍双指针的解法：

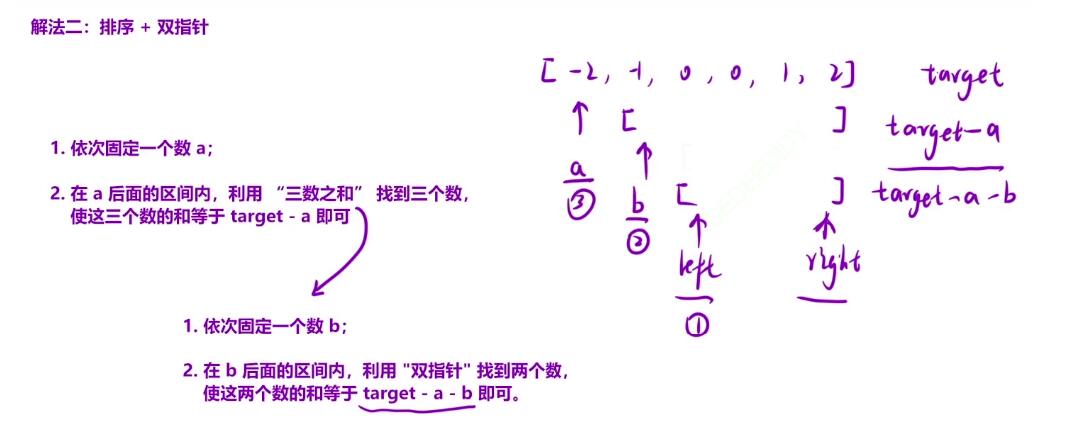
• 首先我们要先固定的就是最前面的这个数a，接下去的话就是在后面的这段区间中找到三个数，它们的和为target - a的

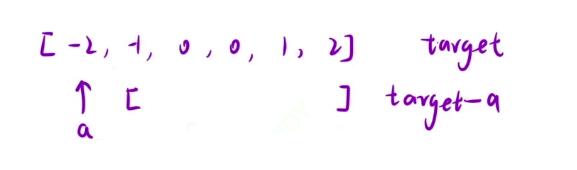
• 但是呢三个数相加我们无法去做到很好的定位，因为我们是要使用双指针来解决这道题，所以呢对于后面的小区间我们还要再做一个划分：继续定位出来最前面的一个数作为数b，然后在后面的区间中找到两个数之和等于target - a - b

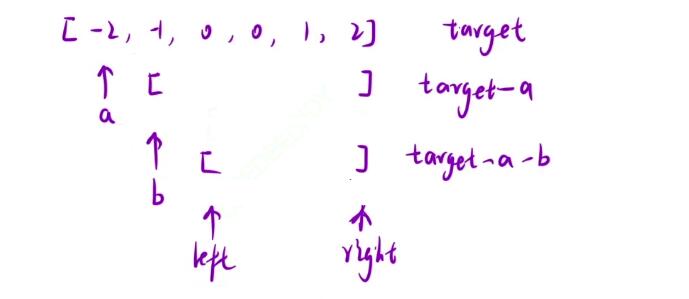
• 但是呢我们除了考虑一些基本的要求外，还需要去考虑到去重和越界的问题，在这里我们不仅是要考虑到left和right，而且还需要考虑到在外侧所固定的数a和数b

💬 所以，光就这么分析来看，本题的难度是要大于【三数之和】的，所以读者可以试着自己写写看代码，锻炼提升一下自己💪

复杂度

• 时间复杂度:

对于时间复杂度, 最外层固定一个数a，然后遍历; 第二层遍历一个数b，然后接着遍历，在最内层呢我们通过while循环继续去做遍历，那么这个时间复杂度即为 $O(n^3)$

• 空间复杂度:

因为没有开出任何额外的空间，所以空间复杂度为 $O(n)$

Code

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        // 1.排序
        sort(nums.begin(), nums.end());

        // 2.利用双指针解决问题
        int n = nums.size();
        vector<vector<int>> result;
        for(int i = 0;i < n; )      // 固定a
        {
            // 利用三数之和进行求解
            for(int j = i + 1;j < n; )      // 固定b
            {
                int left = j + 1, right = n - 1;
                long long targetSum = (long long)target - nums[i] - nums[j];
                while(left < right)
                {
                    int sum = nums[left] + nums[right];
                    if(sum < targetSum){
                        left++;
                    }else if(sum > targetSum){
                        right--;
                    } 
                    else{
                        // 将找到的数据放入结果集中
                        result.push_back({nums[i], nums[j], nums[left++], nums[right--]});

                        // left和right去重
                        while(left < right && nums[left] == nums[left - 1]) left++;
                        while(left < right && nums[right] == nums[right + 1]) right--;
                    }
                }
                // j去重
                j++;
                while(j < n && nums[j] == nums[j - 1])  j++;
            }
            // i去重
            i++;
            while(i < n && nums[i] == nums[i - 1])  i++;            
        }
        return result;
    }
};