(一)传送门:
[刷题记录]牛客面试笔刷TOP101(一)_HY_PIGIE的博客-CSDN博客
目录
1.合并二叉树
2.二叉树的镜像
3.判断是否为二叉搜索树
4.判断是不是完全二叉树
1.合并二叉树
合并二叉树_牛客题霸_牛客网 (nowcoder.com)
思路:
在后序遍历的基础上进行,两颗二叉树可能会有位置有空缺的情况.
在一个子树下,拿到了左节点与右节点并在根节点下进行操作->后序遍历
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
// write code here
//如果是两个都是空的也无所谓,相互返回空就好了
if(t1 == null){
return t2;
}
if(t2 == null){
return t1;
}
//创建一个合并的新节点作为根节点
TreeNode root = new TreeNode(t1.val + t2.val);
//进行后序遍历
TreeNode left = mergeTrees(t1.left,t2.left);
TreeNode right = mergeTrees(t1.right,t2.right);
//拼装
root.left = left;
root.right = right;
return root;
}2.二叉树的镜像
二叉树的镜像_牛客题霸_牛客网 (nowcoder.com)
思路:
分别交换每一颗子树的左右节点,采用后序遍历的方式
public TreeNode Mirror (TreeNode pRoot) {
// write code here
if(pRoot == null){
return null;
}
//镜像就是交换每一颗子树的左右节点
//那就要先拿到其左右节点
//可以使用后序遍历的方式,后序遍历为:左右根
//当来到根的时候,已经分别拿到了两个节点
//再分别将他们交换位置即可
TreeNode left = Mirror(pRoot.left);
TreeNode right = Mirror(pRoot.right);
pRoot.left = right;
pRoot.right = left;
return pRoot;
}3.判断是否为二叉搜索树
判断是不是二叉搜索树_牛客题霸_牛客网 (nowcoder.com)
思路:
二叉搜索树:左节点<根<右节点.
可以结合下面这一题一起看
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)
二叉搜索树的中序遍历则是一个递增的序列,当判断一颗二叉树是否为二叉搜索树时只要判断其中序遍历得到的数值是否为递增就好了.
既然要比较,就要用到两个指针.
一个指针指向当前遍历的节点,还有一个指针记录上一个节点的数值.进行比较后移位.
错解:
忘记更新pre了....
int pre = Integer.MIN_VALUE;
public boolean isValidBST (TreeNode root) {
// write code here
if(root == null){
return true;
}
//遍历左子树
boolean left = isValidBST(root.left);
//判断前驱的数值与当前节点的数值关系
if(pre > root.val){
return false;
}
boolean right = isValidBST(root.right);
return left && right;
}正解:
int pre = Integer.MIN_VALUE;
public boolean isValidBST (TreeNode root) {
// write code here
if(root == null){
return true;
}
//遍历左子树
boolean left = isValidBST(root.left);
//判断前驱的数值与当前节点的数值关系
if(pre > root.val){
return false;
}
//更新一下pre
pre = root.val;
//遍历右子树
boolean right = isValidBST(root.right);
return left && right;
}4.判断是不是完全二叉树
判断是不是完全二叉树_牛客题霸_牛客网 (nowcoder.com)
思路:
完全二叉树,不是满二叉树.
完全二叉树要求可以单独有左节点,但不能单独有右节点.
满二叉树是除了叶子节点,每一个节点都有左右节点.
使用层序遍历的方式,遍历二叉树放到队列中.
当遇到空节点时将其存放,并判断后面的节点是否为空,如果后面的节点不为空则判断其不是完全二叉树
public boolean isCompleteTree (TreeNode root) {
// write code here
//层序遍历
//如果有左节点但没有右节点就返回false
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean left = true;
while(!queue.isEmpty()){
//当队列不为空时
TreeNode tmp = queue.poll();
//当遇到空节点时
if(tmp == null){
left = false;
}else{//如果当前节点不为空,判断前一个节点是否为空
if(left == false){//如果前一个节点为空,且当前节点不为空
return false;//返回false;
}
//如果前一个节点与后一个节点都不为空
//把其的左右节点加入
queue.offer(tmp.left);
queue.offer(tmp.right);
}
}
return true;
}5.判断是不是平衡二叉树
判断是不是平衡二叉树_牛客题霸_牛客网 (nowcoder.com)
思路:
递归的思想,判断每一个根节点的左右子树的高度差.
public boolean IsBalanced_Solution (TreeNode pRoot) {
// write code here
//从上到下递归遍历
//查看每一颗树的左右深度差
if(pRoot == null){
return true;
}
int left = deep(pRoot.left);
int right = deep(pRoot.right);
if(left - right > 1 || left - right < -1){
return false;
}
return IsBalanced_Solution(pRoot.left) && IsBalanced_Solution(pRoot.right);
}
public int deep(TreeNode root){
if(root == null){
return 0;
}
int left = deep(root.left);
int right = deep(root.right);
return left < right ? right + 1 : left + 1;
}6.二叉搜索树的最近公共祖先
二叉搜索树的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)
思路:
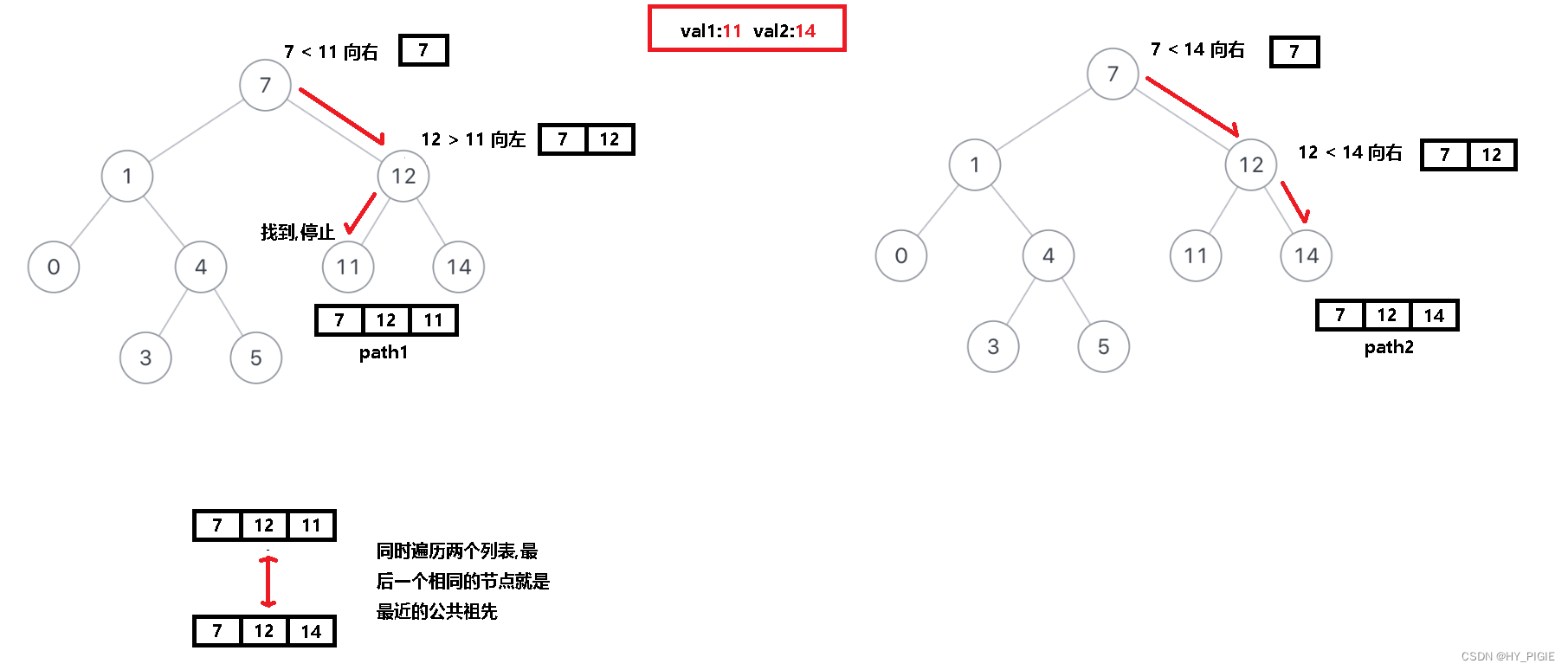
先遍历找到两个目标节点,并使用列表来记录所遍历的节点.
因为是二叉搜索树,所以遍历的思路与二维数组查找的思路很相似,当前节点的val小于目标节点时走向右节点,反之向左节点.直至找到目标节点.
再一起遍历两个路径列表,在列表中的最后一个相同的节点就是最近的公共祖先.
public List<Integer> path(TreeNode root,int val){
List<Integer> ret = new ArrayList<>();
while(root != null){
ret.add(root.val);
if(root.val == val){
break;
}
if(root.val < val){
root = root.right;
}else{
root = root.left;
}
}
return ret;
}
public int lowestCommonAncestor (TreeNode root, int p, int q) {
// write code here
//前提是二叉搜索树
//首先得找到两个特定的节点
//并使用列表来记录路径
//当当前节点比目标节点大时,走左节点.反之走右节点
List<Integer> path1 = path(root,p);
List<Integer> path2 = path(root,q);
//一起遍历两个列表
int len1 = path1.size();
int len2 = path2.size();
int ret = 0;
for(int i = 0 ; i < len1 && i < len2; i++){
int tmp1 = path1.get(i);
int tmp2 = path2.get(i);
if(tmp1 == tmp2){
ret = tmp1;
}else{
break;
}
}
return ret;
}7.在二叉树中找到两个节点的最近公共祖先
在二叉树中找到两个节点的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)
思路:
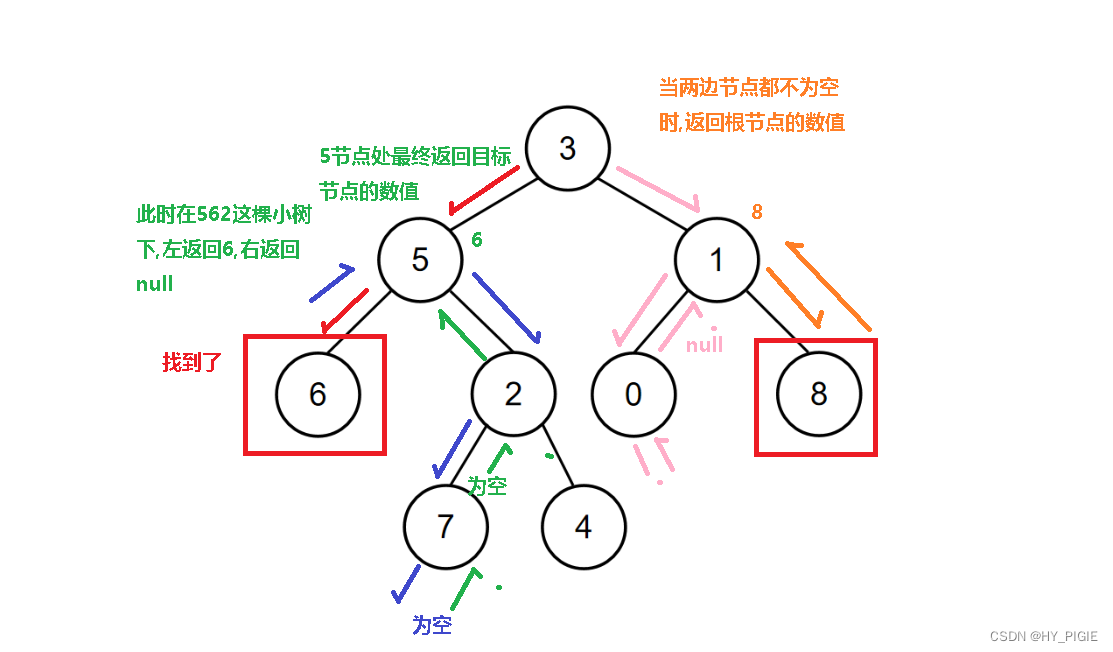
使用递归先来找到特定的节点.
如果两个目标节点在同一颗小树下,则直接返回根节点.
如果当前小树只有左节点或右节点为目标节点则返回当前的目标节点.
public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
// write code here
if(root == null){
return -1;
}
if(root.val == o1 || root.val == o2){
return root.val;
}
int left = lowestCommonAncestor(root.left,o1,o2);
int right = lowestCommonAncestor(root.right,o1,o2);
if(left == -1){
return right;
}
if(right == -1){
return left;
}
return root.val;
}