文章目录
- 题目
- 方法一:把该题当做一个普通的二叉树来做(任何遍历都可以)
- 方法二:利用完全二叉树的性质来做
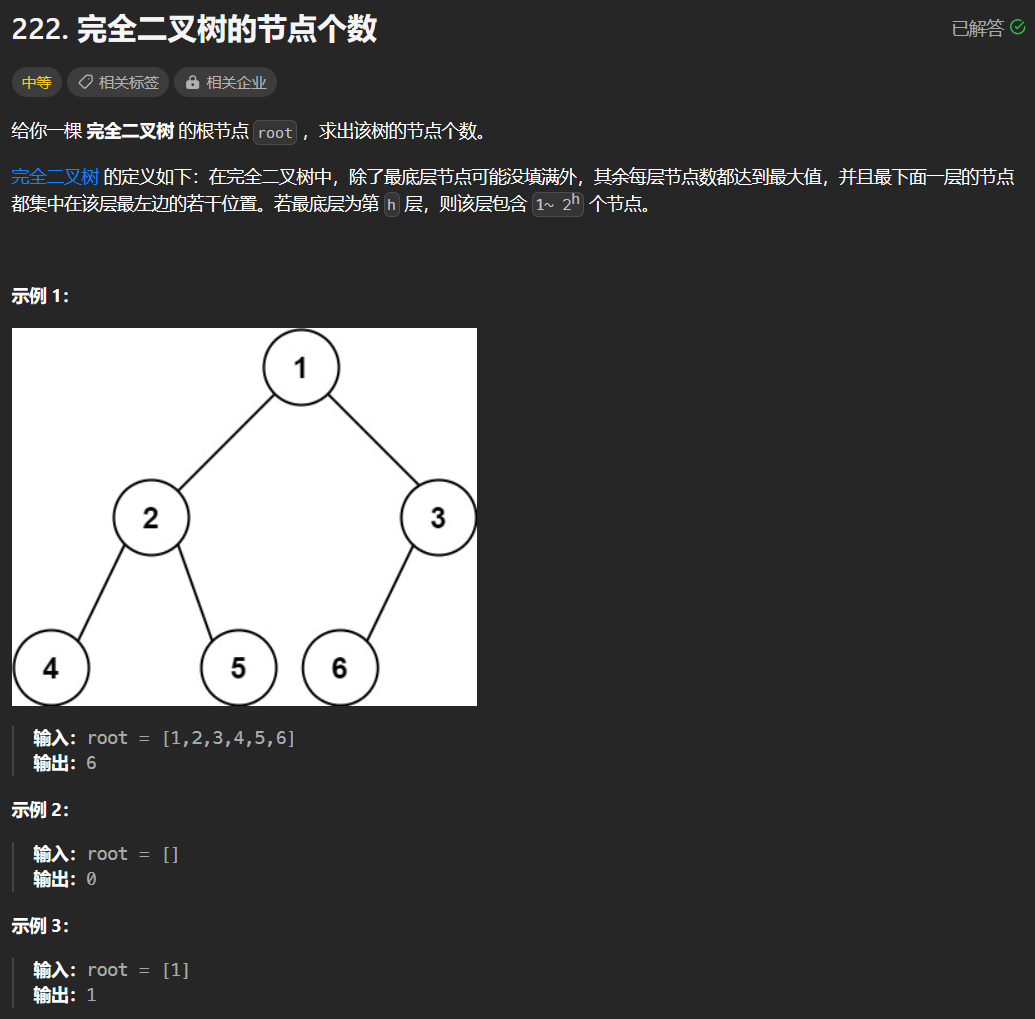
题目
方法一:把该题当做一个普通的二叉树来做(任何遍历都可以)
例如:二叉树的前序遍历(维护一个全局变量)递归无返回值
class Solution {
int num = 0;
public int countNodes(TreeNode root) {
dfs(root);
return num;
}
public void dfs(TreeNode root){
if(root == null) return;
num++;
dfs(root.left);
dfs(root.right);
}
}
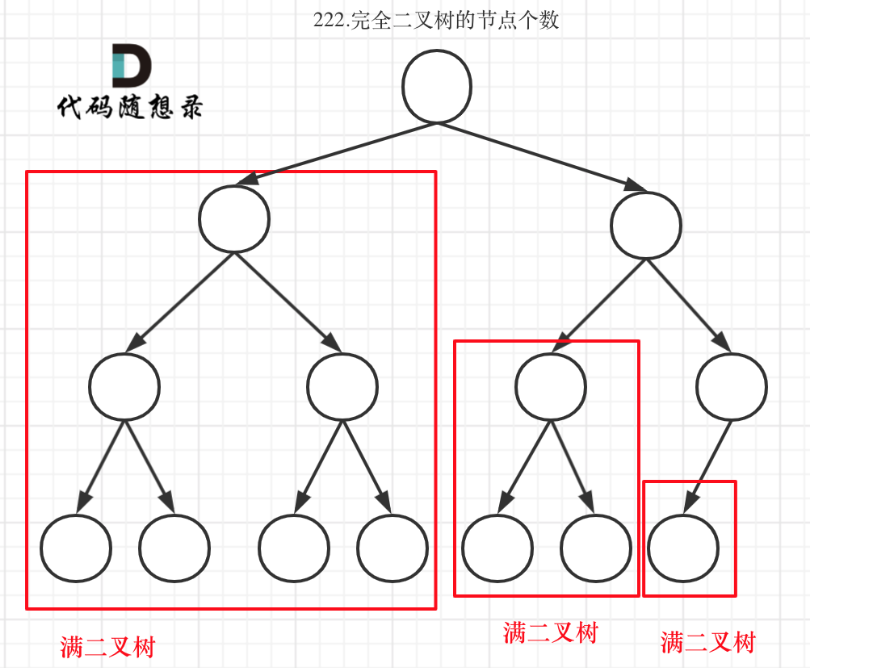
方法二:利用完全二叉树的性质来做
- 当前节点只要满足完全二叉树的话,可以通过2^depth-1来计算以当前节点为父节点的数的节点数,这样减少很多递归操作,不需要递归找到每一个节点
- 当前节点不满足二叉树的性质 ,那就走常规递归到下一层,再来判断
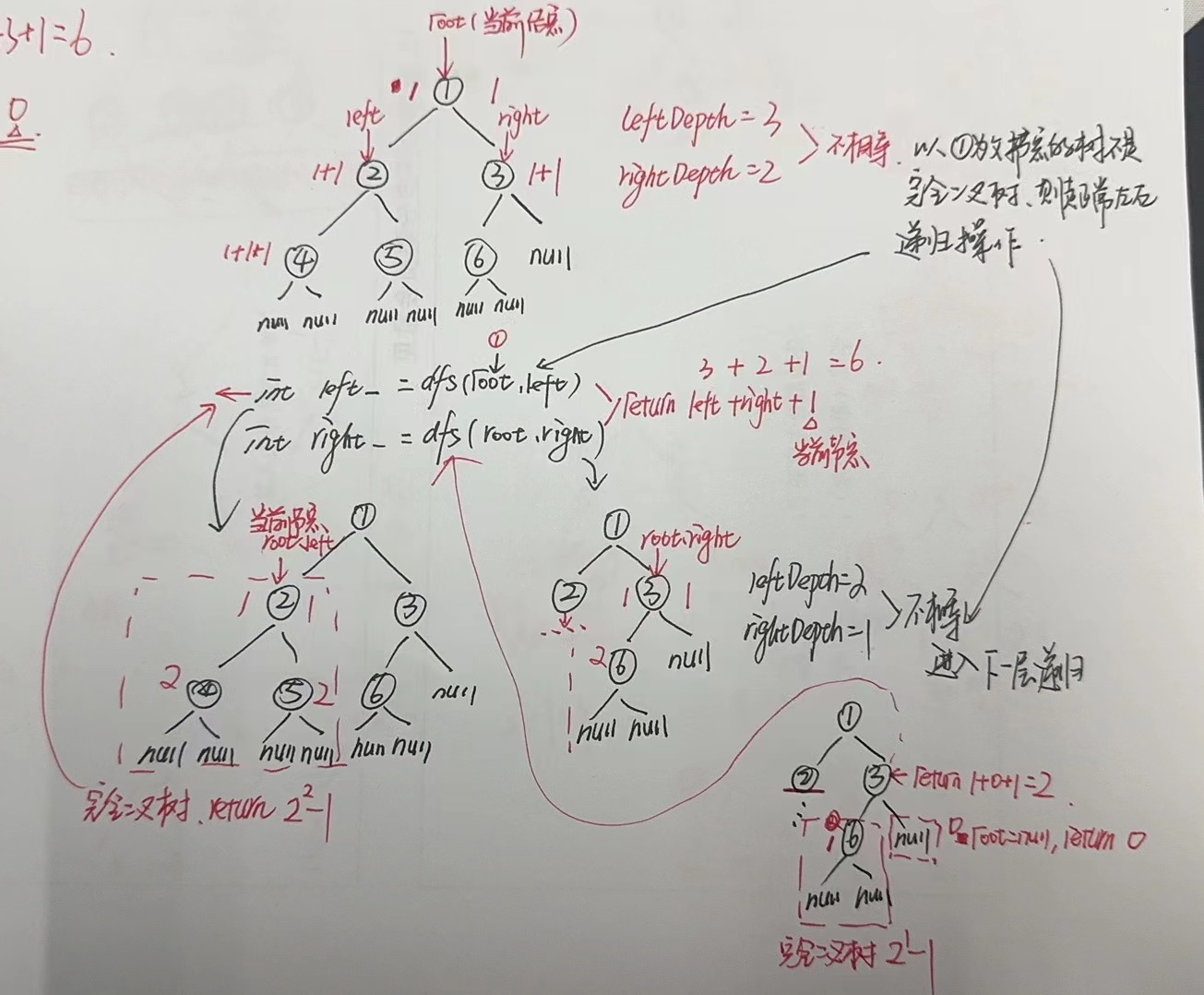
一定要画图 模拟递归过程
lass Solution {
public int countNodes(TreeNode root) {
return dfs(root);
}
public int dfs(TreeNode root){
if(root == null) return 0;
int leftsum = 1;//root不为null 自然高度起始就是1
int rightsum = 1;
TreeNode left = root.left;
TreeNode right = root.right;
//寻找以该节点为父节点的左右子树的高度
while(left!=null){
left = left.left;
leftsum++;
}
while(right!=null){
right = right.right;
rightsum++;
}
//如果左右子树的高度相等 说明以该节点为父节点的数是完全二叉树 ,所以可以按照完全二叉树的性质来计算节点数 2的高度次方-1
if(rightsum == leftsum) return (int)Math.pow(2, rightsum) - 1;
//如果左右子树的高度不相等 那么进入下一层常规递归
int left_ = dfs(root.left);
int right_ = dfs(root.right);
return left_+right_+1;//最后返回左右子树节点数之和在加上本节点
}
}