1.B树的插入
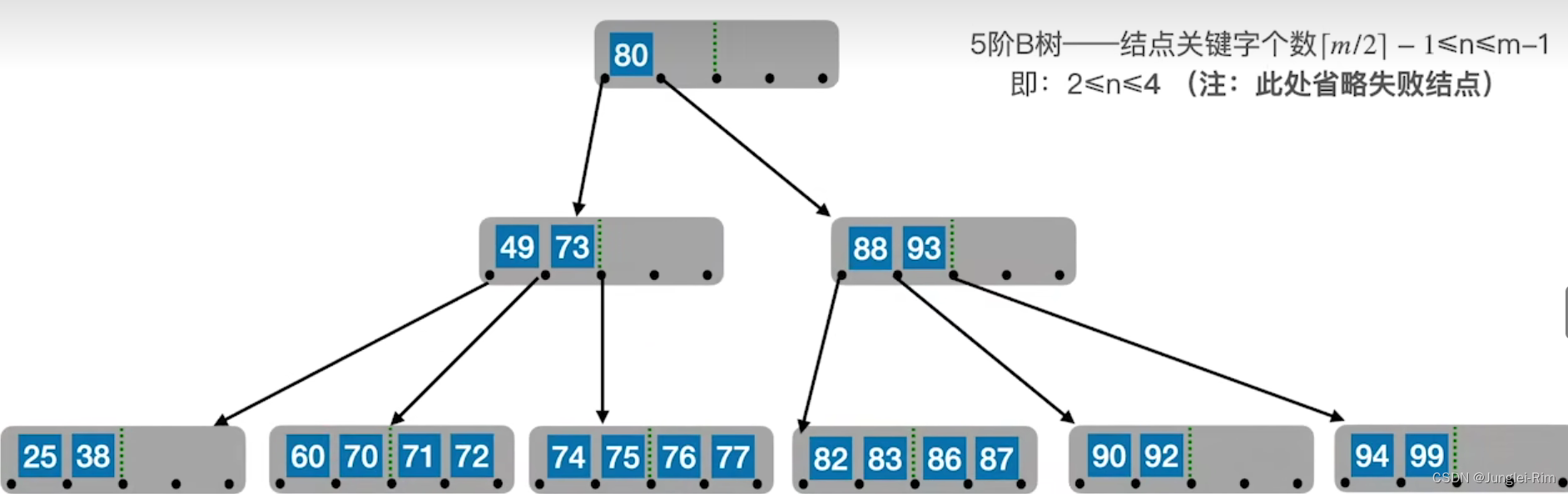
1.核心要求
- 对m阶B树——除根节点外,结点关键字个数 [ m / 2 ] − 1 ≤ n ≤ m − 1 [m/2] -1≤n≤m-1 [m/2]−1≤n≤m−1
- 子树0<关键字1<子树1<关键字2<子树2<…
新元素一定是插入到最底层“终端节点”,用“查找”来确定插入位置.
2.具体步骤
若插入后结点关键字个数未超过上限,则无需做其他处理.
- 在插入key后,若导致原结点关键字数超过上限,则从中间位置([m/2])将其中的关键字分为两部分,
- 左部分包含的关键字放在原结点中,
- 右部分包含的关键字放到新结点中,
- 中间位置([m/2])的结点插入原结点的父结点.
- 若此时导致其父结点的关键字个数也超过了上限,则继续进行这种分裂操作,
- 直至这个过程传到根结点为止,进而导致B树高度增1。
2.B树的删除
1.终端结点关键字
- 若被删除关键字在终端节点,则直接删除该关键字(要注意节点关键字个数是否低于下限[m/2]-1)
2.非终端结点关键字
- 若被删除关键字在非终端节点,则用直接前驱或直接后继来替代被删除的关键字,
- 直接前驱︰当前关键字左侧指针所指子树中“最右下”的元素。
- 直接后继:当前关键字右侧指针所指子树中“最左下”的元素
- (与二叉排序树中查找直接前驱和直接后继是一致的)
- 对非终端结点关键字的删除,必然可以转化为对终端的结点的删除操作。
3.当终端结点的低于当前分支的下限时:
1.兄弟够借。
若被删除关键字所在结点删除前的关键字个数低于下限且与此结点右(或左)兄弟结点的关键字个数还很宽裕,则需要调整该结点、右(或左)兄弟结点及其双亲结点(父子换位法)。
具体操作:
- 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺。
- 当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺
- 本质:要永远保证子树O<关键字1<子树1<关键字2<子树2<…
2.兄弟不够借。
若被删除关键字所在结点删除前的关键字个数低于下限,且此时与该结点相邻的左、右兄弟结点的关键字个数均=[m/2] -1,则将关键字删除后与左(或右)兄弟结点及双亲结点中的关键字进行合并。
具体操作:
- 在合并过程中,双亲结点中的关键字个数会减1。
- 若其双亲结点是根结点且关键字个数减少至0(根结点关键字个数为1时,有2棵子树),则直接将根结点删除,合并后的新结点成为根;
- 若双亲结点不是根结点,且关键字个数减少到[m/2]-2,则又要与它自己的兄弟结点进行调整或合并操作,并重复上述步骤,直至符合B树的要求为止。









![计算机视觉与深度学习-全连接神经网络-训练过程-模型正则与超参数调优- [北邮鲁鹏]](https://img-blog.csdnimg.cn/a9e2d73ad52c4b94a751d208e1c4a9ce.png)