蒙特卡洛方法的数学基础-1

news2024/9/28 15:23:03

蒙特卡洛方法的数学基础-1

概率论

Bayes 公式

$P(A_i|B)=\frac{P(A_iB)}{P(B)}=\frac{P(B|A_i)P(A_i)}{\sum_j P(B|A_j)P(A_j)}$

常用分布

Binominal Distribution

$\begin{matrix} P(k)=\frac{N!}{k!(N-k)!}p^k(1-p)^{N-k}\\ E(k)=Np\\ D(k)=Np(1-p) \end{matrix}$

Poisson Distribution

$\begin{matrix} P(k)=\frac{\lambda^k}{k!}e^{-k}\\ E(k)=\lambda\\ D(k)=\lambda \end{matrix}$

Gaussian Distribution $N(X;\mu,\sigma)$

$\begin{matrix} f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}}\\ \\ \end{matrix}$

$P(a\leq x\leq b)=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma})=2\Phi(\frac{b-\mu}{\sigma})-1$

Exponential Distribution

$\begin{matrix} f(x)=\frac{1}{\lambda}e^{-x/\lambda}\\ F(z)=1-e^{-z/\lambda}\\ \end{matrix}$

Uniform Distribution

$\begin{matrix} f(x)=\frac{1}{a-b}\\ E(x)=\frac{a+b}{2}\\ D(x)=\frac{(b-a)^2}{12} \end{matrix}$

大数定理

均匀概率分布随机地取N个数xi ，函数值之和的算术平均收敛于函数的期望值
算术平均收敛于真值

$E(\bar{x})=E(x)=\mu$

中心极限定理

n个相互独立分布各异的随机变量的总和服从正态分布
置信水平下的统计误差

$N(\mu,\sigma^2)=\frac{1}{\sigma \sqrt{2\pi}}exp[\frac{-(x-\mu)^2}{2\sigma^2}]$

$D(\bar{x})=\frac{D(x)}{N}=\frac{\sigma^2}{N}$

Monte Carlo方法简单应用

案例：Buffon 投针实验

案例：投点法求定积分

任意分布的伪随机变量的抽样

反函数直接抽样法

$\begin{matrix} 0\leq F(x)=\int_{-\infty}^x f(x)dx \leq 1\\ def:\zeta =F(\eta) \\ \eta = F^{-1}(\zeta) \end{matrix}$

变换抽样法

dim=1

$\begin{matrix} f(x)dx=g(y)dy\\ g(y)=f(x^{-1}(y))\cdot \begin{Vmatrix} \frac{dx}{dy} \end{Vmatrix} \end{matrix}$

dim=2

$\begin{matrix} x=g_1(u,v)\,\,\,\ y=g_2(u,v)\\ f(x,y)=g(u(x,y),v(x,y))\cdot \begin{Vmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{Vmatrix} \end{matrix}$

改进的Maraglia方法

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

Num = 10000
x = np.zeros(Num)
y = np.zeros(Num)
z = np.zeros(Num)

Times = 0
while Times < Num:
    u,v = np.random.rand(2)
    w = (2*u-1)**2 + (2*v-1)**2
    if w<=1:
        z[Times] = (-2*np.log(w)/w)**0.5        
        x[Times] = u * z[Times]
        y[Times] = v * z[Times]
        Times += 1
    else:
        continue

fig = plt.figure(figsize=(12, 6))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

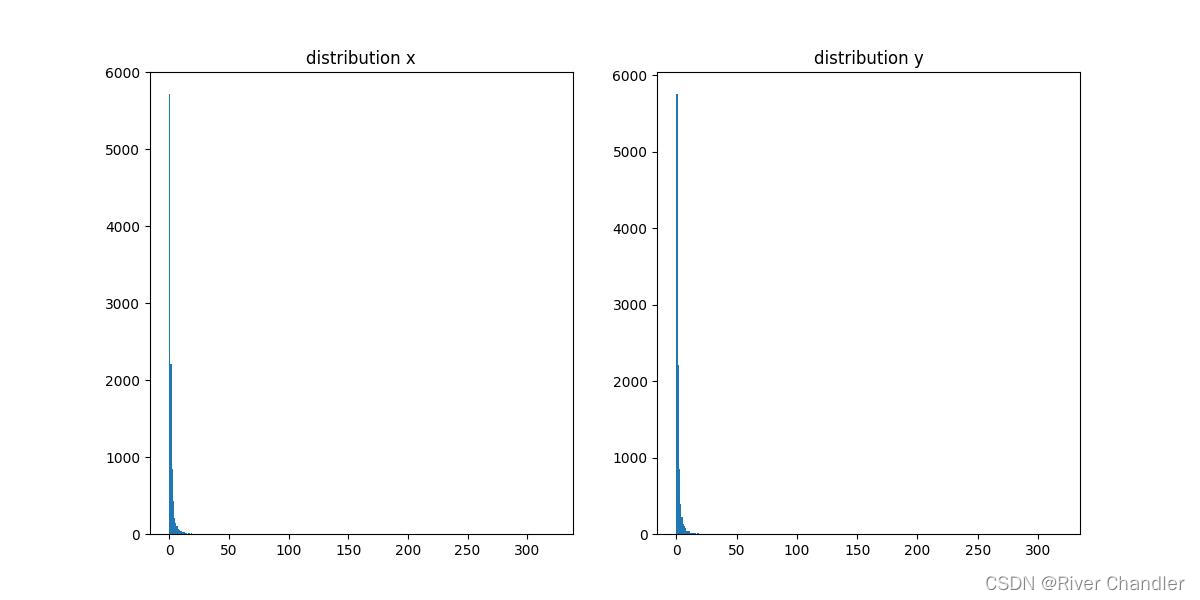
ax1.hist(x, np.arange(0, max(x), 1))
ax1.set_title("distribution x")

ax2.hist(y, np.arange(0, max(y), 1))
ax2.set_title("distribution y")

plt.savefig("3.jpg")

舍选抽样法

...

复合抽样法

$f(x)=\int_{-\infty}^{+\infty}g(x|y)h(y)dy$

依据概率密度函数 $h(y)$ 抽样 $y_h$
依然条件概率密度函数 $g(x|y_h)$ 抽样 $x_g$

$\zeta_f=x_{g(x|y_h)}$

加分布与减分布抽样法

加分布抽样

$f(x)=\sum_nh_n(x)p_n$ 其中 $0<p_n<1,\sum_np_N=1,\int_{-\infty}^{+\infty}h_n(x)=1$

取\zeta \sim U[0,1]，解对n的不等式

$\sum_{i=1}^{n-1}p_i < \zeta \leq \sum_{i=1}^np_i$

对，对应的hn(x) 抽样得 \zeta = \zeta_{h_n}

减分布抽样

乘加与乘减分布抽样法

...

反函数近似抽样法

近似替代 $F^{-1}(y)\approx Q(y)$

最小二乘拟合 $F^{-1}(y)\approx Q(y)=a+by+cy^2+\alpha (1-y)^2lny+\beta y^2ln(1-y)$

极限近似法

...

蒙特卡洛方法处理定积分

近似积分公式

近似积分公式在某种意义上是对区间内某些函数值的加权平均
- 蒙卡方法的目的是优化样本点的选择（位置和权重）
矩形积分方法(The Leftpoint Rule)
- 1阶近似
矩形积分方法(The Rightpoint Rule)
- 1阶近似
矩形积分方法(The Midpoint Rule)
- 2阶近似
梯形积分方法(The Trapezoidal Rule)
- 2阶近似
Simpson's Rule
- 4阶近似

蒙特卡洛积分思路

iid
- independent and identically distributed

$\begin{matrix} I=\int_a^b g(x)dx\\ I=(b-a)\int_a^b g(x)\frac{dx}{b-a}\\ I=(b-a)<g(x)>,x\sim U[a,b]\\ I\approx(b-a)\frac{\sum_ig(x_i)}{N} \end{matrix}$

$\begin{matrix} I=(b-a)(\tilde{y}\pm \frac{\tilde{S}}{\sqrt{N}})\\ I=\tilde{I}\pm \tilde{\sigma}(\tilde{I}) \end{matrix}$

example

$\int_a^b (x^2+e^x )dx$

import matplotlib.pyplot as plt
import numpy as np
import scipy.integrate as integrate

np.random.seed(0)
a = 0
b = 5
N = 100000

f = lambda x:x**2 + np.exp(x)
result1 = integrate.quad(f, a, b)

points = np.random.rand(N)*(b-a) + a
ybar = sum(f(points))/N
Sbar = (sum((points-ybar)**2)/N)**0.5 
result2 = ((b-a)*ybar, (b-a)*Sbar/N**0.5)

X = np.linspace(a, b, N+1)
result3 = f(X[0]) + f(X[N])
flag = 1
for i in range(1, N-1):
    if flag == 1:
        result3 += 4*f(X[i])
        flag *= -1
        
    elif flag == -1:
        result3 += 2*f(X[i])
        flag *= -1

    else:
        print("ERROR!")
        
result3 *= (b-a)/N/3

print("result1:", result1)
print("result2:", result2)
print("result3:", result3)

result1: (189.07982576924329, 2.099207760611269e-12)
result2: (188.98624801068067, 0.5586055984291508)
result3: 189.06826542000084
>>>

如何评价哩，只能说，蒙卡方法至少能积出正确的答案，关键是速度慢啊
好吧，有人说是代码写得差，嗯合理
改一下

import matplotlib.pyplot as plt
import numpy as np
import scipy.integrate as integrate

np.random.seed(0)
a = 0
b = 5
N = 100000

f = lambda x:x**2 + np.exp(x)
result1 = integrate.quad(f, a, b)

points = np.random.rand(N)*(b-a) + a
ybar = sum(f(points))/N
Sbar = (sum((points-ybar)**2)/N)**0.5 
result2 = ((b-a)*ybar, (b-a)*Sbar/N**0.5)

X = np.linspace(a, b, N+1)
result3 = f(X)
coeff = np.ones(N+1)
coeff[1::2] = 4
coeff[2::2] = 2
result3 *= coeff
result3 = sum(result3)

        
result3 *= (b-a)/N/3

print("result1:", result1)
print("result2:", result2)
print("result3:", result3)

测一下用时吧，时间复杂度都是同阶的（大误，这是Python的numpy 特性）

import matplotlib.pyplot as plt
import numpy as np
import scipy.integrate as integrate
import time

np.random.seed(0)
a = 0
b = 5
N = 100000

f = lambda x:x**2 + np.exp(x)
s1 = time.time()
for i in range(100):
    result1 = integrate.quad(f, a, b)
e1 = time.time()

s2 = time.time()
for i in range(100):
    points = np.random.rand(N)*(b-a) + a
    ybar = sum(f(points))/N
    Sbar = (sum((points-ybar)**2)/N)**0.5 
    result2 = ((b-a)*ybar, (b-a)*Sbar/N**0.5)
e2 = time.time()

X = np.linspace(a, b, N+1)
coeff = np.ones(N+1)
coeff[1::2] = 4
coeff[2::2] = 2
s3 = time.time()
for i in range(100):
    result3 = f(X)
    result3 *= coeff
    result3 = sum(result3)
    result3 *= (b-a)/N/3
e3 = time.time()

print("result1:", result1, "used time:", round(e1 - s1, 2))
print("result2:", result2, "used time:", round(e2 - s2, 2))
print("result3:", result3, "used time:", round(e3 - s3, 2))

result1: (189.07982576924329, 2.099207760611269e-12) used time: 0.0
result2: (188.83626394308098, 0.5580722224407848) used time: 1.8
result3: 189.0827159885614 used time: 0.9
>>>