机器学习西瓜书+南瓜书吃瓜教程第三章学习笔记

本次学习为周老师的机器学习西瓜书+谢老师南瓜书+Datawhale视频
视频地址

下面为本人的学习笔记，最近很忙还没学多少，之后补！！！
u1s1，边看视频边自己手推一遍真的清楚很多，强烈推荐自己手推虽然花时间，但真的很有用很清晰

线性模型

- 1、基本形式
- 2、最小二乘估计&&极大似然估计
- 3、求解w和b
- 4、举例

机器学习是想要通过现有的数据，找到隐藏在事物背后的规律。
而大部分规律是符合线性模型的形式
为了能进行数学运算，样本中的非数值类属性都需要进行数值化。
机器学习三要素：
1.模型：根据具体问题，确定假设空间
2.策略：根据评价标准，确定选取最优模型的策略（通常会产出一个“损失函数”）
3.算法：求解损失函数，确定最优模型

1、基本形式

给定由d个属性描述的示例在这里插入图片描述
其中xi是x在第i个属性上的取值，线性模型试图学的一个通过属性的线性组合来进行预测的函数，即：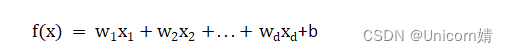
一般用向量形式写成

其中w = (w1;w2;…;wd),模型就得以确定。

2、最小二乘估计&&极大似然估计

在这里插入图片描述

极大似然估计的直观想法：使得观测样本出现概率最大的分布就是待求分布，也就是使得联合概率（似然函数）L( $\theta$ )取得最大值的 $\theta$ 即为 $\theta$ 的估计值。
在这里插入图片描述

3、求解w和b

凸集介绍：向下凹的函数叫凸函数，相当于数学里面最优化的思路
在这里插入图片描述
梯度：多元函数的一阶导数

列向量为分母布局，行向量为分子布局。求梯度即为求偏导数。
Hessian（海塞）矩阵（多元函数的二阶导数）：

其本质上是一个多元函数求最值点的问题，更具体点是凸函数求最值的问题
推导思路：
1、证明 $E\left( w,b\right) =\sum ^{m}_{i=1}\left( y_{i}-wx_{i}-b\right) ^{2}$ 是关于w和b的凸函数。
2、用凸函数求最值的思路求解出w和b。
在这里插入图片描述

半正定矩阵的判定定理之一：
若实对称矩阵的所有顺序主子式均为非负，则该矩阵为半正定矩阵。
在这里插入图片描述
好的到这里我们已经完成了第一步证明，接下来我们要完成第二步证明即用凸函数求最值的思路求解出w和b。

这边手写忘拍照啦，就写一下思路吧~
首先令对b的一阶导等于0，可以求出b，为了后续求解方便首先将b化简，再对令的一阶导等于0，然后把b代进去算…
从几何的角度，让全体训练样本经过投影后：

异类样本的中心尽可能远
同类样本的方差尽可能小
对数几率回归算法的机器学习三要素：
1.模型：线性模型，
输出值的范围为,近似阶跃的单调可微函数
2.策略：
极大似然估计，信息论
3.算法：
梯度下降，牛顿法

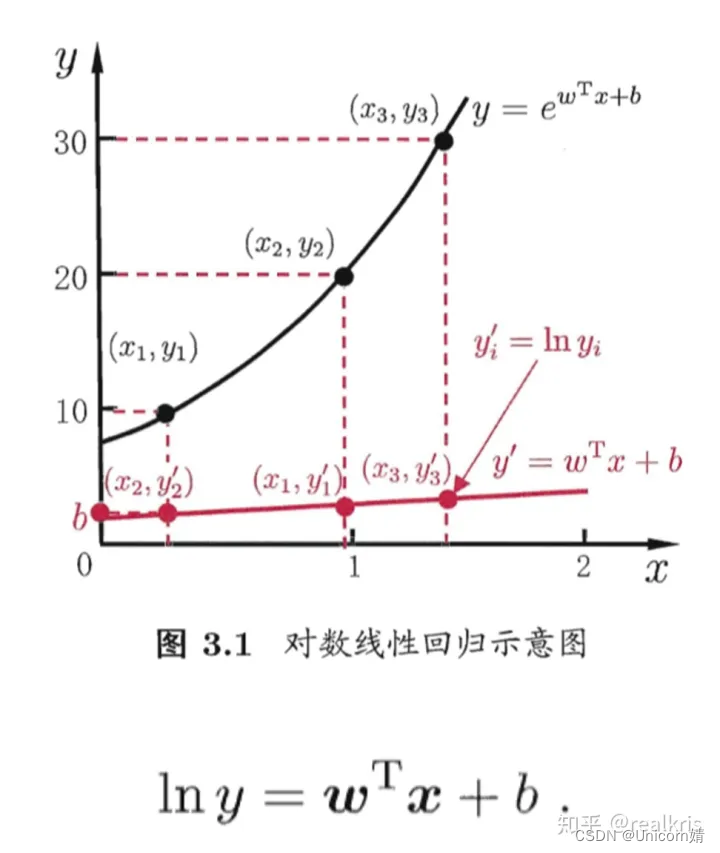
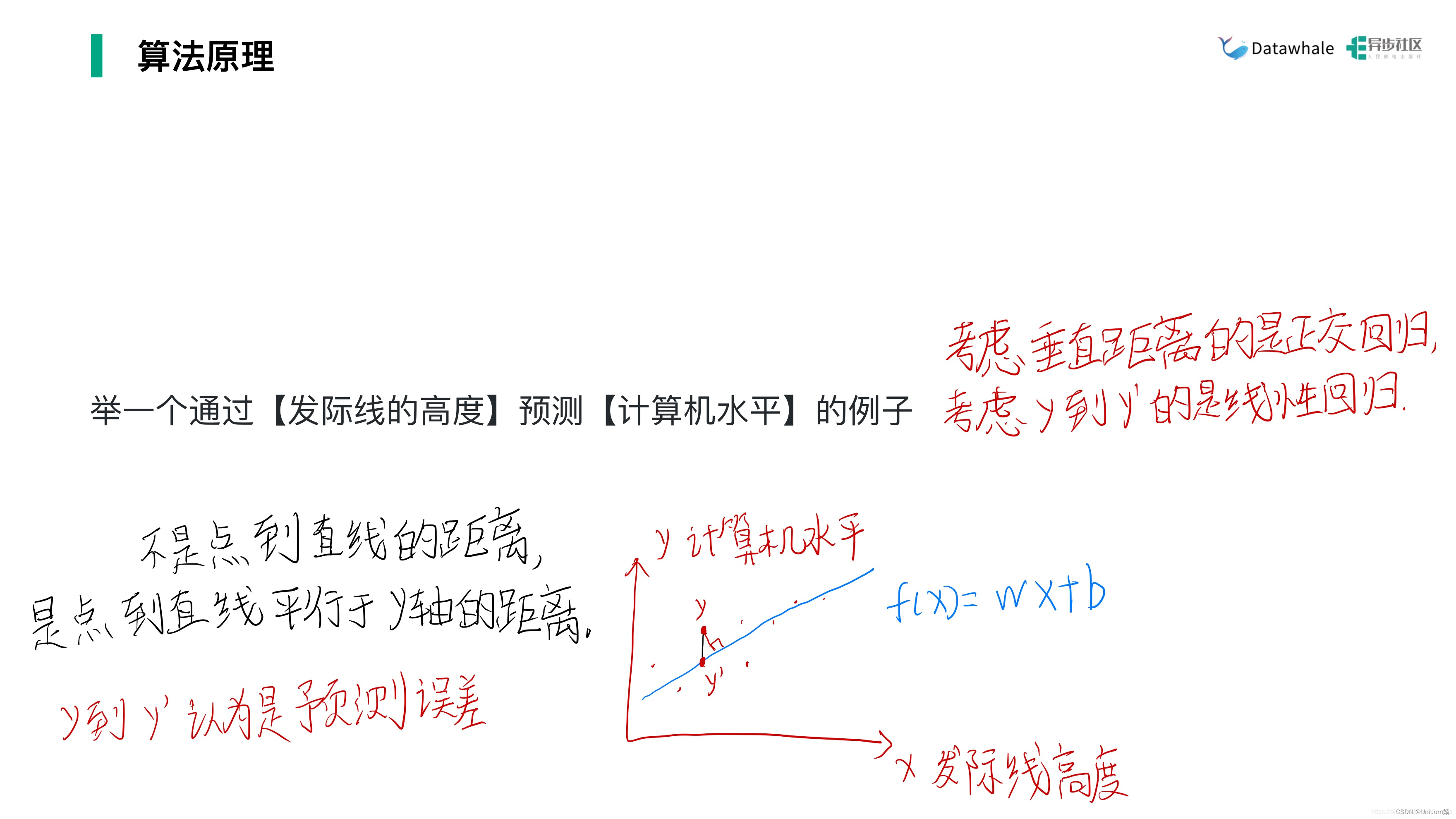
它实际是让ewTx+b逼近y，虽然形式上是线性回归，但是实际是求取输入空间到输出空间的非线性函数映射。这里的对数函数起到了将线性回归模型的预测值与真实标记相联系的作用。

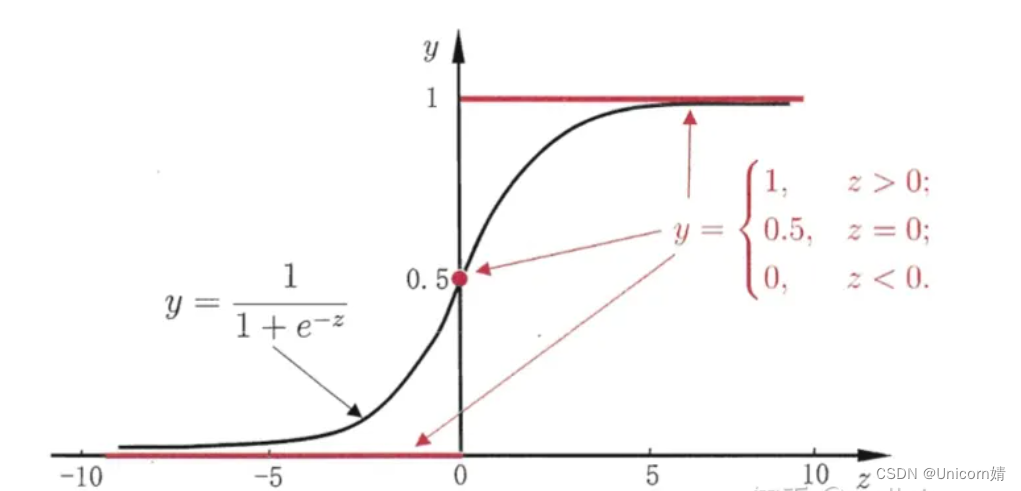
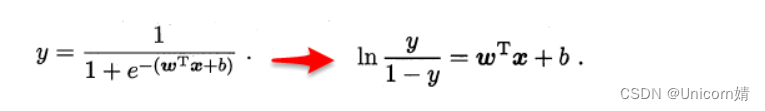
在这里插入图片描述

若将y视为x为正例的可能性，1-y为其为反例的可能性，两者的比值为x为正例的相对可能性。对于几率取对数得到的就是“对数几率”。对数几率回归也叫逻辑回归。
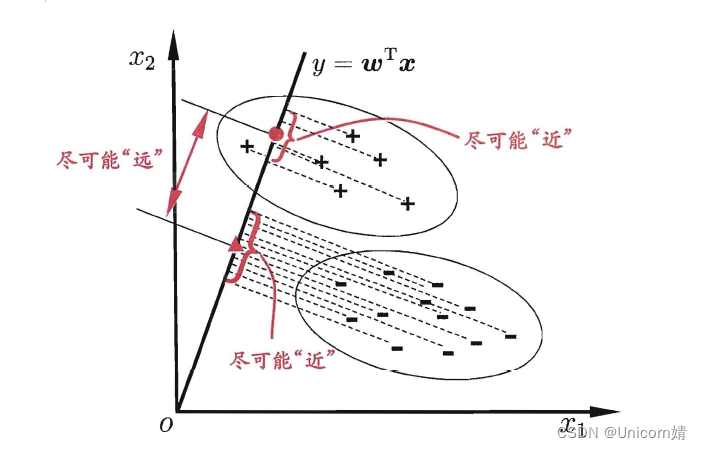
线性判别分析（Linear Discriminant Analysis，简称LDA）,其基本思想是：将训练样本投影到一条直线上，使得同类的样例尽可能近，不同类的样例尽可能远。如图所示：
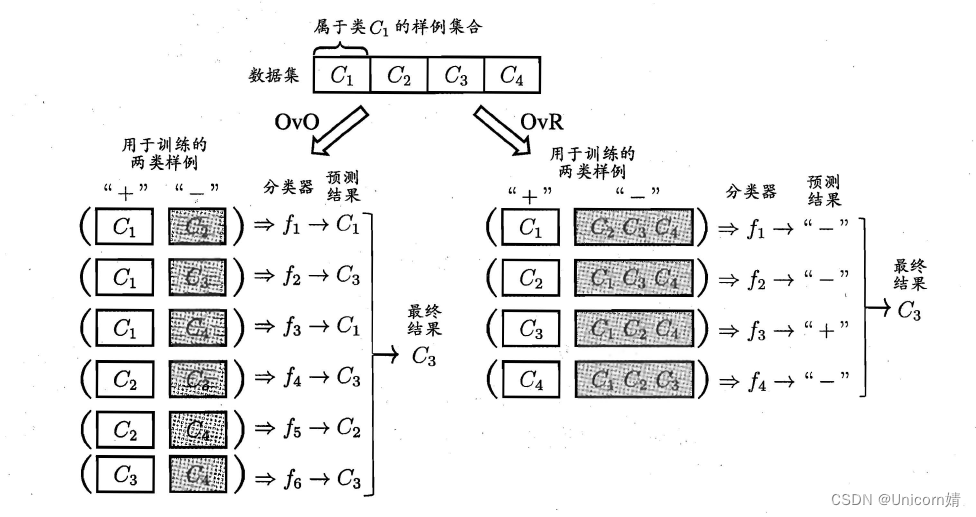
在这里插入图片描述

现实中我们经常遇到不只两个类别的分类问题，即多分类问题，在这种情形下，我们常常运用“拆分”的策略，通过多个二分类学习器来解决多分类问题，即将多分类问题拆解为多个二分类问题，训练出多个二分类学习器，最后将多个分类结果进行集成得出结论。最为经典的拆分策略有三种：“一对一”（OvO）、“一对其余”（OvR）和“多对多”（MvM），核心思想与示意图如下所示。
👉基于一些基本策略，利用二分类学习器来解决多分类问题
·“一对一”（One vs.One，简称OvO）
·“一对其余”（One vs.Rest，简称OvR）
·“多对多”（Many vs.Many，简称MvM）
OvO：给定数据集D，假定其中有N个真实类别，将这N个类别进行两两配对（一个正类/一个反类），从而产生N（N-1）/2个二分类学习器，在测试阶段，将新样本放入所有的二分类学习器中测试，得出N（N-1）个结果，最终通过投票产生最终的分类结果。

OvM：给定数据集D，假定其中有N个真实类别，每次取出一个类作为正类，剩余的所有类别作为一个新的反类，从而产生N个二分类学习器，在测试阶段，得出N个结果，若仅有一个学习器预测为正类，则对应的类标作为最终分类结果。

MvM：给定数据集D，假定其中有N个真实类别，每次取若干个类作为正类，若干个类作为反类（通过ECOC码给出，编码），若进行了M次划分，则生成了M个二分类学习器，在测试阶段（解码），得出M个结果组成一个新的码，最终通过计算海明/欧式距离选择距离最小的类别作为最终分类结果。
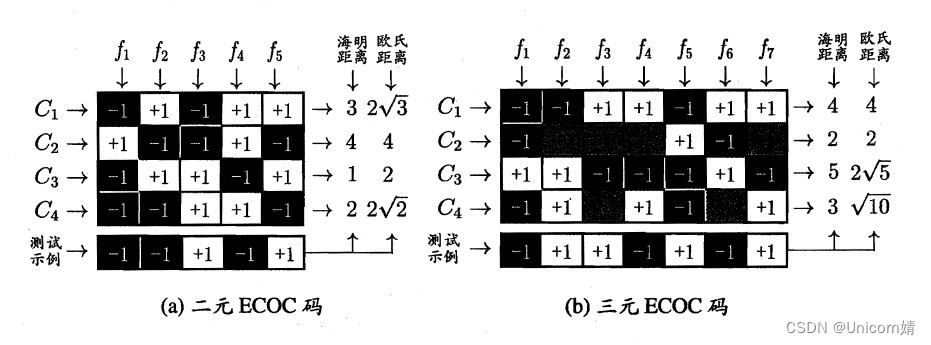
在这里插入图片描述

在这里插入图片描述
类别不平衡（class-imbanlance）就是指分类问题中不同类别的训练样本相差悬殊的情况，例如正例有900个，而反例只有100个，这个时候我们就需要进行相应的处理来平衡这个问题。常见的做法有三种：

在训练样本较多的类别中进行“欠采样”（undersampling）,比如从正例中采出100个，常见的算法有：EasyEnsemble。
在训练样本较少的类别中进行“过采样”（oversampling）,例如通过对反例中的数据进行插值，来产生额外的反例，常见的算法有SMOTE。
直接基于原数据集进行学习，对预测值进行“再缩放”处理。其中再缩放也是代价敏感学习的基础。
欠采样：去除一些反例使得正、反例数目接近
·过采样：增加一些正例使得正、反例数目接近
·阈值移动：直接基于原始数据集进行学习，但是预测时改变预测为正例的阈值（不再为0.5）

4、举例

1、sklearn中的线性回归
sklearn中的线性回归模型如下：

from sklearn.linear_model import LinearRegression
sklearn.learn_model.LinearRegression()

它表示最小二乘线性回归，线性回归拟合具有系数w = (w1,…,wp)的线性模型，以最小化数据集中观察到的目标与通过线性近似预测的目标之间的残差平方和，它的完整参数如下：

sklearn.linear_model.LinearRegression(fit_intercept=True,normalize=False,copy_X=True)

参数解释：

fit_intercept,是否计算此模型的截距，默认True，如果设置为False，则不会在计算中使用截距
normalize：数据标准化，默认为False，官方给的建议是用StandardScaler，
copy_X:如果为True，则X将被复制；否则，它可能会被覆盖、默认为True。
参数解释：
fit(X,y[,sanmple_weight]):拟合线性模型（也可以叫做训练线性模型）
predict(X):使用线性模型进行预测。
score(X,y[,sample_weight]):返回预测的确定系数，即R^2.
2、案例实现：价格预测
假设有例子，x和y分别表示某面积和总价，需要根据面积来预测总价。
第一步导入模块：

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

第二步:导入数据并绘制散点图

#创建数据
x = np.array([6,16,26,36,46,56]).reshape((-1,1))
y = np.array([4,23,10,12,22,35])

plt.scatter(x,y)#绘制散点图
plt.show()

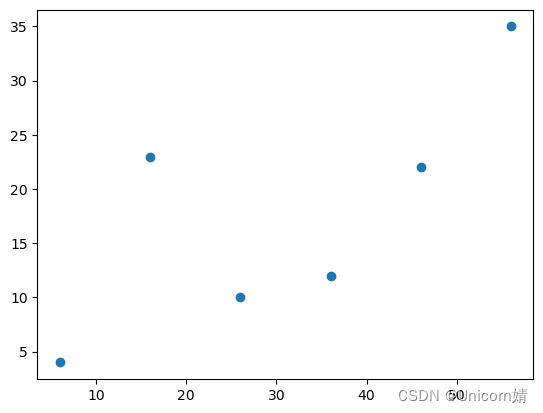
在这里插入图片描述

第三步：创建模型并拟合

model = LinearRegression().fit(x,y)

第四步：评估模型

r_sq = model.score(x,y)
print('确定系数:',r_sq)

确定系数: 0.5417910447761195
第五步：获取线性回归模型中的参数

#打印截距
print('截距：',model.intercept_)

#打印斜率
print('斜率：',model.coef_)

#预测一个响应并打印它：
y_pred = model.predict(x)
print('预测结果：',y_pred,sep='\n')

截距： 4.026666666666664
斜率： [0.44]
预测结果：
[ 6.66666667 11.06666667 15.46666667 19.86666667 24.26666667 28.66666667]
3、销售预测
数据集如下：
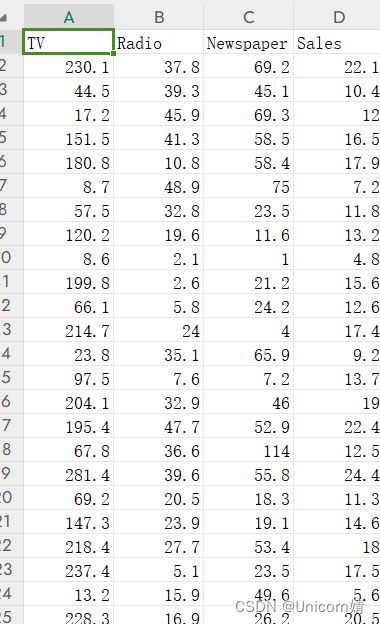
在这里插入图片描述
分别表示：

TV：电视台
Radio：广播
Newspaper: 报纸
sales: 销售价格
第一步：读取数据并展示数据

import pandas as pd
data=pd.read_csv(r"D:\advertising.csv")
data

如图：
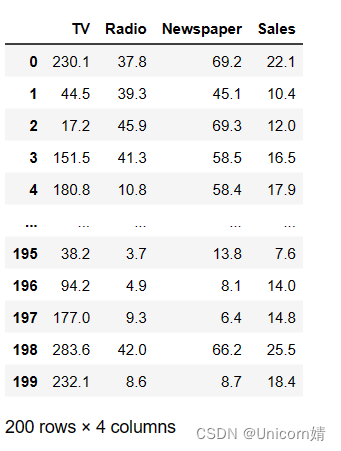
在这里插入图片描述
回归方程别忘了：y = c+m1x1+m2x2+…+mn*xn

y是预测值，是因变量
c是截距
m1是第一个特征
m2是第二个特征
m3是第三个特征
mn是第n个特征
在这里我们只做电视和销售的关系，因此方程为：y = c+m1xTV
第二步：提取自变量和因变量

X = data['TV'].values.reshape(-1,1)#使其成为数组
y = data['Sales'].values

第三步：分隔训练集和测试集。将70%的数据保留在训练数据集中，其余30%保留在测试数据集中。

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,test_size=0.3,random_state=100)

第四步：数据可视化

plt.scatter(X_train,y_train,color='purple')
plt.xlabel('x ')
plt.ylabel('y ')
plt.title("Scatter Plot")
plt.show()

如图：
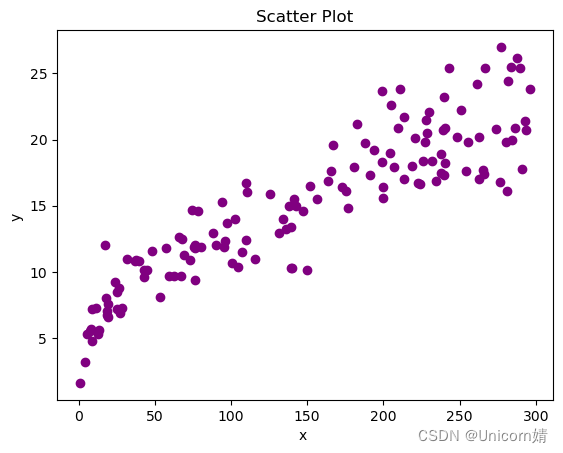
在这里插入图片描述
第五步：建立线性回归模型

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

第六步：训练模型并使用选项回归模型预测

lr.fit(X_train,y_train)
y_predict = lr.predict(X_test)

第七步：评估模型使用训练精确度和测试精确度。可以根据这两个指标判断是否过拟合还是欠拟合，训练精度大于测试精度则过拟合，如果两者都很小就是欠拟合。

print(f'Training accuracy:{round(lr.score(X_train,y_train)*100,2)}%')
print(f'Testing accuracy:{round(lr.score(X_test,y_test)*100,2)}%')

输出：

Training accuracy:81.58%
Testing accuracy:79.21%

4、线性回归优缺点
优点：

建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。
可以根据系数给出每个变量的理解和解释。
缺点:
不能很好地拟合非线性数据，所以需要先判断变量之间是否为线性关系。
南瓜书地址