文章目录
- 一、函数
- 1.函数的概念、基本初等函数
- 2.函数的性质 /函数四性态
- 1.单调性
- 2.奇偶性
- (3)导函数的奇偶性
- 3.周期性
- 4.有界性
- 5.对称性
- 3.基本不等式
- 4.开根要带绝对值
- 二、极限
- 1.极限的概念
- ①数列极限
- ②函数极限
- 需要区分左右极限的三种问题 (左右极限有区别,需要分)
- 2.极限的性质
- ①有界性
- ②保号性
- ③极限值与无穷小的关系
- 3.极限的存在准则
- ①单调有界准则
- ②夹逼定理
- 4.无穷小量
- (1)无穷小量阶的比较
- 5.无穷大量
- (1)无穷大比阶
- (2)无界函数 vs 无穷大量
- 6.求极限(求极限的方法)
- 1.利用有理运算法则求极限
- 2.基本极限求极限 (两个重要极限)
- 3.利用等价无穷小代换求极限
- (1)代换原则:乘除关系、加减关系
- (2)常见等价无穷小
- (3)变上限积分的等价代换
- 4.利用洛必达法则求极限
- 5.利用泰勒公式求极限
- 6.利用夹逼准则求极限
- 7.定积分定义求极限
- 8.利用单调有界准则求极限
- 7.求函数极限的7种未定式
- 三、连续
- 1.连续性的概念
- 2.间断点
- (1)间断点的定义
- (2)间断点的分类
- 3.连续性的运算与性质
- 4.闭区间上连续函数的性质
- 1.有界性与最大最小值定理
- 2.介值定理
- 3.零点定理
- 5.总结
- (1)连续与可导
- (2) 连续与极限
- (3) 极限需要注意的问题:求极限,能否直接代入的问题
- (4) 方程根的存在性及个数
一、函数
1.函数的概念、基本初等函数
1.函数
是否是同一个函数:看定义域和对应法则f,是否相同。与字母(记号)无关。
2.复合函数
3.反函数:若g(x)是f(x)的反函数,则:
①
g
(
f
(
x
)
)
=
x
g(f(x))=x
g(f(x))=x
②
g
′
(
x
)
=
1
f
(
x
)
,
g
′
′
(
x
)
=
−
f
′
′
(
x
)
[
f
′
(
x
)
]
3
g'(x)=\dfrac{1}{f(x)},g''(x)=-\dfrac{f''(x)}{[f'^(x)]^3}
g′(x)=f(x)1,g′′(x)=−[f′(x)]3f′′(x)
①定义:【f是定义域到值域的一一映射】对于每一个y,都有唯一的x与之对应。则有反函数。
②如何求反函数:①反解 y=f(x) ->x=g(y) ②x与y调换,写成y=g(x)。则f与g互为反函数
4.基本初等函数
①幂:
x
a
x^a
xa
②指:
y
=
a
x
y=a^x
y=ax (a>0,a≠1)
③对:
y
=
l
o
g
a
x
y=log_ax
y=logax (a>0,a≠1)
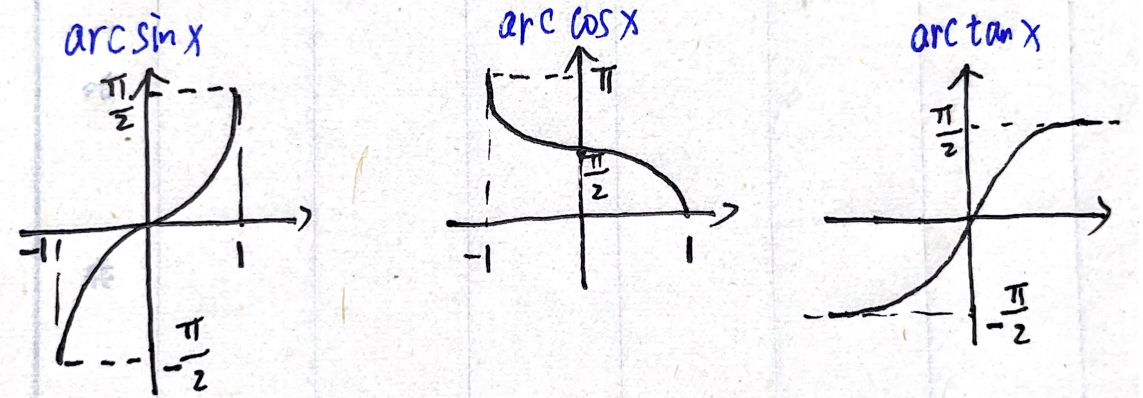
④三角:sinx cosx tanx
⑤反三角函数:arcsinx arccosx arctanx
arcsin
x
+
arccos
x
=
π
2
\arcsin x+\arccos x=\dfrac{π}{2}
arcsinx+arccosx=2π
Ⅰ.arcsinx,定义域
[
−
1
,
1
]
[-1,1]
[−1,1],值域 [
−
π
2
-\dfrac{π}{2}
−2π,
π
2
\dfrac{π}{2}
2π]
arcsin
1
2
=
π
6
\arcsin \dfrac{1}{2}=\dfrac{π}{6}
arcsin21=6π
θ
∈
(
0
,
π
2
)
,
a
r
c
s
i
n
(
s
i
n
θ
)
=
θ
θ∈(0,\dfrac{π}{2}),arcsin(sinθ)=θ
θ∈(0,2π),arcsin(sinθ)=θ
θ
∈
(
π
2
,
π
)
,
a
r
c
s
i
n
(
s
i
n
θ
)
=
π
−
θ
θ∈(\dfrac{π}{2},π),arcsin(sinθ)=π-θ
θ∈(2π,π),arcsin(sinθ)=π−θ
Ⅱ.arccosx,定义域[-1,1],值域 [- π 2 \frac{π}{2} 2π, π 2 \frac{π}{2} 2π]
初等函数:
由五类基本初等函数经过有限次的 加减乘除和复合 运算后,且能用一个解析式表示的函数,称为初等函数。
2.函数的性质 /函数四性态
单调性、奇偶性、周期性、有界性 +对称

1.单调性
(1)
f
(
x
)
单增⇦⇨
f
′
(
x
)
≥
0
f(x)单增 ⇦⇨ f'(x)≥0
f(x)单增⇦⇨f′(x)≥0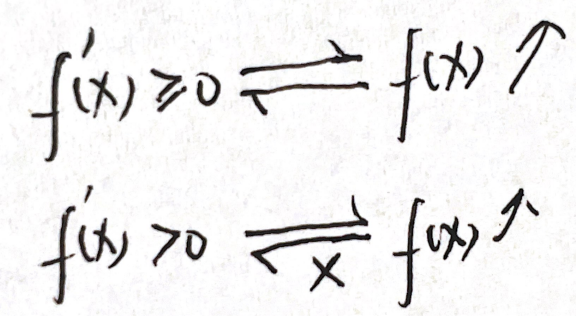
(2)f每多一个负号,单调性发生变化:f(x)单增,则f(-x)单减,-f(-x)单增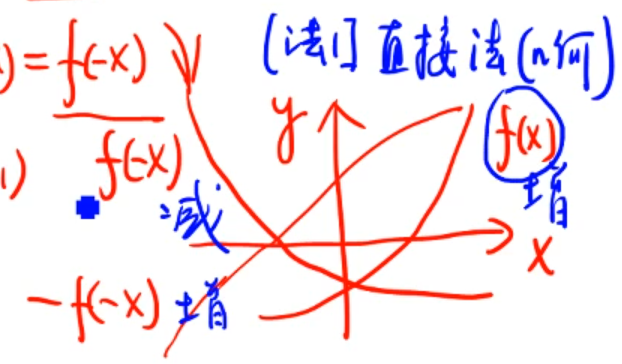
例题1:武钟祥老师每日一题 24.Day62 单调性

答案:D
2.奇偶性
(1)奇函数:
①定义:
f
(
−
x
)
=
−
f
(
x
)
f(-x)=-f(x)
f(−x)=−f(x)
②性质:i.奇函数关于原点对称 ii.若奇函数在x=0处有定义,则f(0)=0
(2)偶函数
①定义:
f
(
−
x
)
=
f
(
x
)
f(-x)=f(x)
f(−x)=f(x)
②性质:
Ⅰ.偶函数关于y轴对称
Ⅱ.
f
(
x
)
+
f
(
−
x
)
f(x)+f(-x)
f(x)+f(−x)为偶函数
(3)导函数的奇偶性
F(x)为f(x)的原函数:
①F(x)为奇函数 ⇨ f(x)为偶函数
②F(x)为偶函数 ⇦⇨ f(x)为奇函数

(4)
f
(
∣
x
∣
)
与
∣
f
(
x
)
∣
f(|x|)与|f(x)|
f(∣x∣)与∣f(x)∣:
①
f
(
∣
x
∣
)
f(|x|)
f(∣x∣)是关于x的偶函数,左右对称
②
∣
f
(
x
)
∣
=
∣
y
∣
|f(x)|=|y|
∣f(x)∣=∣y∣是关于y的偶函数,上下对称
例题1:22年数三 周期性、奇偶性
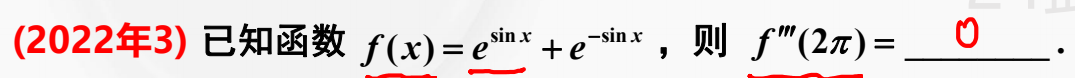
分析:
①f(x+2π)=f(x) ∴f(x)为T=2π的周期函数 ∴f’‘’(x)也为T=2π的周期函数 ∴f’‘’(2π)=f’‘’(0)
②f(x)=g(x)+g(-x)为偶函数,则偶函数在0点的奇次阶导数为0
答案:0
例题2:07年3.
f
(
x
)
f(x)
f(x)为奇函数,则
F
(
x
)
F(x)
F(x)为偶函数

答案:C
例题3:19年12.
∣
y
∣
|y|
∣y∣是关于y的偶函数
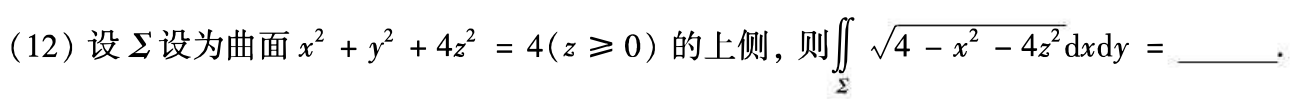
分析:

答案: 32 3 \dfrac{32}{3} 332
3.周期性
1.定义:
f
(
x
+
T
)
=
f
(
x
)
f(x+T)=f(x)
f(x+T)=f(x),则f(x)为周期函数
2.性质:
①设f(x)连续且以T为周期,则
F
(
x
)
=
∫
0
x
f
(
t
)
d
t
F(x)=\int_0^xf(t)dt
F(x)=∫0xf(t)dt 是以T为周期的周期函数 ⇦⇨
∫
0
T
f
(
x
)
d
x
=
0
\int_0^Tf(x)dx=0
∫0Tf(x)dx=0
②周期函数的原函数是周期函数 ⇦⇨(充要条件) 其在一个周期上的积分为零
③若F(x)是以T为周期的可导函数,则
F
′
(
x
)
=
f
(
x
)
F'(x)=f(x)
F′(x)=f(x)仍是以T为周期的周期函数
④设f(x)是以T为周期的连续函数,则
∫
a
a
+
T
f
(
x
)
d
x
=
∫
0
T
f
(
x
)
d
x
=
∫
−
T
2
T
2
f
(
x
)
d
x
\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx=\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)dx
∫aa+Tf(x)dx=∫0Tf(x)dx=∫−2T2Tf(x)dx ,
∫
0
n
T
f
(
x
)
d
x
=
n
∫
0
T
f
(
x
)
d
x
\int_0^{nT}f(x)dx=n\int_0^Tf(x)dx
∫0nTf(x)dx=n∫0Tf(x)dx


例题1:660 T212
例题2:18年18(2)
4.有界性
1.有界性的定义:
有界,既有上界,又有下界

2.有界性的判定:

5.对称性
1.对称区间上,奇函数积分为0,偶函数积分为正半区间的2倍
2.①
f
(
x
)
f(x)
f(x)与
f
(
−
x
)
f(-x)
f(−x)关于
y
轴对称
y轴对称
y轴对称
②
f
(
x
)
f(x)
f(x)与
−
f
(
x
)
-f(x)
−f(x)关于
x
轴对称
x轴对称
x轴对称
3. f ( x + a ) f(x+a) f(x+a)与 f ( x − a ) f(x-a) f(x−a)关于 x = a x=a x=a对称
4. f ( ∣ x − a ∣ ) f(|x-a|) f(∣x−a∣)关于x=a对称
例题1:注意函数的对称性。2023年19.曲面积分就是对称性。
3.基本不等式
① 2 a b ≤ a 2 + b 2 2ab≤a^2+b^2 2ab≤a2+b2
② sin x < x < tan x , x ∈ ( 0 , π 2 ) \sin x<x<\tan x,x∈(0,\dfrac{π}{2}) sinx<x<tanx,x∈(0,2π)
③ x 1 + x < ln ( 1 + x ) < x , x ∈ ( 0 , + ∞ ) \dfrac{x}{1+x}<\ln(1+x)<x,x∈(0,+∞) 1+xx<ln(1+x)<x,x∈(0,+∞) ⇨ 1 n + 1 < ln ( 1 + 1 n ) < 1 n \dfrac{1}{n+1}<\ln(1+\dfrac{1}{n})<\dfrac{1}{n} n+11<ln(1+n1)<n1
④ 1 + x ≤ e x 1+x≤e^x 1+x≤ex
4.开根要带绝对值
a 2 = ∣ a ∣ \sqrt{a^2}=|a| a2=∣a∣
二、极限
1.考试内容概要
①极限的概念
②极限的性质
③极限存在准则
④无穷小
⑤无穷大
1.极限的概念
①数列极限
①数学语言定义(ε-N语言)

②几何意义
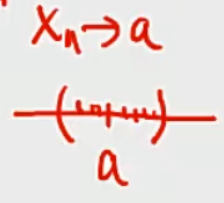
数轴,只有有限项落在区间外面,当n>N时所有点都落在开区间(a-ε,a+ε)内
i.变式
若极限为a

ii.收敛数列必有界。
单调有界 -> 收敛/有极限 -> 有界

④数列极限和部分列极限 的关系:数列极限存在且为a,则所有部分列极限也存在且为a
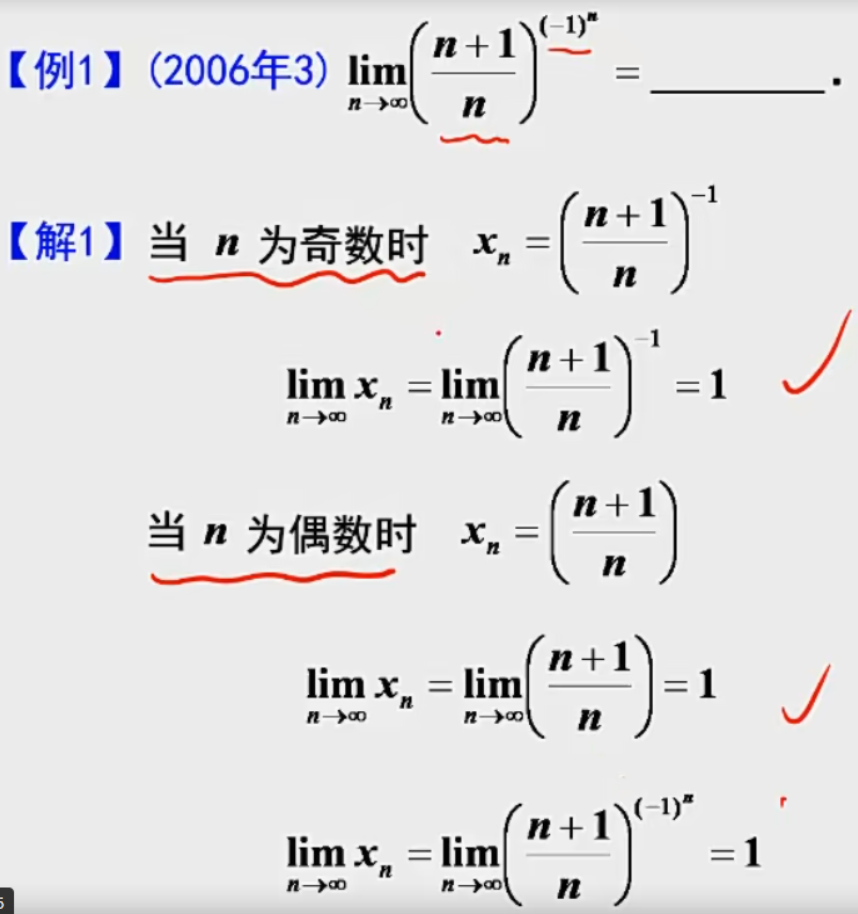
例题1:19年18. 数列极限:定积分的保号性、三角换元(有根式)、夹逼定理

答案:

例题2:08年4. 数列极限、举反例

分析:
f(x)单调 + {xn}单调 = {f(xn)}单调
f(x)单调 + f{xn}单调 = {xn}单调
对于CD,举个反例:f(x)=arctanx单调有界,{xn}=n(n=1,2,3,…),则 { f ( x n ) } = arctan n \{f(x_n)\}=\arctan n {f(xn)}=arctann,收敛于 π 2 \dfrac{π}{2} 2π,而 lim n → ∞ { x n } = lim n → ∞ n = ∞ \lim\limits_{n→∞}\{x_n\}=\lim\limits_{n→∞}n=∞ n→∞lim{xn}=n→∞limn=∞,{xn}发散
答案:B
②函数极限
函数是f(x),数列 a n = f ( n ) a_n=f(n) an=f(n),n只能取正整数。因此,函数极限是一般,数列极限的特殊。一般可以推出特殊,反之不可。
n→∞:n→+∞
x→∞:|x|→+∞
(1)自变量趋向于有限值的极限
左极限和右极限

(2)自变量趋向于无穷大的极限

定理:函数f(x)存在极限,当且仅当左右极限都存在且相等

需要区分左右极限的三种问题 (左右极限有区别,需要分)
①分段函数在分段点的极限
②
e
∞
e^∞
e∞ :分正负无穷,
e
+
∞
=
∞
,
e
−
∞
=
0
e^{+∞}=∞,e^{-∞}=0
e+∞=∞,e−∞=0
③arctan∞:分正负无穷,
a
r
c
t
a
n
+
∞
=
π
2
,
a
r
c
t
a
n
−
∞
=
−
π
2
arctan+∞=\dfrac{π}{2},arctan-∞=-\dfrac{π}{2}
arctan+∞=2π,arctan−∞=−2π
2.极限的性质
①有界性
收敛必有界
1.数列

由极限的有界性知,∃M>0,使得
∣
x
n
∣
≤
M
|x_n|≤M
∣xn∣≤M
证明:数轴上,n>N后落在a的邻域内,有界。之前的有限项,因为数量有限,所以界一定存在。综上,数列收敛,则一定有界。
2.函数

f
(
x
)
=
{
0
,
x
<
0
1
,
x
≥
0
f(x) = \begin{cases} 0, & x<0 \\ 1, & x\geq 0\end{cases}
f(x)={0,1,x<0x≥0
②保号性
如果
lim
x
→
x
0
f
(
x
)
=
A
\lim\limits_{x→x_0}f(x)=A
x→x0limf(x)=A,
(1)若
A
>
0
A>0
A>0,是 ⇨
∃
δ
>
0
\existδ>0
∃δ>0,当
0
<
∣
x
−
x
0
∣
<
δ
0<|x-x_0|<δ
0<∣x−x0∣<δ 时,
f
(
x
)
>
0
f(x)>0
f(x)>0(同理
A
<
0
A<0
A<0 时,有
f
(
x
)
<
0
f(x)<0
f(x)<0)
(2)若 ∃ δ > 0 \existδ>0 ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<δ 0<∣x−x0∣<δ 时, f ( x ) ≥ 0 f(x)≥0 f(x)≥0 ⇨ A ≥ 0 A≥0 A≥0


例题1:武忠祥老师每日一题 24.Day64 保号性、极值

分析:

答案:D
例题2:武忠祥老师每日一题 24.Day65 保号性、极值

分析:
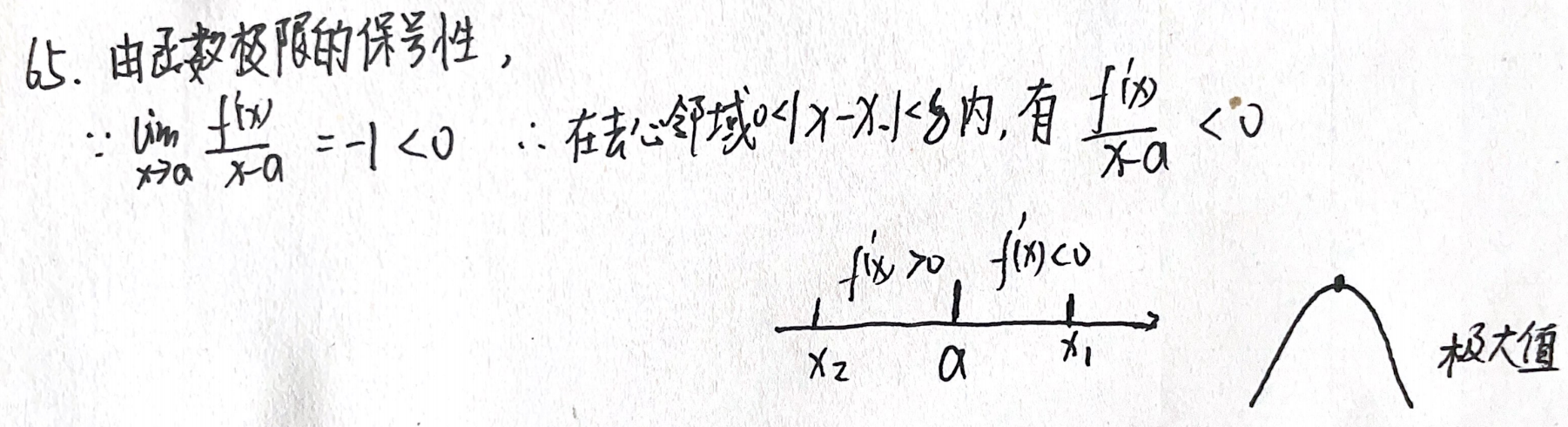
答案:B
③极限值与无穷小的关系
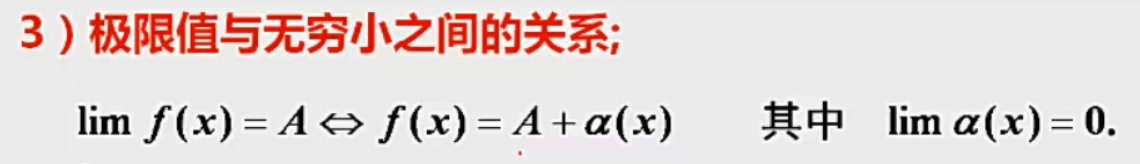
3.极限的存在准则
①单调有界准则
单调有界准则:单调有界,必有极限(数列收敛)
①单调增、有上界 ②单调减、有下界
递推关系: a n + 1 = f ( a n ) a_{n+1}=f(a_n) an+1=f(an),用单调有界准则
喻老三:考研中证明极限存在,至今为止,每次都考 单调有界准则
收敛和有极限是等价的意思。不过一般只有 数列和级数 才说收敛。
例题1:18年19. 单调有界准则证明数列极限存在
答案:

例题2:06年16.
例题3:08年4.
②夹逼定理
A<x<B,若A、B的极限都是a,则x的极限也为a
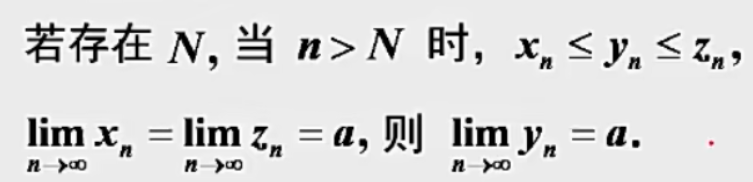
n项和:用夹逼定理
若题目中出现了形如 A<x≤B 的不等式,留意下是否可以通过变形后夹逼。
例题1:16年4. 连续的定义、可导的定义、夹逼定理
分析:从题目已知,通过变形得到题目所求的夹逼。看到有不等式,可以留意一下是否 变形后能夹逼。

答案:D
例题2:19年18.
4.无穷小量
1.无穷小量的概念
2.无穷小量的比较
3.无穷小量的性质


(1)无穷小量阶的比较
同阶无穷小 ⇦⇨ 阶数相同 ⇦⇨ 相除,趋于0时的极限=k(k为非零的任意常数)
等价无穷小 ⇦⇨ 阶数相同,系数也相同 ⇦⇨ 相除,趋于0时的极限=1
结论: ∫ 0 φ ( x ) f ( x ) d x \int_0^{φ(x)}f(x)dx ∫0φ(x)f(x)dx的阶数为 n(m+1)阶。其中φ(x)是n阶,f(x)是m阶
例题1:07年1. 等价无穷小 ⇦⇨ 阶数相同,系数也相同 ⇦⇨ 相除,趋于0时的极限=1

分析:
A.同阶,但不等价。
B:
lim
x
→
0
+
ln
1
+
x
1
−
x
x
=
lim
x
→
0
+
ln
(
1
+
x
+
x
1
−
x
)
x
=
lim
x
→
0
+
x
+
x
1
−
x
x
=
lim
x
→
0
+
1
+
x
1
−
x
=
1
\lim\limits_{x→0^+}\dfrac{\ln\dfrac{1+x}{1-\sqrt{x}}}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{\ln(1+\dfrac{x+\sqrt{x}}{1-\sqrt{x}})}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{\dfrac{x+\sqrt{x}}{1-\sqrt{x}}}{\sqrt{x}}=\lim\limits_{x→0^+}\dfrac{1+\sqrt{x}}{1-\sqrt{x}}=1
x→0+limxln1−x1+x=x→0+limxln(1+1−xx+x)=x→0+limx1−xx+x=x→0+lim1−x1+x=1
C:
1
+
x
−
1
∼
x
2
\sqrt{1+\sqrt{x}}-1\sim \dfrac{\sqrt{x}}{2}
1+x−1∼2x
D.
∼
1
2
x
\sim \dfrac{1}{2}x
∼21x
答案:B
例题2:20年1.

分析:
A:
∫
0
x
(
e
t
2
−
1
)
d
t
∼
\int_0^x(e^{t^2}-1){\rm d}t\sim
∫0x(et2−1)dt∼
∫
0
x
t
2
d
t
\int_0^xt^2{\rm d}t
∫0xt2dt,n(m+1)=1×(2+1)=3
B: ∫ 0 x l n \int_0^x\rm ln ∫0xln ( 1 + t 3 ) d t ∼ ∫ 0 x t 3 d t = ∫ 0 x t 3 2 d t (1+\sqrt{t^3}){\rm d}t\sim\int_0^x\sqrt{t^3}{\rm d}t=\int_0^xt^{\frac{3}{2}}{\rm d}t (1+t3)dt∼∫0xt3dt=∫0xt23dt,n(m+1)=1×( 3 2 {\frac{3}{2}} 23+1)= 5 2 {\frac{5}{2}} 25
C: ∫ 0 s i n x sin t 2 d t ∼ ∫ 0 s i n x t 2 d t \int_0^{sinx}\sin t^2{\rm d}t\sim \int_0^{sinx}t^2dt ∫0sinxsint2dt∼∫0sinxt2dt,n(m+1)=1×(2+1)=3
D: ∫ 0 1 − c o s x s i n 3 t d t ∼ \int_0^{1-cosx}\rm \sqrt{sin^3t}dt\sim ∫01−cosxsin3tdt∼ ∫ 0 1 2 x 2 t 3 2 d t \int_0^{\frac{1}{2}x^2}t^{\frac{3}{2}}dt ∫021x2t23dt,n(m+1)=2×( 3 2 \frac{3}{2} 23+1)=5
答案:D
例题3:

答案:
解法1:加1减1、等价无穷小替换
解法2:拉格朗日中值定理
解法3:有理化

例题4:

答案:幂指函数化eln形式,用等价无穷小代换

5.无穷大量
(1)无穷大比阶
x
x
>
>
x
!
>
>
a
x
>
>
x
a
>
>
ln
k
x
x^x>>x!>>a^x>>x^a>>\ln^kx
xx>>x!>>ax>>xa>>lnkx
幂指 >> 阶乘 >> 指数 >> 幂 >> 对数
1.无穷大量的概念:无穷大指的是 绝对值趋向于正无穷,无穷大要分正无穷大、负无穷大
2.无穷大量的比阶:幂指>阶乘>指>幂>对
3.无穷大量的性质
4.无穷大量和无界变量的关系
5.无穷大量和无穷小量的关系


一境之差,天差地别

(2)无界函数 vs 无穷大量
①无界:有一点处f(x₀)=∞
②无穷大:当x>x₀,恒有f(x)=∞
无穷大量⊇无界变量
无穷大量要求n>N后每一项都很大,要连续的无界。无界变量只要求存在有一点处无界。

例题1:唐游讲义 P30 例题14

分析:
遇到
sin
1
x
\sin\dfrac{1}{x}
sinx1,考虑
x
=
1
n
π
x=\dfrac{1}{nπ}
x=nπ1、
x
=
1
2
n
π
x=\dfrac{1}{2nπ}
x=2nπ1、
x
=
1
2
n
π
+
π
2
x=\dfrac{1}{2nπ+\dfrac{π}{2}}
x=2nπ+2π1
答案:
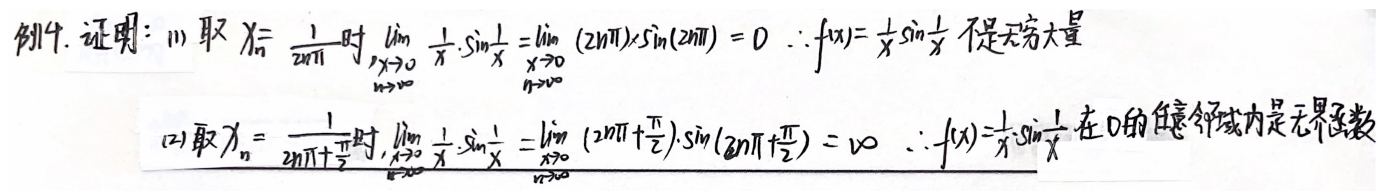
5.无穷大量与无穷小量的关系:0也是无穷小。无穷小取倒数且非0,才是无穷大。1/0无意义。


例题2:06年16. (1)证明极限存在——单调有界准则:单调有界必有极限 (2)凑重要极限,求极限

分析:
(1)证明极限存在——单调有界准则:单调有界必有极限
(2)凑重要极限,求极限

答案: e − 1 6 e^{-\frac{1}{6}} e−61

6.求极限(求极限的方法)
求极限的方法:
①等价无穷小代换 、配合 加项减项
②洛必达法则 (L’Hôpital’s rule)
③拉格朗日中值定理:出现 同一函数 在两点函数值之差
④两个重要极限、几个基本极限
⑤有界量×无穷小=无穷小
⑥泰勒公式
⑦夹逼准则
⑧导数定义
⑨定积分定义、二重积分定义

1.利用有理运算法则求极限
(2)比的极限存在,分母趋向0,则分子趋向0
(2)比的极限存在且不为0,分子趋向0,则分母趋向0 【高数辅导讲义P14】


4)若
lim
f
(
x
)
⋅
g
(
x
)
\lim f(x)·g(x)
limf(x)⋅g(x) 存在,且
lim
f
(
x
)
=
∞
\lim f(x)=∞
limf(x)=∞,则
lim
g
(
x
)
=
0
\lim g(x)=0
limg(x)=0
例题1:知道极限确定参数
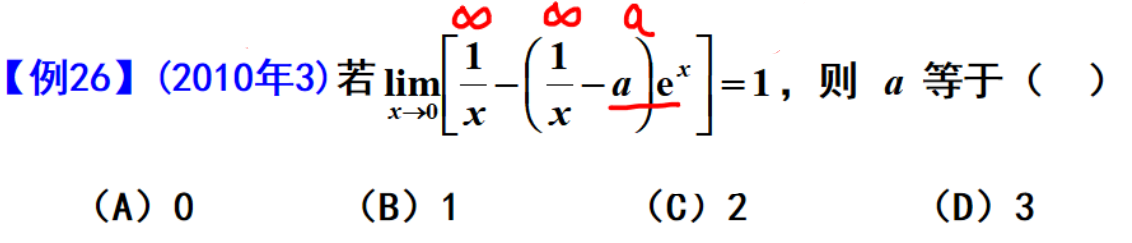
思路:把左边极限存在的一项单独拿出来,因为运算后的极限存在,所以那些不存在的项加减后极限也必然存在
答案:
例题2:
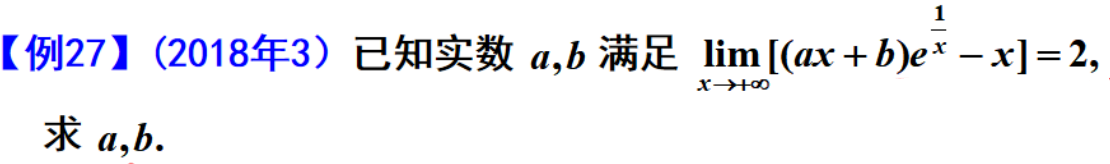
答案:
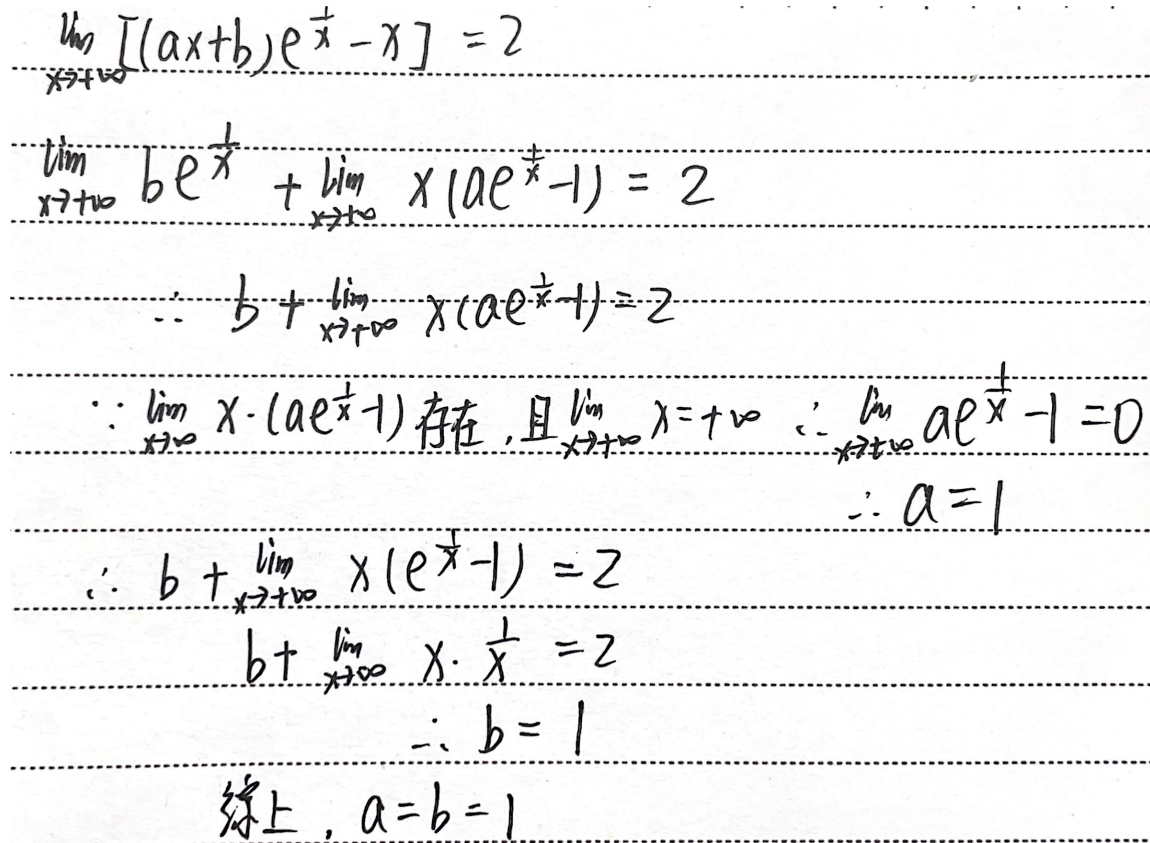
例题3:
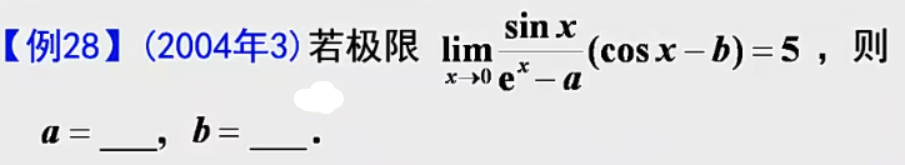
答案:有理运算法则常用结论3:极限商存在且非0,分子趋向于0,则分母也趋向于0
2.基本极限求极限 (两个重要极限)
(1)常用基本极限

lim
x
→
0
sin
x
x
=
1
lim
x
→
∞
(
1
+
1
x
)
x
=
lim
x
→
0
(
1
+
x
)
1
x
=
e
\lim\limits_{x→0}\dfrac{\sin x}{x}=1\\[2mm] \lim\limits_{x→∞}(1+\dfrac{1}{x})^x=\lim\limits_{x→0}(1+x)^\frac{1}{x}=e
x→0limxsinx=1x→∞lim(1+x1)x=x→0lim(1+x)x1=e
(2)“1∞”型极限常用结论
①凑e
②改写洛必达
③三部曲

例题1:
答案:三部曲

例题2:11年15. 重要极限

答案:
3.利用等价无穷小代换求极限
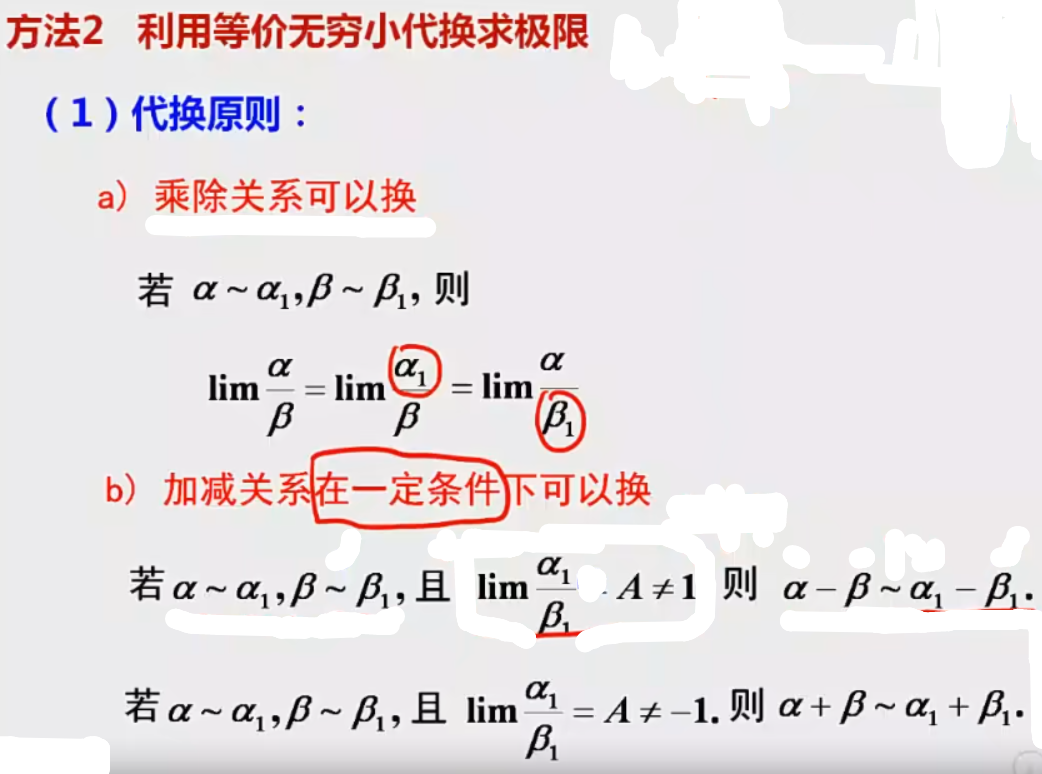
(1)代换原则:乘除关系、加减关系
①乘除关系:随便换
②加减关系:要同阶,且减法不能为1,加法不能为-1
(2)常见等价无穷小
| 阶 | 等价无穷小:x→0 |
|---|---|
| 一阶 |
x
∼
s
i
n
x
∼
t
a
n
x
∼
a
r
c
s
i
n
x
∼
a
r
c
t
a
n
x
∼
ln
(
1
+
x
)
∼
e
x
−
1
x\sim sinx\sim tanx\sim arcsinx \sim arctanx \sim \ln(1+x) \sim e^x-1
x∼sinx∼tanx∼arcsinx∼arctanx∼ln(1+x)∼ex−1 a x − 1 ∼ x ln a a^x-1 \sim x\ln a ax−1∼xlna ( 1 + x ) a − 1 ∼ a x (1+x)^a-1\sim ax (1+x)a−1∼ax, n 1 + x − 1 ∼ x n ^n\sqrt{1+x}-1 \sim \dfrac{x}{n} n1+x−1∼nx |
| 二阶 |
1
−
c
o
s
x
∼
1
2
x
2
1-cosx \sim \dfrac{1}{2}x^2
1−cosx∼21x2,
1
−
cos
α
x
∼
α
2
x
2
1-\cos^αx \sim \dfrac{α}{2}x^2
1−cosαx∼2αx2 x − ln ( 1 + x ) ∼ 1 2 x 2 x-\ln(1+x)\sim \dfrac{1}{2}x^2 x−ln(1+x)∼21x2 x→∞时: 1 x − ln ( 1 + 1 x ) ∼ 1 2 ⋅ 1 x 2 \dfrac{1}{x}-\ln(1+\dfrac{1}{x})\sim \dfrac{1}{2}·\dfrac{1}{x^2} x1−ln(1+x1)∼21⋅x21 |
| 三阶 |
x
−
sin
x
∼
1
6
x
3
x-\sin x\sim \dfrac{1}{6}x^3
x−sinx∼61x3,
tan
x
−
x
∼
1
3
x
3
\tan x-x \sim \dfrac{1}{3}x^3
tanx−x∼31x3 arcsin x − x ∼ 1 6 x 3 \arcsin x-x\sim \dfrac{1}{6}x^3 arcsinx−x∼61x3, x − arctan x ∼ 1 3 x 3 x-\arctan x \sim \dfrac{1}{3}x^3 x−arctanx∼31x3 |
| 特殊 | x→0时,
(
1
+
x
)
α
−
1
∼
α
x
(1+x)^α-1\simαx
(1+x)α−1∼αx 推广:幂指函数 α(x)→0,α(x)β(x)→0时, [ 1 + α ( x ) β ( x ) ] − 1 ∼ α ( x ) ⋅ β ( x ) [1+α(x)^{β(x)}]-1\sim α(x)·β(x) [1+α(x)β(x)]−1∼α(x)⋅β(x) |
(3)变上限积分的等价代换
若f(x)和g(x)在x=0的某邻域内连续,则 lim x → 0 f ( x ) g ( x ) = 1 \lim\limits_{x→0}\dfrac{f(x)}{g(x)}=1 x→0limg(x)f(x)=1,则 ∫ 0 x f ( t ) d t ∼ ∫ 0 x g ( t ) d t \int_0^xf(t)dt\sim \int_0^xg(t)dt ∫0xf(t)dt∼∫0xg(t)dt
推广:若 lim x → 0 φ ( x ) = 0 \lim\limits_{x→0}φ(x)=0 x→0limφ(x)=0,则有 ∫ 0 φ ( x ) f ( t ) d t ∼ ∫ 0 φ ( x ) g ( t ) d t \int_0^{φ(x)}f(t)dt\sim \int_0^{φ(x)}g(t)dt ∫0φ(x)f(t)dt∼∫0φ(x)g(t)dt
例题1:660 T7 等价无穷小
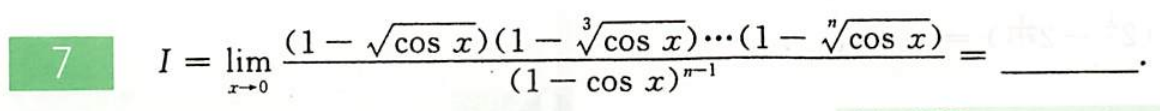
分析:等价无穷小: 1 − cos α x ∼ α ( 1 − cos x ) 1-\cos^αx\sim α(1-\cos x) 1−cosαx∼α(1−cosx)
答案: 1 n ! \dfrac{1}{n!} n!1
例题2:660 T133 经典错误
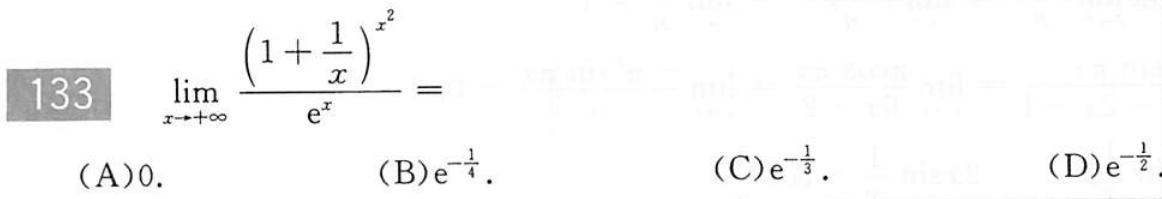
分析:
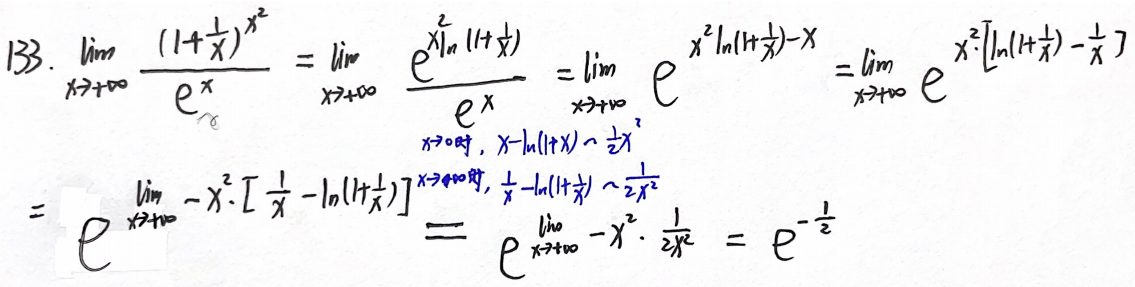
答案:D
例题3:20年9. 求极限:洛必达、泰勒公式
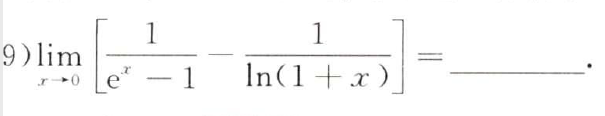
分析:
先通分:原式=
lim
x
→
0
[
l
n
(
1
+
x
)
−
(
e
x
−
1
)
(
e
x
−
1
)
[
l
n
(
1
+
x
)
]
]
=
lim
x
→
0
l
n
(
1
+
x
)
−
(
e
x
−
1
)
x
2
\lim\limits_{x→0}[\dfrac{ln(1+x)-(e^x-1)}{(e^x-1)[ln(1+x)]}]=\lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2}
x→0lim[(ex−1)[ln(1+x)]ln(1+x)−(ex−1)]=x→0limx2ln(1+x)−(ex−1)
方法1:洛必达,一直洛
方法1.5:洛必达法则+提出分子中的分式(提出
1
1
+
x
\frac{1}{1+x}
1+x1)
lim
x
→
0
l
n
(
1
+
x
)
−
(
e
x
−
1
)
x
2
=
lim
x
→
0
1
1
+
x
−
e
x
2
x
\lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2}=\lim\limits_{x→0}\dfrac{\frac{1}{1+x}-e^x}{2x}
x→0limx2ln(1+x)−(ex−1)=x→0lim2x1+x1−ex
(提出
1
1
+
x
\frac{1}{1+x}
1+x1)
=
1
2
lim
x
→
0
1
1
+
x
⋅
1
−
e
x
(
1
+
x
)
x
=
1
2
lim
x
→
0
1
−
e
x
−
x
e
x
x
=
−
1
2
lim
x
→
0
e
x
(
x
+
1
)
−
1
x
=
−
1
2
lim
x
→
0
[
e
x
(
x
+
1
)
+
e
x
]
=
−
1
2
lim
x
→
0
e
x
(
x
+
2
)
=
−
1
=\dfrac{1}{2}\lim\limits_{x→0}\dfrac{1}{1+x}·\dfrac{1-e^x(1+x)}{x}=\dfrac{1}{2}\lim\limits_{x→0}\dfrac{1-e^x-xe^x}{x}=-\dfrac{1}{2}\lim\limits_{x→0}\dfrac{e^x(x+1)-1}{x}=-\dfrac{1}{2}\lim\limits_{x→0}[e^x(x+1)+e^x]=-\dfrac{1}{2}\lim\limits_{x→0}e^x(x+2)=-1
=21x→0lim1+x1⋅x1−ex(1+x)=21x→0limx1−ex−xex=−21x→0limxex(x+1)−1=−21x→0lim[ex(x+1)+ex]=−21x→0limex(x+2)=−1
方法2:泰勒公式
l
n
(
1
+
x
)
=
x
−
x
2
2
+
o
(
x
2
)
ln(1+x)=x-\dfrac{x^2}{2}+o(x^2)
ln(1+x)=x−2x2+o(x2)
e
x
=
1
+
x
+
x
2
2
!
+
o
(
x
2
)
e^x=1+x+\dfrac{x^2}{2!}+o(x^2)
ex=1+x+2!x2+o(x2)
∴
e
x
−
1
=
x
+
x
2
2
!
+
o
(
x
2
)
∴e^x-1=x+\dfrac{x^2}{2!}+o(x^2)
∴ex−1=x+2!x2+o(x2)
lim
x
→
0
l
n
(
1
+
x
)
−
(
e
x
−
1
)
x
2
=
lim
x
→
0
[
x
−
x
2
2
+
o
(
x
2
)
]
−
[
x
+
x
2
2
!
+
o
(
x
2
)
]
x
2
=
lim
x
→
0
−
x
2
+
o
(
x
2
)
x
2
=
−
1
\lim\limits_{x→0}\dfrac{ln(1+x)-(e^x-1)}{x^2}=\lim\limits_{x→0}\dfrac{[x-\frac{x^2}{2}+o(x^2)]-[x+\frac{x^2}{2!}+o(x^2)]}{x^2}=\lim\limits_{x→0}\dfrac{-x^2+o(x^2)}{x^2}=-1
x→0limx2ln(1+x)−(ex−1)=x→0limx2[x−2x2+o(x2)]−[x+2!x2+o(x2)]=x→0limx2−x2+o(x2)=−1
答案:-1
4.利用洛必达法则求极限

① ∞ 0 ∞^0 ∞0:化为 e ln e^{\ln} eln
② ∫ 1 1 + x 2 d x = ln ( x + 1 + x 2 ) + C \int\dfrac{1}{\sqrt{1+x^2}}dx=\ln(x+\sqrt{1+x^2})+C ∫1+x21dx=ln(x+1+x2)+C
③f(x)n阶可导:最多推出n-1阶导数连续、极限存在,可用n-1次洛必达。
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)要用导数定义
f(x)n阶导数连续:n阶导数连续、极限存在,可用n次洛必达直接求出
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)
例题1:抽象函数求极限,使用洛必达法则的原则

5.利用泰勒公式求极限
泰勒展开到几次:
①加减关系:同次幂系数相加减不为0
②乘除关系:上次同次幂

例题1:

答案:①泰勒 ②洛必达+加项减项 等价无穷小
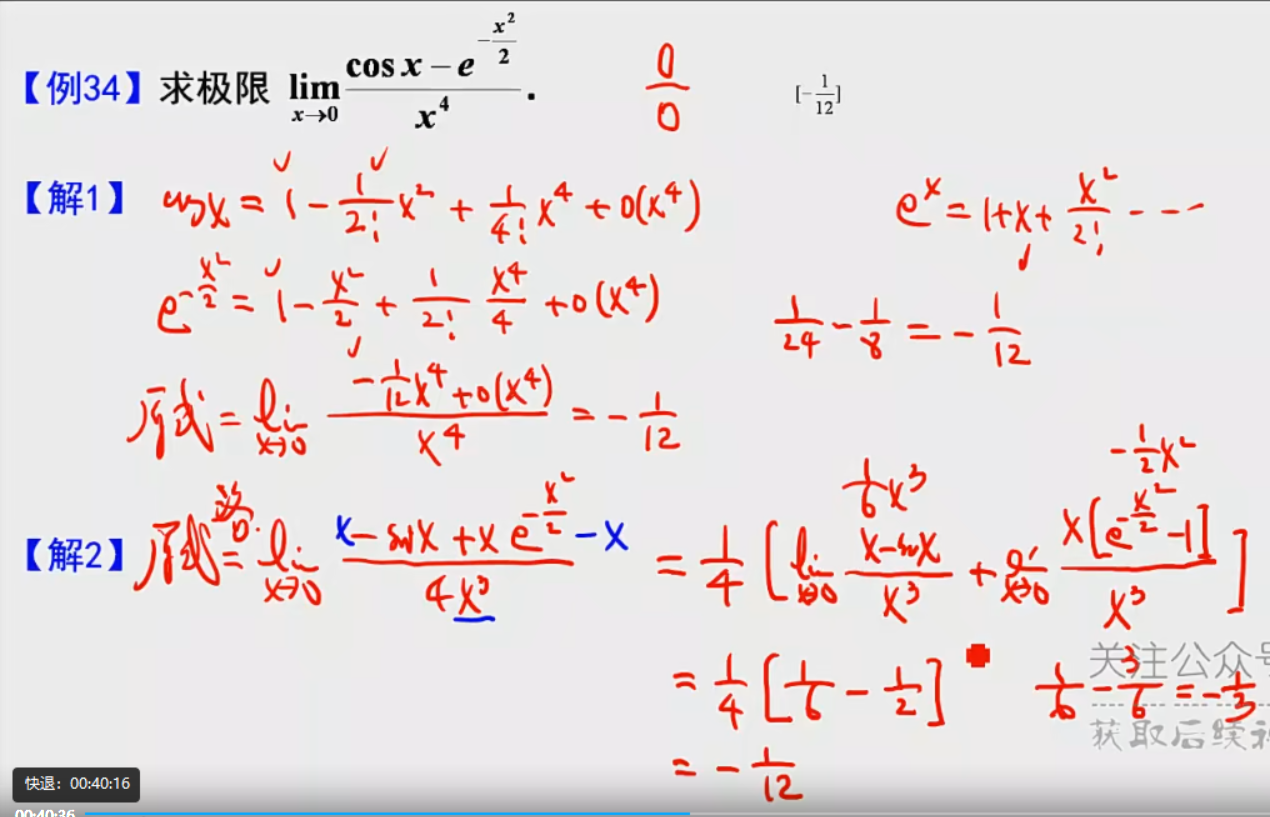
例题2:一题多解

答案:①泰勒 ②各个击破(有界量×无穷小=0) ③(选择题)代入的方法

6.利用夹逼准则求极限
lim n → ∞ \lim\limits_{n→∞} n→∞lim n a 1 n + a 2 n + . . . + a m n = m a x { a 1 , a 2 , . . . , a m } ^n\sqrt{a_1^n+a_2^n+...+a_m^n}=max\{a_1,a_2,...,a_m\} na1n+a2n+...+amn=max{a1,a2,...,am}
例题1:

答案:右边已经知道极限是3,左边大胆放缩,朝着目标是3来放缩。(有风险,万一右边求错了)

例题2:

结论:若干个数的n次方之和开根号的极限,为最大的那个数
例题2:继续用结论

例题3:几何的方法
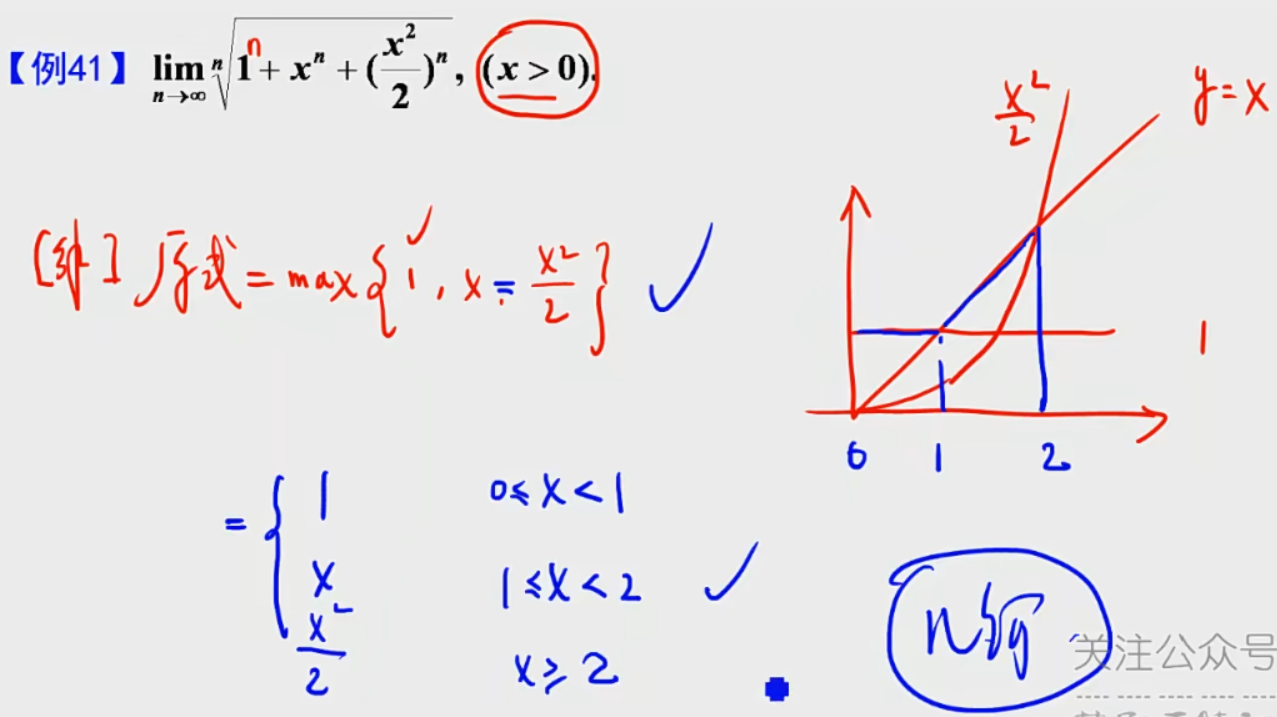
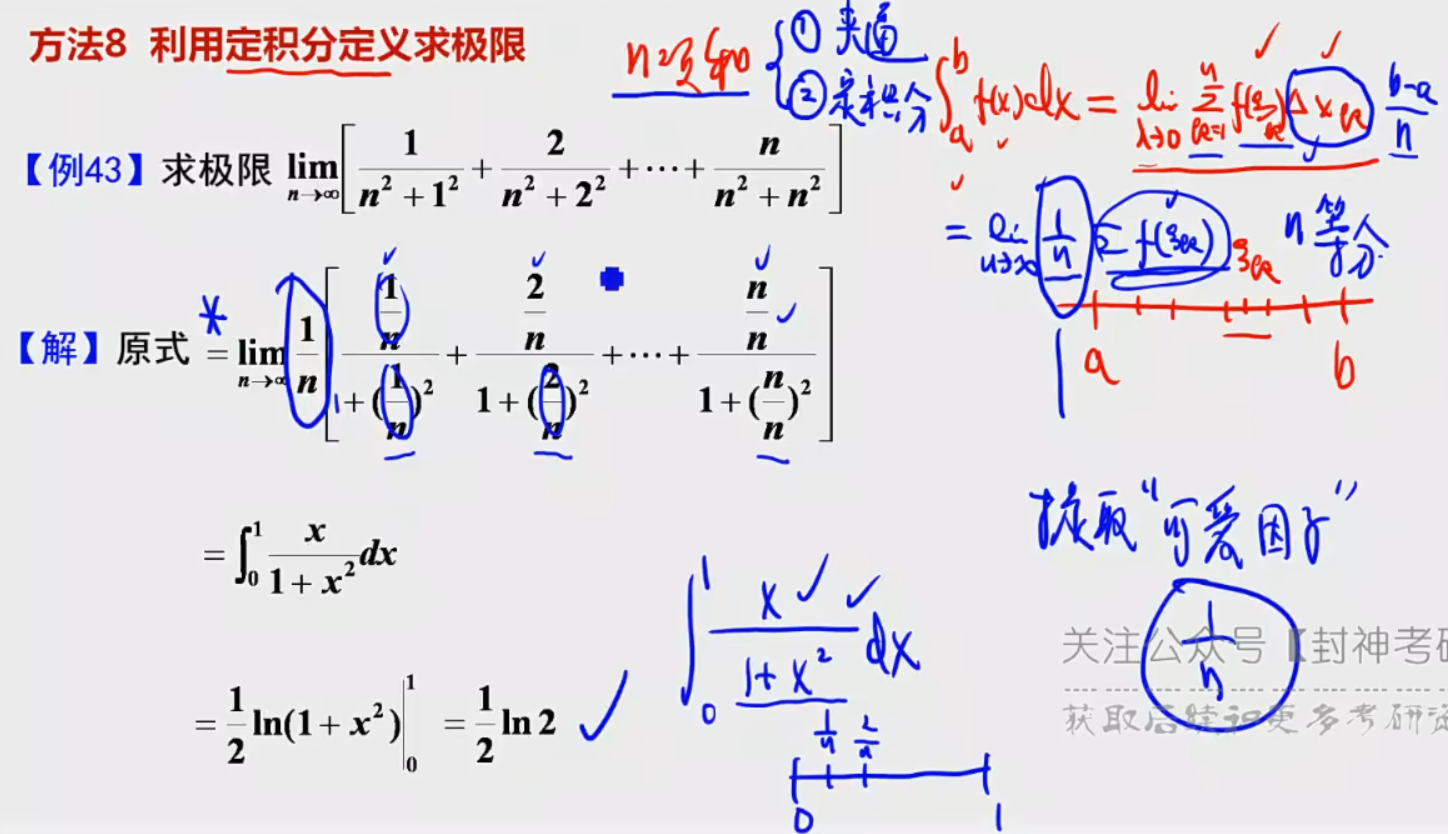
7.定积分定义求极限
提可爱因子 1 n \dfrac{1}{n} n1
判断是夹逼原理还是定积分定义:看变化部分的最大值与主体部分相比较:
①是次量级:夹逼
②是同量级:定积分定义 【高数辅导讲义 P30】
例题1:武基础班例题 定积分定义求极限
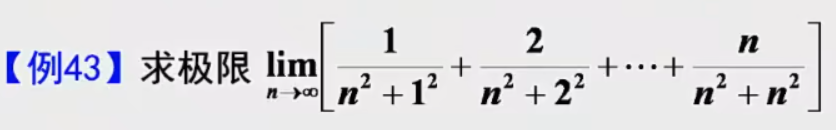
答案:
8.利用单调有界准则求极限
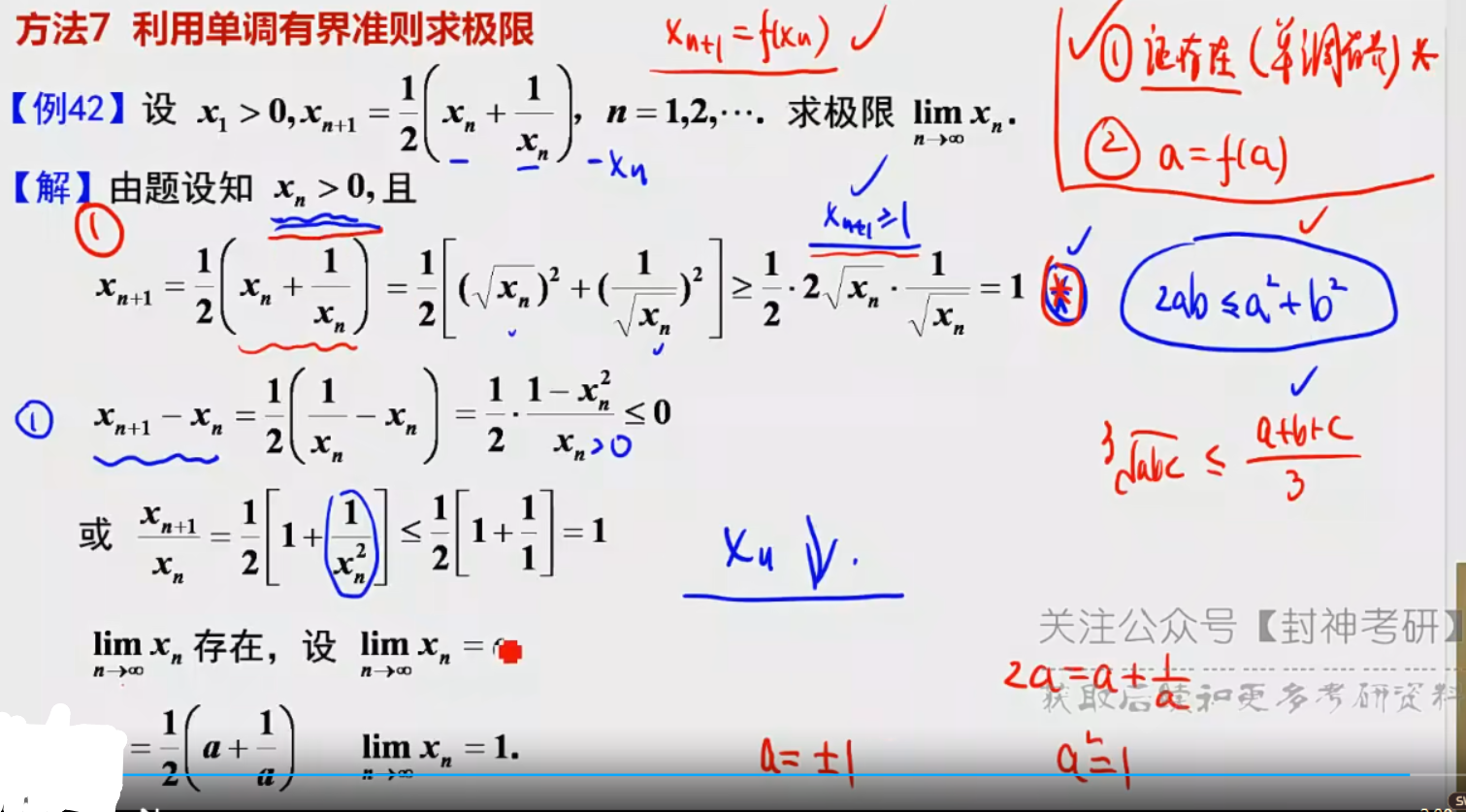
递推关系处理数列极限:
x
n
+
1
=
f
(
x
n
)
x_{n+1}=f(x_n)
xn+1=f(xn),求极限
lim
n
→
∞
x
n
\lim\limits_{n→∞}x_n
n→∞limxn:
①单调有界准则证明极限存在 ②等式两边同时取极限,求出极限
(0)基本不等式
2
a
b
≤
a
2
+
b
2
2ab≤a^2+b^2
2ab≤a2+b2
3
a
b
c
≤
a
+
b
+
c
3
^3\sqrt{abc}≤\dfrac{a+b+c}{3}
3abc≤3a+b+c
(1)证明单调性:①后项减前项 ②后项比前项(难点)
找界
求出极限
例题1:660 T19 利用单调有界准则求极限
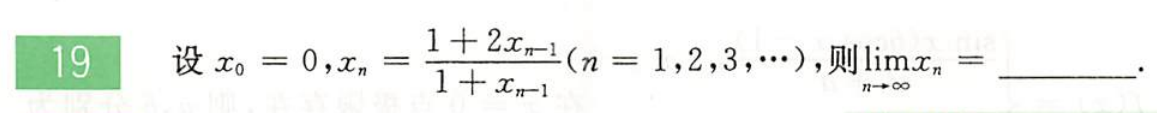
答案: 1 + 5 2 \dfrac{1+\sqrt{5}}{2} 21+5
7.求函数极限的7种未定式
7种未定式: 0 0 \dfrac{0}{0} 00、 ∞ ∞ \dfrac{∞}{∞} ∞∞、 ∞ − ∞ ∞-∞ ∞−∞、 0 ⋅ ∞ 0·∞ 0⋅∞、 1 ∞ 1^∞ 1∞、 ∞ 0 ∞^0 ∞0、 0 0 0^0 00
(1)
0
0
\dfrac{0}{0}
00
三种方法:①洛必达 ②等价无穷小 ③泰勒公式
三种化简:①极限非零因子可以先求出来 ②有理化 ③变量代换
(2)
0
⋅
∞
0·∞
0⋅∞
lim
x
→
0
+
x
ln
x
=
0
\lim\limits_{x→0^+}x\ln x=0
x→0+limxlnx=0
lim x → 0 + x a ln k x = 0 ( a > 0 , k > 0 ) \lim\limits_{x→0^+}x^a\ln^k x=0 \quad (a>0,k>0) x→0+limxalnkx=0(a>0,k>0)
(3)
∞
−
∞
∞-∞
∞−∞
①分式差:通分化为
0
0
\frac{0}{0}
00
②根式差:根式有理化
③提无穷因子 + 等价代换/换元(变量代换)/泰勒公式
(4)
1
∞
1^∞
1∞
三部曲:
①原式
=
lim
[
1
+
α
(
x
)
]
β
(
x
)
=\lim[1+α(x)]^{β(x)}
=lim[1+α(x)]β(x)
②
lim
α
(
x
)
β
(
x
)
=
A
\limα(x)β(x)=A
limα(x)β(x)=A
③原式
=
e
A
=e^A
=eA
三、连续


1.连续性的概念

2.间断点

(1)间断点的定义

(2)间断点的分类

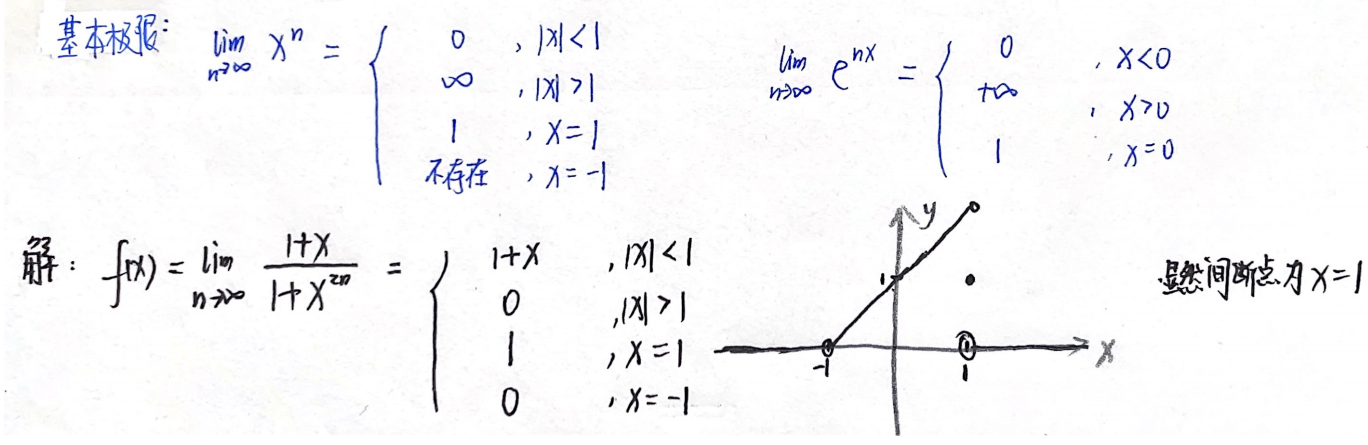
1.第一类间断点:左右极限都存在
①可去间断点:左右极限都存在,且相等
②跳跃间断点:左右极限都存在,但不等
2.第二类间断点:左右极限至少有一个不存在,为∞
①无穷间断点:存在无界点 / 瑕点,y(a)=∞,则a为无穷间断点,例如
tan
π
2
\tan \dfrac{π}{2}
tan2π
②振荡间断点:振荡不存在,但是有界,并不是无穷。典型例子sin∞:
lim
x
→
0
sin
1
x
\lim\limits_{x→0}\sin\dfrac{1}{x}
x→0limsinx1

例题1:660 T24

答案:(1,e)
例题2:

答案:①找间断点 ②求间断点处的极限,判断是第一类还是第二类间断点

例题3:

答案:

例题4:

答案:
3.连续性的运算与性质

定义区间:包含在定义域内部的区间。定义域唯一,定义区间不唯一。
例题1:

答案:

4.闭区间上连续函数的性质
1.有界性与最大最小值定理
在闭区间上连续的函数在该区间上:①有界 ②且一定能取得它的最大值与最小值
2.介值定理
设函数 f ( x ) f(x) f(x)在闭区间 [ a , b ] [a,b] [a,b]上连续,且在这区间的端点取不同的函数值 f ( a ) = A , f ( b ) = B f(a)=A,f(b)=B f(a)=A,f(b)=B,则对于A与B之间的任意一个数C,在开区间 ( a , b ) (a,b) (a,b)内至少有一点 ξ ξ ξ,使得 f ( ξ ) = C ( a < ξ < b ) f(ξ)=C \ \ (a<ξ<b) f(ξ)=C (a<ξ<b)
3.零点定理
若函数 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上连续,且 f ( a ) ⋅ f ( b ) < 0 f(a)·f(b)<0 f(a)⋅f(b)<0,则至少存在一点 ξ ∈ ( a , b ) ξ∈(a,b) ξ∈(a,b),使得 f ( ξ ) = 0 f(ξ)=0 f(ξ)=0
零点:若 x 0 x_0 x0使得 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0,那么称 x 0 x_0 x0为函数 f ( x ) f(x) f(x)的零点

例题1:

答案:最大最小值定理、介值定理

5.总结

(1)连续与可导
连续:左极限 = 函数值 =右极限
可导:左导数 = 右导数
例题1:07年4.

分析:AB是连续,CD是可导
A: lim x → 0 f ( x ) x 存在 ⇨ lim x → 0 f ( x ) = 0 → 连续 f ( 0 ) = 0 \lim\limits_{x→0}\dfrac{f(x)}{x}存在\ ⇨\ \lim\limits_{x→0}f(x)=0 \xrightarrow{连续}\ f(0)=0 x→0limxf(x)存在 ⇨ x→0limf(x)=0连续 f(0)=0
或者 lim x → 0 f ( x ) = lim x → 0 f ( x ) x ⋅ x = lim x → 0 f ( x ) x ⋅ lim x → 0 x = 0 \lim\limits_{x→0}f(x)=\lim\limits_{x→0}\dfrac{f(x)}{x}·x=\lim\limits_{x→0}\dfrac{f(x)}{x}·\lim\limits_{x→0}x=0 x→0limf(x)=x→0limxf(x)⋅x=x→0limxf(x)⋅x→0limx=0(有界×无穷小 = 无穷小)
B:两种方法同理可证 2f(0)=0
C:导数定义 lim x → 0 f ( x ) x = lim x → 0 f ( x ) − f ( 0 ) x − 0 = f ′ ( 0 ) 存在 \lim\limits_{x→0}\dfrac{f(x)}{x}=\lim\limits_{x→0}\dfrac{f(x)-f(0)}{x-0}=f'(0)存在 x→0limxf(x)=x→0limx−0f(x)−f(0)=f′(0)存在
D:举反例,|x|在x=0处不可导
答案:D
例题2:16年4.
(2) 连续与极限
若
f
(
x
n
)
f(x_n)
f(xn)连续,则
lim
n
→
∞
f
(
x
n
)
=
f
(
lim
n
→
∞
x
n
)
\lim\limits_{n→∞}f(x_n)=f(\lim\limits_{n→∞}x_n)
n→∞limf(xn)=f(n→∞limxn)
举例:
①
f
(
x
)
=
e
x
f(x)=e^x
f(x)=ex,
lim
n
→
∞
e
x
n
=
e
lim
n
→
∞
x
n
\lim\limits_{n→∞}e^{x_n}=e^{\lim\limits_{n→∞}x_n}
n→∞limexn=en→∞limxn
②
f
(
x
)
=
ln
x
f(x)=\ln x
f(x)=lnx,
lim
n
→
∞
ln
x
n
=
ln
lim
n
→
∞
x
n
\lim\limits_{n→∞}\ln{x_n}=\ln{\lim\limits_{n→∞}x_n}
n→∞limlnxn=lnn→∞limxn 【880 第一章综合填空4】
(3) 极限需要注意的问题:求极限,能否直接代入的问题
①极限非零因子可以先求出来 【辅导讲义 0/0的极限,三大化简方法】
②若剩余部分均为常数,则该处极限可以直接求 【880 第一章综合填空4】
(4) 方程根的存在性及个数
https://blog.csdn.net/Edward1027/article/details/128774498
![[网鼎杯 2020 朱雀组]Nmap 通过nmap写入木马 argcmd过滤实现逃逸](https://img-blog.csdnimg.cn/45de470718864a15ba9c255414e8ee05.png)