在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。偶然中包含着某种必然。
大数定律(law of large numbers),是一种描述当试验次数很大时所呈现的概率性质的定律。但是注意到,大数定律并不是经验规律,而是在一些附加条件上经严格证明了的定理,它是一种自然规律因而通常不叫定理而是大数“定律”。
三个重要大数定理
-
切比雪夫大数定理
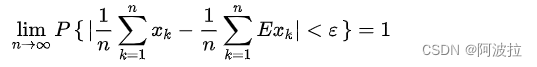
将该公式应用于抽样调查,就会有如下结论:随着样本容量n的增加,样本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计总体平均数提供了理论依据。
特别需要注意的是,切比雪夫大数定理并未要求
同分布,相较于后面介绍的伯努利大数定律和辛钦大数定律更具一般性 。
-
伯努利大数定律
设μ是n次独立试验中事件A发生的次数,且事件A在每次试验中发生的概率为p,则对任意正数ε,有公式二:
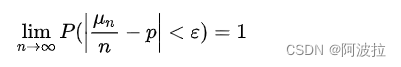
该定律是切比雪夫大数定律的特例,其含义是,当n足够大时,事件A出现的频率将几乎接近于其发生的概率,即频率的稳定性。
在抽样调查中,用样本成数去估计总体成数,其理论依据即在于此 。
-
辛钦大数定律
辛钦大数定律:常用的大数定律
对任意的ε>0,有公式三 :
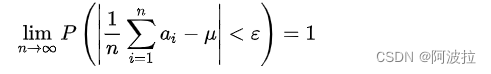











![[正确重装docker] Win10 重装 Docker 提示 Exising installation is up to date 的正确姿势](https://img-blog.csdnimg.cn/d8d50ec550f64c4eb9a916827c20fc98.png)
![P7075 [CSP-S2020] 儒略日(内附封面)](https://img-blog.csdnimg.cn/66748aef658241359714416483808a1f.png)
