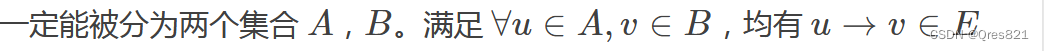时间序列数据
时间序列数据是按时间顺序以固定的时间间隔排列的观测值的集合。每个观察对应于特定的时间点，并且数据可以以各种频率（例如，每日、每月、每年）。这种类型的数据在许多领域都非常重要，包括金融，经济，气候科学等，因为它有助于通过分析时间序列数据来掌握潜在模式，发现趋势和发现季节性波动。
什么是时间序列分析？
用于评估时间序列数据以确定相关统计和其他数据属性的技术被称为时间序列分析。任何具有周期性模式的时间序列，包括金融市场、天气和社交媒体统计数据，都可能受到它的影响。时间序列分析的主要目标是研究有关市场趋势和经济周期的关键思想。
可视化在从时间序列数据中获取有见地的信息的过程中至关重要，使我们能够理解复杂的关系并做出明智的决策。
本文介绍了几种类型的图，这些图将帮助您使用Python进行时间序列分析，并使用免费访问的数据集提供了详细的示例。
数据集描述
数据集： https://github.com/jbrownlee/Datasets/blob/master/monthly-sunspots.csv
什么是太阳黑子？
太阳黑子是太阳表面的区域，被称为光球层，磁场集中，导致表面温度相对于周围环境降低。太阳复杂的磁活动是产生这些黑色区域的原因。
太阳黑子已经被观察和记录了很多年，一些最早的记录来自古代文明。了解太阳活动，空间天气及其对地球气候和通信系统的可能影响，极大地帮助了他们的研究。科学家们仍在研究太阳黑子，以更多地了解太阳磁场的动态以及它如何影响我们的太阳系。
数据集变量
该数据集由两列组成-“Month”和“Sunspots”，从1749年到1983年。它基本上描述了这个数据集中记录的每个月在太阳上看到的太阳黑子的数量。
导入必要的库
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
导入数据集
# Load the Monthly Sunspots dataset
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv"
data = pd.read_csv(url, parse_dates=['Month'], index_col='Month')
print(data)
输出
Sunspots
Month
1749-01-01 58.0
1749-02-01 62.6
1749-03-01 70.0
1749-04-01 55.7
1749-05-01 85.0
... ...
1983-08-01 71.8
1983-09-01 50.3
1983-10-01 55.8
1983-11-01 33.3
1983-12-01 33.4
[2820 rows x 1 columns]
现在，我们可以开始理解各种类型的图以及它们在Python中的实现。
1. 时间图
时间序列数据的最基本表示之一是时间图，有时称为时间序列图。x轴是时间，y轴是相关变量，它按时间顺序显示数据点。
在这项研究中使用的时间图显示了整个完整的数据集期间，从1749年到1983年的太阳黑子数量的每月波动。通过查看时间图，我们可以了解更多关于太阳黑子数据的总体趋势、季节趋势以及任何潜在的异常值或异常情况。
下面是时间图的代码示例
# Time plot
plt.figure(figsize=(7, 5))
plt.plot(data.index, data['Sunspots'], marker='o', linestyle='-', markersize=5)
plt.xlabel('Date')
plt.ylabel('Number of Sunspots')
plt.title('Monthly Sunspots Time Plot')
plt.grid(True)
plt.show()
输出
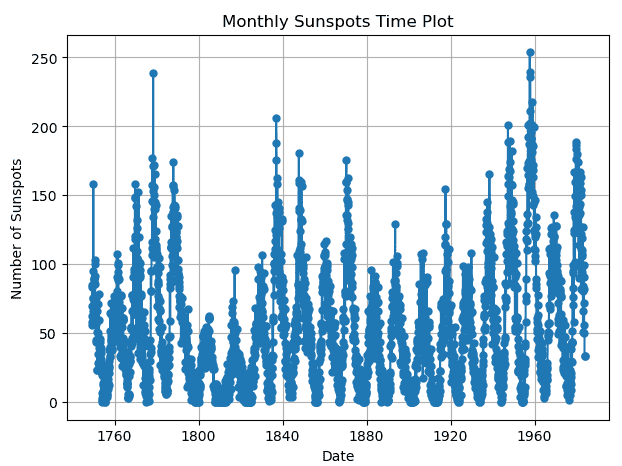
在整个数据集期间，时间图显示太阳黑子数量的月度变化。在这里，太阳黑子数量最多的时候是在1960年左右，而最少的时候是在1800年左右。
2. 线图
用直线链接数据点的简单可视化称为线图。提供时间序列数据的连续视图，强调变量随时间的趋势和变化。它主要用于跟踪数据中的长期模式。
在我们的研究中，我们采用了折线图来显示太阳黑子数量的长期趋势。这使我们能够确定太阳黑子活动的总体趋势，以及太阳黑子的数量是否随着时间的推移而上升，下降或保持不变。
让我们现在用python绘制它
# Line plot
import matplotlib.pyplot as plt
plt.figure(figsize=(7, 5))
plt.plot(data)
plt.xlabel('Date')
plt.ylabel('Number of Sunspots')
plt.title('Monthly Sunspots Line Plot')
plt.grid(True)
plt.show()
输出
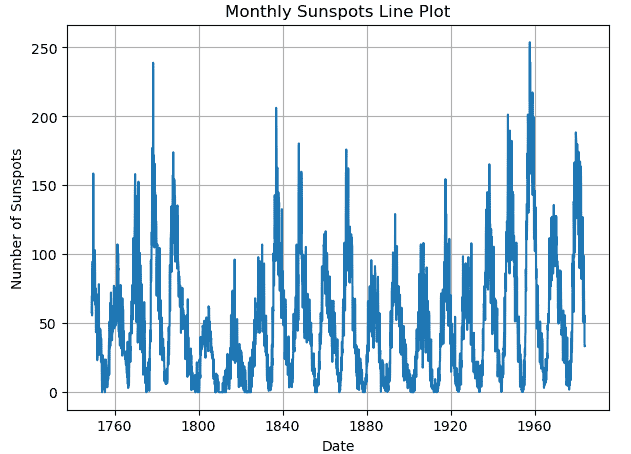
现在，时间图和线图看起来几乎相同，但重要的是要注意，线图是显示两个连续变量之间关系的图的通用术语，没有任何特定的时间重点。
另一方面，时间图是线图的一种特殊形式，它专注于可视化变量如何随时间变化，时间是x轴变量。时间图在处理时间序列数据时特别有用，其中观测按时间顺序排列并以固定的时间间隔记录。
3. 季节图
季节图将时间序列数据分解为季节分量，以说明在预定时间间隔（例如年度或月度周期）内重复出现的模式。它使我们能够识别太阳黑子活动的重复趋势，例如全年活动的变化。
下面是季节图的代码示例
# Seasonal plot
plt.figure(figsize=(7, 5))
sns.lineplot(x=data.index.month, y=data['Sunspots'], ci=None)
plt.xlabel('Month')
plt.ylabel('Number of Sunspots')
plt.title('Seasonal Plot')
plt.xticks(range(1, 13), labels=[
'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
plt.grid(True)
plt.show()
输出
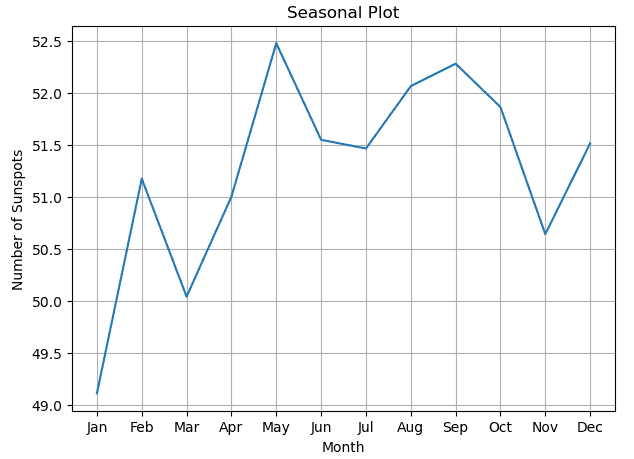
从这个季节图中，我们可以了解更多关于太阳活动的季节性，它揭示了太阳黑子活动倾向于较高或较低的月份。
4. 直方图和密度图
密度图被定义为用于可视化数据分布并估计连续随机变量的概率密度函数（PDF）的图形表示。它基本上是直方图的平滑版本，提供表示底层数据分布的连续曲线。当处理大型数据集或需要平滑、连续的数据表示来揭示值在整个时间序列中的分布时，这些图是合适的。
下面是直方图和密度图的代码示例
# Histogram and Density Plot
plt.figure(figsize=(7, 5))
sns.histplot(data['Sunspots'], kde=True)
plt.xlabel('Number of Sunspots')
plt.ylabel('Frequency')
plt.title('Histogram and Density Plot')
plt.grid(True)
plt.show()
输出
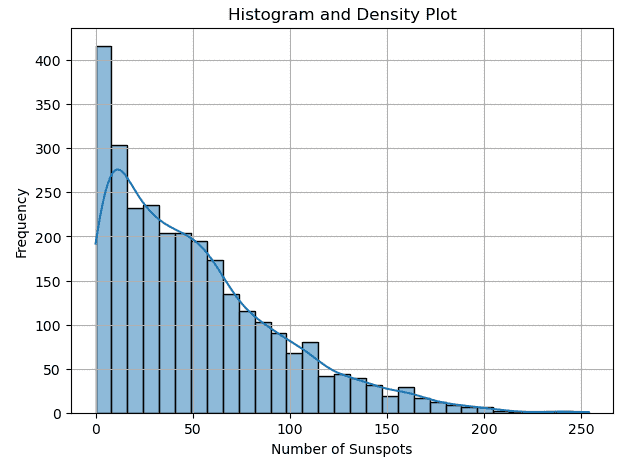
密度图和直方图显示了太阳黑子数量的频率分布，这有助于我们理解太阳黑子分布的形式及其集中趋势。
5. 自相关图
自相关图，也称为相关图，是一种时间序列分析工具，用于显示时间序列在不同滞后下与自身的自相关性。通过自相关来测量数据点与其在各种时间滞后处的先前观测值之间的联系。它基本上表示时间序列与其自身滞后值之间的相关性。图主要用于识别数据中的季节滞后。
现在让我们使用Python绘制一个自相关图
# Autocorrelation Plot
plt.figure(figsize=(7,5))
plot_acf(data['Sunspots'], lags=50)
plt.xlabel('Lags')
plt.ylabel('Autocorrelation')
plt.title('Autocorrelation Plot')
plt.grid(True)
plt.show()
输出
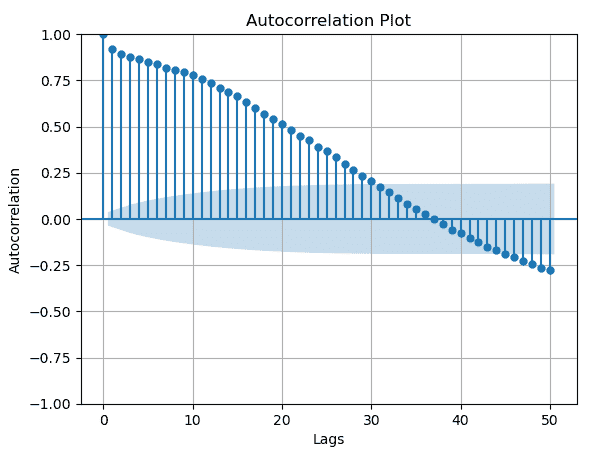
自相关图显示了不同滞后的相关性，这对于理解太阳黑子活动的季节性模式很有用。一个重大的自相关在特定的延迟表明，太阳黑子活动可能遵循每年的模式。
6. 偏自相关函数（PACF）图
偏自相关函数（PACF）图是时间序列分析中用于确定时间序列的自回归（AR）阶的图形工具。在考虑所有中间延迟的影响的同时，它显示了每个延迟对时间序列的当前值的直接影响。基本上，它检查数据点与其先前观测值之间的相关性，而不考虑干预时间步长的影响。
以下是偏自相关函数（PACF）图的代码示例
# PACF plot
plt.figure(figsize=(7, 5))
plot_pacf(data['Sunspots'], lags=50)
plt.xlabel('Lags')
plt.ylabel('Partial Autocorrelation')
plt.title('Partial Autocorrelation Function (PACF) Plot')
plt.grid(True)
plt.show()
输出
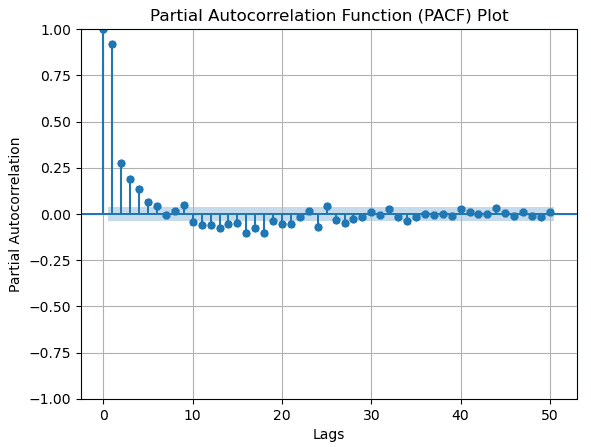
在我们的方法中，滞后观测的数量与当前的太阳黑子计数的实质性影响确定使用的PACF图。PACF帮助选择AR模型对太阳黑子活动的预测顺序。
7. 极坐标图
极坐标图是数据可视化图，其中数据点以圆形图案布置。围绕圆的角度和距中心的径向距离用于表示各种变量或数据属性。这些主要用于可视化数据集中的季节模式。
下面是极坐标图的代码示例
# Extracting the month and year from the index of the above dataset "Monthly Sunspots"
data['Month_Num'] = data.index.month
# Grouping the data by month, calculating the average number of sunspots for each month
monthly_average = data.groupby('Month_Num')['Sunspots'].mean()
# Polar Plot theta (angle) and radii (length) settings
theta = np.linspace(0, 2 * np.pi, len(monthly_average))
radii = monthly_average.values
# Polar Plot
plt.figure(figsize=(7, 5))
plt.polar(theta, radii)
plt.title('Polar Plot of Monthly Average Sunspots')
plt.xticks(theta, ['Jan', 'Feb', 'Mar', 'Apr', 'May',
'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
# Set y-axis limit to accommodate the data
plt.ylim(0, radii.max() + 10)
plt.show()
输出
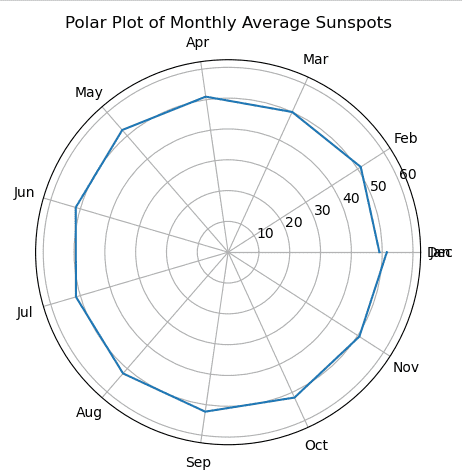
在这种特殊情况下，极坐标图显示了每个月太阳黑子的平均数量。距中心的径向距离反映了每个月的太阳黑子的平均数量，而圆内的角位置表示每个月（例如，一月、二月、三月等）。它揭示了数据中存在的任何季节性趋势，并使我们能够看到太阳黑子活动年度周期中的周期性模式。
月平均太阳黑子视图在极坐标图中显示得非常迷人，它还揭示了全年的周期性趋势。
8. 移动平均图
在时间序列分析中，移动平均图是一种流行的数据可视化方法，用于发现数据中的趋势和模式。其主要目标是通过确定连续数据点的特定窗口的平均值来消除短期波动并揭示数据的长期趋势。
对窗口内的数据点进行平均，并将所得值显示在图表上以生成移动平均值图。当移动平均线位于原始数据图上时，更容易发现和比较趋势和季节性模式。
下面是移动平均线图的代码示例
# Moving Average Plot
plt.figure(figsize=(7, 5))
values = data['Sunspots']
# 7-day moving average
rolling_mean = values.rolling(window=7).mean()
plt.plot(values, label='Original')
plt.plot(rolling_mean, label='7-day Moving Average', color='red')
plt.xlabel('Date')
plt.ylabel('Value')
plt.title('Moving Average Plot')
plt.legend()
plt.grid(True)
plt.show()
输出
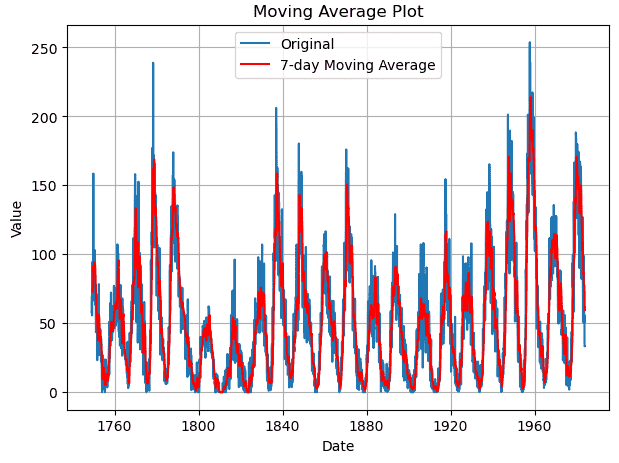
我们在这里绘制了一个7天移动平均线。我们知道，移动平均是一种通过确定后续数据点的预定窗口的平均值来平滑数据的技术。用于求平均的数据点的数量取决于窗口大小，通常称为移动平均周期。这种方法涉及在七天的时间内平均初始太阳黑子数据。
总结
通过利用这些各种图表和数据可视化技术，我们可以全面了解“每月太阳黑子”数据集，识别模式，并提取有关几个世纪以来太阳活动的宝贵见解。
作为这项研究的结果，您现在拥有将这些技术应用于各种部门和行业的时间序列数据集所需的知识。时间序列分析提供了重要的工具，可以在任何需要序列数据的领域（包括经济学，金融，气候研究和其他领域）获得有见地的见解并做出数据驱动的决策。通过采用这些方法，我们有能力利用时间相关的数据，并利用其预测潜力来解决现实世界的问题。
![[MAUI]实现动态拖拽排序网格](https://img-blog.csdnimg.cn/03ff870c203b4b96ac9d1cfadbb3ce41.gif)
