文章目录

双周赛113
- [2855. 使数组成为递增数组的最少右移次数](https://leetcode.cn/problems/minimum-right-shifts-to-sort-the-array/)
- - 暴力枚举
  - 贪心 O(n)
- [2856. 删除数对后的最小数组长度](https://leetcode.cn/problems/minimum-array-length-after-pair-removals/)
- - 分类讨论
  - 二分查找 O(logn)
- [2857. 统计距离为 k 的点对](https://leetcode.cn/problems/count-pairs-of-points-with-distance-k/)
- - 枚举值域 ==> 两数之和
- [2858. 可以到达每一个节点的最少边反转次数](https://leetcode.cn/problems/minimum-edge-reversals-so-every-node-is-reachable/)
- - 换根DP

双周赛113

2855. 使数组成为递增数组的最少右移次数

简单

给你一个长度为 n 下标从 0 开始的数组 nums ，数组中的元素为 互不相同 的正整数。请你返回让 nums 成为递增数组的 最少右移 次数，如果无法得到递增数组，返回 -1 。

一次右移指的是同时对所有下标进行操作，将下标为 i 的元素移动到下标 (i + 1) % n 处。

示例 1：

输入：nums = [3,4,5,1,2]
输出：2
解释：
第一次右移后，nums = [2,3,4,5,1] 。
第二次右移后，nums = [1,2,3,4,5] 。
现在 nums 是递增数组了，所以答案为 2 。

示例 2：

输入：nums = [1,3,5]
输出：0
解释：nums 已经是递增数组了，所以答案为 0 。

示例 3：

输入：nums = [2,1,4]
输出：-1
解释：无法将数组变为递增数组。

提示：

1 <= nums.length <= 100
1 <= nums[i] <= 100
nums 中的整数互不相同。

暴力枚举

至多移动n-1次，枚举以每个下标为第一位元素，然后查看是否为递增数组

贪心 O(n)

使数组成为递增数组，那么最小值一定在最左边，找到最小值，然后检查一遍右侧元素是否都小于当前元素

class Solution {
    public int minimumRightShifts(List<Integer> nums) {
        int mnidx = -1, mn = Integer.MAX_VALUE;
        for(int i = 0; i < nums.size(); i++){
            if(nums.get(i) < mn){
                mn = nums.get(i);
                mnidx = i;
            }
        }
        int j = mnidx;
        for(int i = 0; i < nums.size()-1; i++){
            int suf = nums.get((j+1)% nums.size());
            if(suf < nums.get(j)) return -1;
            j = (j + 1) % nums.size();
        }
        return (nums.size() - mnidx) % nums.size();
    }
}

2856. 删除数对后的最小数组长度

中等

给你一个下标从 0 开始的 非递减 整数数组 nums 。

你可以执行以下操作任意次：

选择两个下标 i 和 j ，满足 i < j 且 nums[i] < nums[j] 。
将 nums 中下标在 i 和 j 处的元素删除。剩余元素按照原来的顺序组成新的数组，下标也重新从 0 开始编号。

请你返回一个整数，表示执行以上操作任意次后（可以执行 0 次），nums 数组的最小数组长度。

示例 1：

输入：nums = [1,3,4,9]
输出：0
解释：一开始，nums = [1, 3, 4, 9] 。
第一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 1 < 3 。
删除下标 0 和 1 处的元素，nums 变成 [4, 9] 。
下一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 4 < 9 。
删除下标 0 和 1 处的元素，nums 变成空数组 [] 。
所以，可以得到的最小数组长度为 0 。

示例 2：

输入：nums = [2,3,6,9]
输出：0
解释：一开始，nums = [2, 3, 6, 9] 。
第一次操作，我们选择下标 0 和 2 ，满足 nums[0] < nums[2] <=> 2 < 6 。
删除下标 0 和 2 处的元素，nums 变成 [3, 9] 。
下一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 3 < 9 。
删除下标 0 和 1 处的元素，nums 变成空数组 [] 。
所以，可以得到的最小数组长度为 0 。

示例 3：

输入：nums = [1,1,2]
输出：1
解释：一开始，nums = [1, 1, 2] 。
第一次操作，我们选择下标 0 和 2 ，满足 nums[0] < nums[2] <=> 1 < 2 。
删除下标 0 和 2 处的元素，nums 变成 [1] 。
无法对数组再执行操作。
所以，可以得到的最小数组长度为 1 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 109
nums 是 非递减 数组。

分类讨论

https://leetcode.cn/problems/minimum-array-length-after-pair-removals/solutions/2446146/olog-n-tan-xin-er-fen-cha-zhao-pythonjav-t3qn/

class Solution {
    /**
    设元素 x 的出现次数为 cx

    从特例入手，分类讨论：
    1. 当 cx > n/2：2*cx-n
        没法全部抵消: 2*cx-n
            众数 x 出现 cx 次，其他数出现 n-cx 次
            那么 可以抵消 2*(n-cx) 个，剩余元素数量为 n - 2*(n-cx) 个
            花间 2cx - n
    
    2. 当 cx <= n/2: 
        可以几乎全部抵消
            n 是偶数，剩余 0 个数
            n 是奇数，剩余 1 个数
     */
    public int minLengthAfterRemovals(List<Integer> nums) {
        int n = nums.size();
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums){
            map.merge(num, 1, Integer::sum);
        }
        int cx = -1;
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
            if(entry.getValue() > cx)
                cx = entry.getValue();
        }
        if(cx > n / 2) return 2*cx - n;
        else return n % 2;
        
    }
}

二分查找 O(logn)

class Solution {
    /**
    由于数组是有序的，如果maxcnt超过数组的一半，那么nums[n/2]一定是出现次数最多的那个数
    然后用二分查找计算出nums[n/2]第一次和最后一次出现的位置，从而算出maxcnt
    
     */
    public int minLengthAfterRemovals(List<Integer> nums) {
        int n = nums.size();
        int x = nums.get(n / 2);
        int left = lowerBound(nums, x);
        int right = lowerBound(nums, x+1); // upperBound(nums, x);
        // x个数：[left, right)
        return Math.max((right - left) * 2 - n, n % 2);
    }

    // upper_bound ： 返回第一个大于key的元素下标
    public int upperBound(List<Integer> list, int target){
        int left = 0, right = list.size();
        while(left < right){
            int mid = (left + right) >> 1;
            if(list.get(mid) > target) right = mid;
            else left = mid + 1;
        }
        return left;
    }
    // lower_bound ： 返回第一个大于或等于key的元素下标
    public int lowerBound(List<Integer> list, int target){
        int left = 0, right = list.size();
        while(left < right){
            int mid = (left + right) >> 1;
            if(list.get(mid) < target) left = mid + 1;
            else right = mid;
        }
        return left;
    }
}

2857. 统计距离为 k 的点对

中等

给你一个二维整数数组 coordinates 和一个整数 k ，其中 coordinates[i] = [xi, yi] 是第 i 个点在二维平面里的坐标。

我们定义两个点 (x1, y1) 和 (x2, y2) 的距离为 (x1 XOR x2) + (y1 XOR y2) ，XOR 指的是按位异或运算。

请你返回满足 i < j 且点 i 和点 j之间距离为 k 的点对数目。

示例 1：

输入：coordinates = [[1,2],[4,2],[1,3],[5,2]], k = 5
输出：2
解释：以下点对距离为 k ：
- (0, 1)：(1 XOR 4) + (2 XOR 2) = 5 。
- (2, 3)：(1 XOR 5) + (3 XOR 2) = 5 。

示例 2：

输入：coordinates = [[1,3],[1,3],[1,3],[1,3],[1,3]], k = 0
输出：10
解释：任何两个点之间的距离都为 0 ，所以总共有 10 组点对。

提示：

2 <= coordinates.length <= 50000
0 <= xi, yi <= 106
0 <= k <= 100

枚举值域 ==> 两数之和

https://leetcode.cn/problems/count-pairs-of-points-with-distance-k/solutions/2445629/bao-li-zhu-yi-k-de-fan-wei-by-endlessche-3i1b/

class Solution {
    // 点 i 和点 j之间距离为 k
    // (x1 XOR x2) + (y1 XOR y2) = k
    // 由于 0 <= x1 XOR x2 <= i
    //      0 <= y1 XOR y2 <= k-i
    // 枚举 (x2, y2) => (x1 ^ i, y1 ^ (k-i))
    // 两数之和
    public int countPairs(List<List<Integer>> coordinates, int k) {
        Map<String, Integer> map = new HashMap<>();
        int cnt = 0;
        for(List<Integer> coordinate : coordinates){
            int x = coordinate.get(0), y = coordinate.get(1);
            for(int i = 0; i <= k; i++){
                String key = (x ^ i) + "_" + (y ^ (k-i));
                cnt += map.getOrDefault(key, 0);
            }
            map.merge(x + "_" + y, 1, Integer::sum);
        }
        return cnt;
    }
}

2858. 可以到达每一个节点的最少边反转次数

困难

给你一个 n 个点的 简单有向图 （没有重复边的有向图），节点编号为 0 到 n - 1 。如果这些边是双向边，那么这个图形成一棵树。

给你一个整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条 有向边 。

边反转 指的是将一条边的方向反转，也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。

对于范围 [0, n - 1] 中的每一个节点 i ，你的任务是分别独立计算最少需要多少次 边反转 ，从节点 i 出发经过 一系列有向边 ，可以到达所有的节点。

请你返回一个长度为 n 的整数数组 answer ，其中 answer[i]表示从节点 i 出发，可以到达所有节点的 最少边反转 次数。

示例 1：

输入：n = 4, edges = [[2,0],[2,1],[1,3]]
输出：[1,1,0,2]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 1 。
对于节点 1 ：反转 [2,1] ，从节点 1 出发可以到达所有节点。
所以 answer[1] = 1 。
对于节点 2 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[2] = 0 。
对于节点 3 ：反转 [1,3] 和 [2,1] ，从节点 3 出发可以到达所有节点。
所以 answer[3] = 2 。

示例 2：

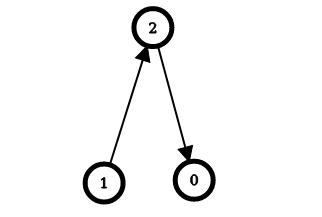
输入：n = 3, edges = [[1,2],[2,0]]
输出：[2,0,1]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] 和 [1,2] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 2 。
对于节点 1 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[1] = 0 。
对于节点 2 ：反转 [1,2] ，从节点 2 出发可以到达所有节点。
所以 answer[2] = 1 。

提示：

2 <= n <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ui == edges[i][0] < n
0 <= vi == edges[i][1] < n
ui != vi
输入保证如果边是双向边，可以得到一棵树。

换根DP

https://leetcode.cn/problems/minimum-edge-reversals-so-every-node-is-reachable/solutions/2445681/mo-ban-huan-gen-dppythonjavacgojs-by-end-8qiu/

class Solution {
    private List<int[]>[] g;
    private int[] ans, size;


    public int[] minEdgeReversals(int n, int[][] edges) {
        g = new ArrayList[n]; // g[x] 表示 x 的所有邻居
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(new int[]{y, 1});
            g[y].add(new int[]{x, -1}); // 有向图，标记y到x为反向
        }
        ans = new int[n];
        dfs(0, -1); // 计算ans[0]
        reroot(0, -1); // 0 没有父节点 
        return ans;
    }

    private void dfs(int x, int fa){
        for(int[] e : g[x]){ // 遍历 x 的邻居 y
            int y = e[0], dir = e[1];
            if(y != fa){ // 避免访问父节点
                if(dir < 0) 
                    ans[0] += 1;
                dfs(y, x); // x 是 y 的父节点
            }
        }
    }

    private void reroot(int x, int fa){
        for(int[] e : g[x]){ // 遍历 x 的邻居 y
            int y = e[0], dir = e[1];
            if(y != fa){ // 避免访问父节点
            	// 这里是变化点，按照题目要求更改
                ans[y] = ans[x] + dir; // dir 就是 从 x 换到 y 的 变化量
                reroot(y, x); // x 是 y 的父节点
            }
        }
    }

}