https://atcoder.jp/contests/arc163/tasks/arc163_d

首先竞赛图有个性质：

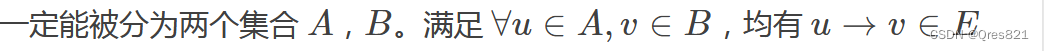
然后有了这个性质，我们就可以考虑计数题的经典套路，拆贡献算总和。

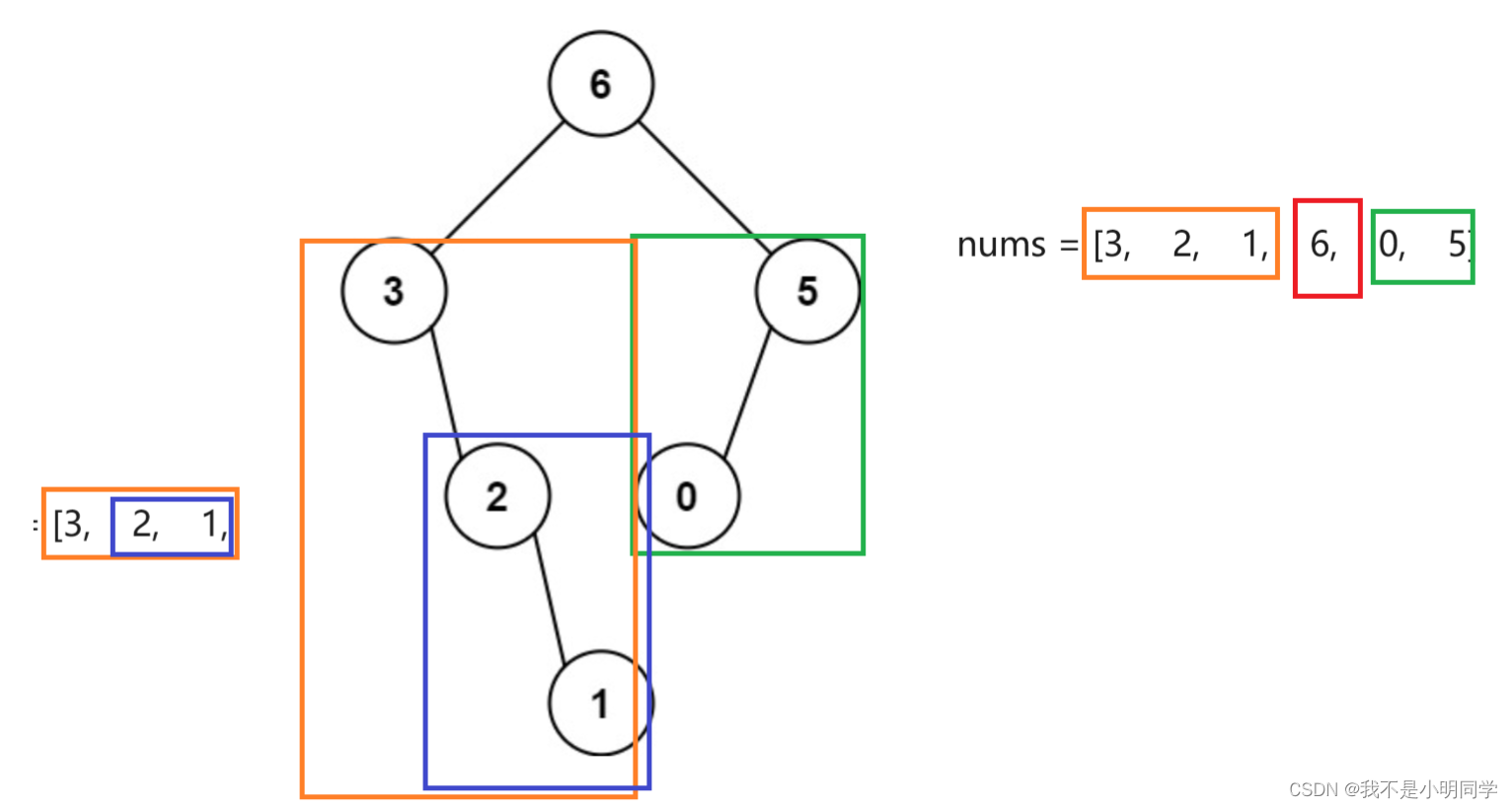
考虑假如我们成功划分成两个集合 $A,B$，其中一个可以为空（我们可以令 $A$ 可以为空，防止算重），我们就记为算到一个新的连通块。

为什么是对的？

考虑对于 $k$ 个连通块的竞赛图，必然会有 $k$ 种划分方法。而对应每种划分方法，恰好也对应着其某些竞赛图的一种划分方式中相对应的连通分量。这个过程形成一个双射关系。

最关键的地方抓住了，然后剩下直接上dp就行了。

$d{p}_{i,j,k}$ 前 $i$ 个点，$j$ 个在 $A$ 里，有 $k$ 个为小连大。转移枚举在哪个连通块，有多少条边为小连大，转移系数乘个组合数就行了。

	f[1][0][0]=f[1][1][0]=1; 
	for(i=1; i<n; ++i) {
		for(j=0; j<=i; ++j) 
			for(k=0; k<=m; ++k) {
				for(c=0; c<=j && k+c<=m; ++c) {
					Add(f[i+1][j+1][k+c], f[i][j][k]*C(j, c)%mo); 
				}
				for(c=0; c<=i-j && k+j+c<=m; ++c) {
					Add(f[i+1][j][k+j+c], f[i][j][k]*C(i-j, c)%mo); 
				}
			}
	}
	for(i=0; i<n; ++i) Add(ans, f[n][i][m]);