LeetCode - The World's Leading Online Programming Learning Platform

题目大意 

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

解题思路 

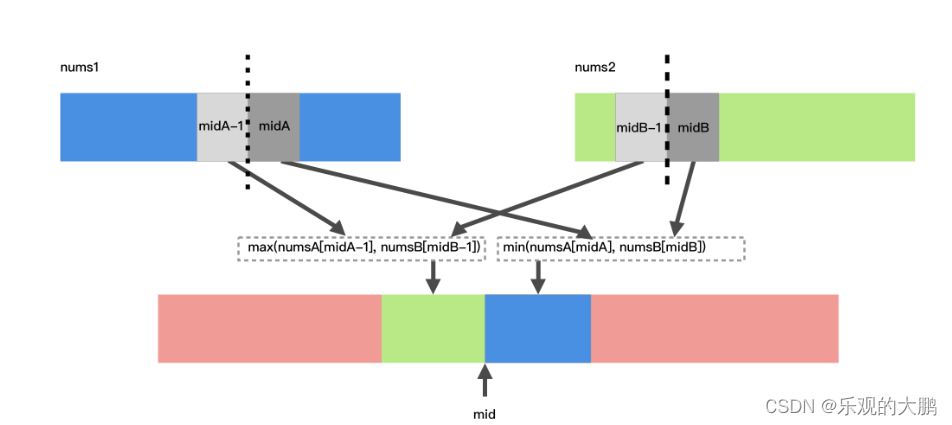
一、最容易想到的办法是把两个数组合并，然后取出中位数。但是合并有序数组的操作是 O(m+n) 的，不符合题意。看到题目给的 log 的时间复杂度，很容易联想到二分搜索。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
            int size = nums1.length + nums2.length;
            int index1 = 0;
            int index2 = 0;
            int end = size/2;
            int begin = end;
            if (size % 2 == 0) {
                begin = begin-1;
            }
            int [] result = new int[end];

            int index = 0;
            while (index1 + index2 < size && index <= end) {
                if (index1 > nums1.length - 1) {
                    result[index++] = nums2[index2++];
                    continue;
                }
                if (index2 > nums2.length - 1) {
                    result[index++] = nums1[index1++];
                    continue;
                }
                if (nums1[index1] <= nums2[index2]) {
                    result[index++] = nums1[index1++];
                    continue;
                }
                result[index++] = nums2[index2++];
            }
            return (result[begin] + result[end])/2d;
    }
}

二、去中位进行两个数组移动