1.回顾插入操作
- ·插入新结点后,要保持二叉排序树的特性不变(左<中<右)
- 若插入新结点导致不平衡,则需要调整平衡。
2.删除操作
- 删除结点后,要保持二叉排序树的特性不变(左<中<右)
- 若删除结点导致不平衡,则需要调整平衡。
1.具体步骤:
1 . 用二叉排序树的方法删除结点:详情见:二叉排序树删除规则
- 若删除的结点是叶子,直接删。
- 若删除的结点只有一个子树,用子树顶替删除位置。
- 若删除的结点有两棵子树,用前驱(或后继)结点。
- 顶替,并转换为对前驱(或后继)结点的删除。
2 . 从叶子结点一路向上找“最小不平衡子树”
3 . 若找到了最小平衡二叉树,找到高度最大的儿子结点和孙子结点。
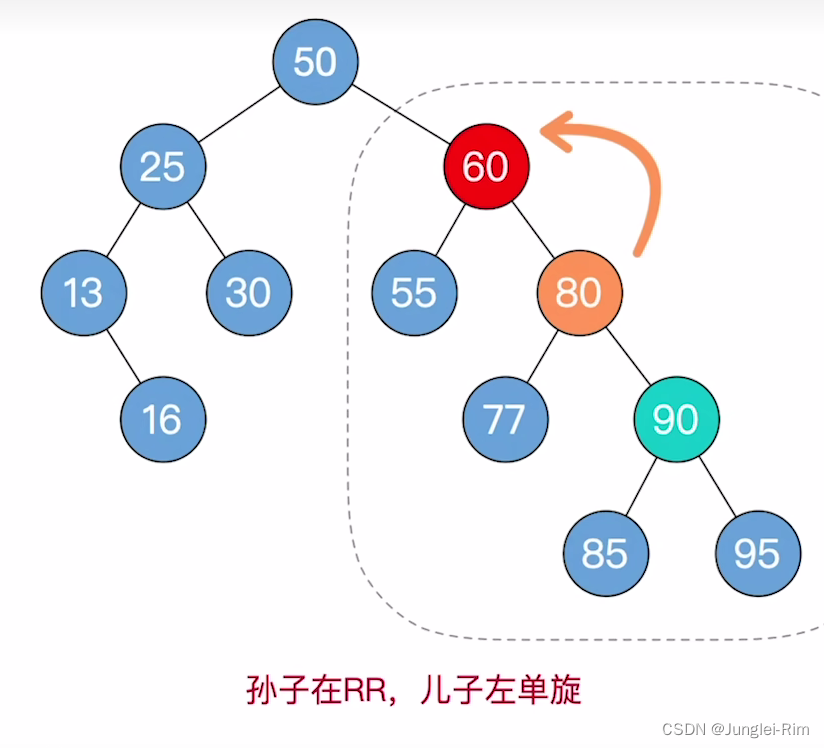
4 . 根据其树高最大的孙子结点的位置,调整平衡二叉树:(LL,RR,LR,RL四种情况)
- 孙子在LL:儿子右单旋
- 孙子在RR:儿子左单旋
- 孙子在LR:孙子先左旋,再右旋
- 孙子在RL:孙子先右旋,再左旋
具体二叉树旋转操作见博客:平衡二叉树的定义,插入操作以及插入新结点后的调整规则(ALV树)
5 . 如果调整后不平衡,则继续向上调整(进行第二步),直到二叉树平衡。
- 对最小不平衡子树的旋转可能导致树变矮,从而导致上层祖先不平衡(不平衡向上传递)
3.时间复杂度
平衡二叉树删除操作时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)。