目录

一、规范化理论

        1、规范化理论的基本概念

        2、Armstrong公理

        3、候选键

        4、范式

        5、模式分解

---

一、规范化理论

        1、规范化理论的基本概念

                非规范化的关系模式，可能存在的问题包括：数据冗余、更新异常、插入异常、删除异常。 

                下表可拆分为 学号、姓名、系号 和 系号、系名、系位置 两张表。

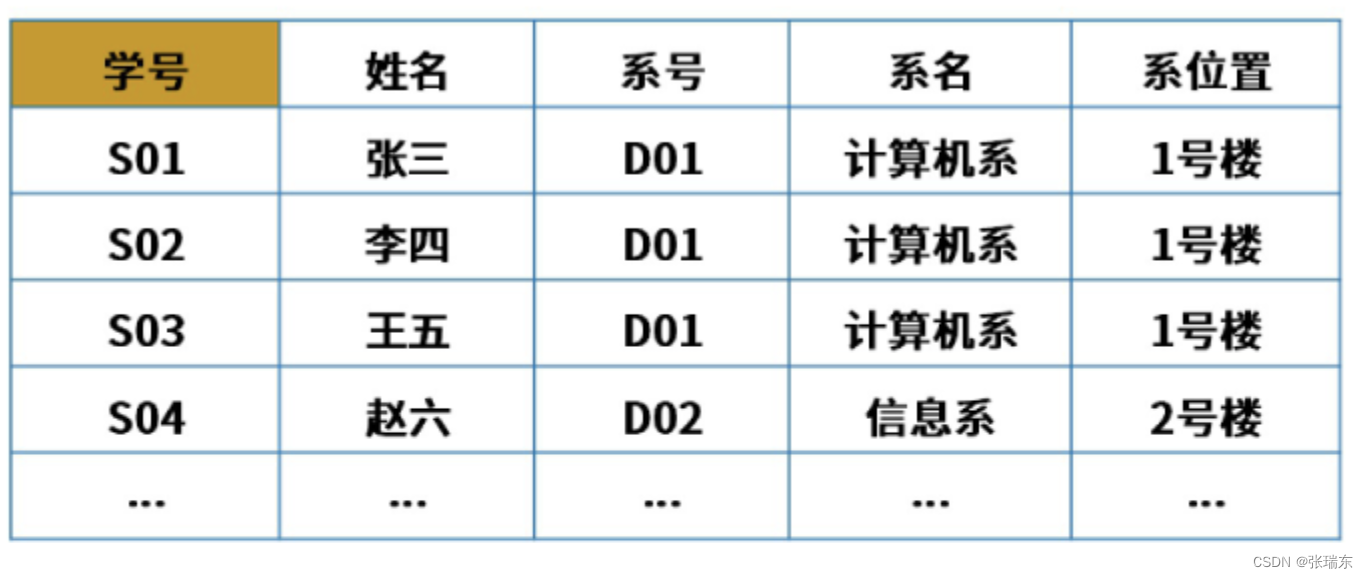
                设R(U)是属性U上的一个关系模式，X和Y是U的子集，r为R的任一关系，如果对于r中的任意两个元祖u，v，只要有u[X] = v[X]，就有u[Y] = v[Y]，则称X函数决定Y，或称Y函数依赖于X，记为X->Y。

 

        2、Armstrong公理

                关系模式R<U，F>来说有以下推理规则：

                A1.自反率（Reflexivity）：若Y⊆X⊆U，则X->Y成立。

                A2.增广率（Augmentation）：若Z⊆U且X->Y，则XZ -> YZ成立。

                A3.传递率（Transitivity）：若X->Y且Y->Z，则X->Z成立。

                根据A1，A2，A3这三条推理规则可以得到下面三条推理规则：

                合并规则：由X->Y，X->Z，有X->YZ。（A2，A3）

                伪传递规则：由X->Y，WY->Z，有XW->Z。（A2，A3）

                分解规则：由X->Y及Z⊆Y，有X->Z。（A1，A3）

        3、候选键

                主属性与非主属性：组成候选码的属性就是主属性，其他的就是非主属性。

                例如：在{A，B，C，D，E}中，候选码为 {AB，AC}，则主属性就是{A，B，C}

                找候选键的方式：

                （1）将关系模式的函数依赖关系用 “有向图” 的方式表示。

                （2）找入度为0的属性，并以该属性集合为起点，尝试遍历有向图，若能正常遍历图中所有节点，则该属性集即为关系模式的候选键。

                （3）若入度为0的属性集不能遍历图中所有结点，则需要尝试性的将一些中间节点（即有入度，也有出度的结点）并入入度为0的属性集中，直至该集合能遍历所有结点，集合为候选键。

        4、范式

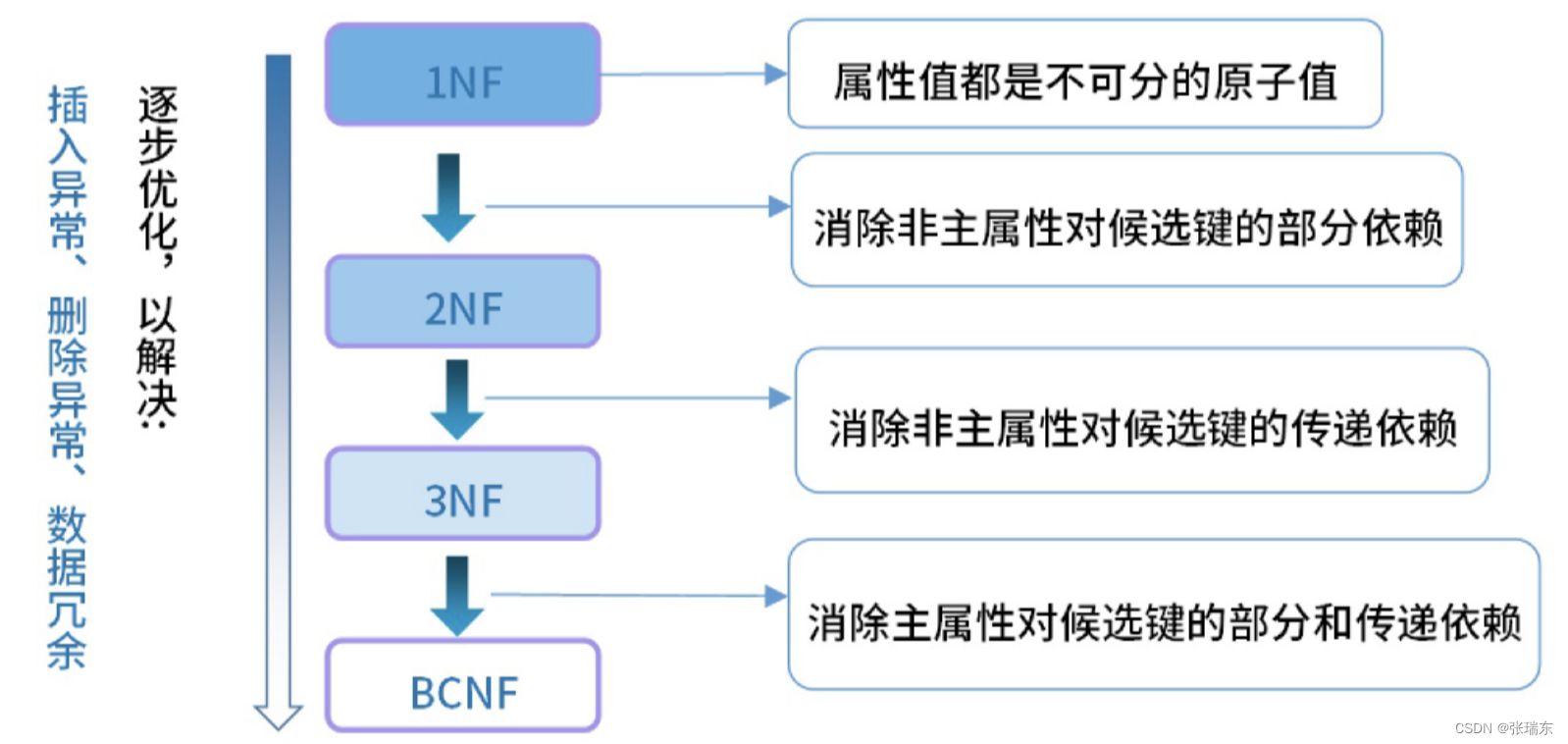
                （1）第一范式（1NF）：属性值都是不可分的原子值

                        在关系模式R中，当且仅当所有域只包含原子值，即每个属性都是不可再分的数据项，则称关系模式R是第一范式。 

                        答：将表字段改为系名称、教授人数、副教授人数。

 

                （2）第二范式（2NF）：消除非主属性对候选键的部分依赖

                        当且仅当实体E是第一范式（1NF），且每个非主属性完全依赖主键（不存在部分依赖）时，则称实体E是第二范式。                         答：将上表分为 { 学号、课程号、成绩 } 和 { 课程号、学分 } 两个表，可满足第二范式2NF。 

 

                （3）第三范式（3NF）：消除非主属性对候选键的传递依赖

                        当且仅当实体E是第二范式（2NF），且E中没有非主属性对候选键存在传递依赖时，则称实体E是第三范式。                         答：将上表分为 { 学号、姓名、系号 } 和 { 系号、系名、系位置 } 两个表，可满足第三范式3NF。 

 

                （4）第四范式（BCNF）：消除主属性对候选键的部分和传递依赖

                        设R是一个关系模式，F是它的依赖集，R属于BCNF当且仅当其F中每个依赖的决定因素必定包含某个候选码 

                        U = { S，T，J }，F= { T->J，SJ->T }  

                        答：候选键为 { ST、SJ }，主属性为 { S、T、J } ，没有非主属性，满足第三范式3NF，因为 T->J 所以不满足第四范式BCNF。 

        5、模式分解

               【保持函数依赖分解】

                设数据库模式p= { R1，R2，···，Rk } 是关系模式R的一个分解，F是R上的函数依赖集，p中每个模式Ri上的FD集是Fi。如果 { F1，F2，···，Fk } 与F是等价的（即相互逻辑蕴含），那么称分解p保持FD。

                答：因为拆分后A->B，B->C，符合之前的依赖关系，所以保持依赖。 

                答：因为拆分后A->B，B->C，由此能推出B->C，符合之前的依赖关系，所以保持依赖。 

                 答：因为拆分后A->B，A->C，无法推出B->C，不符合之前的依赖关系，所以保持依赖。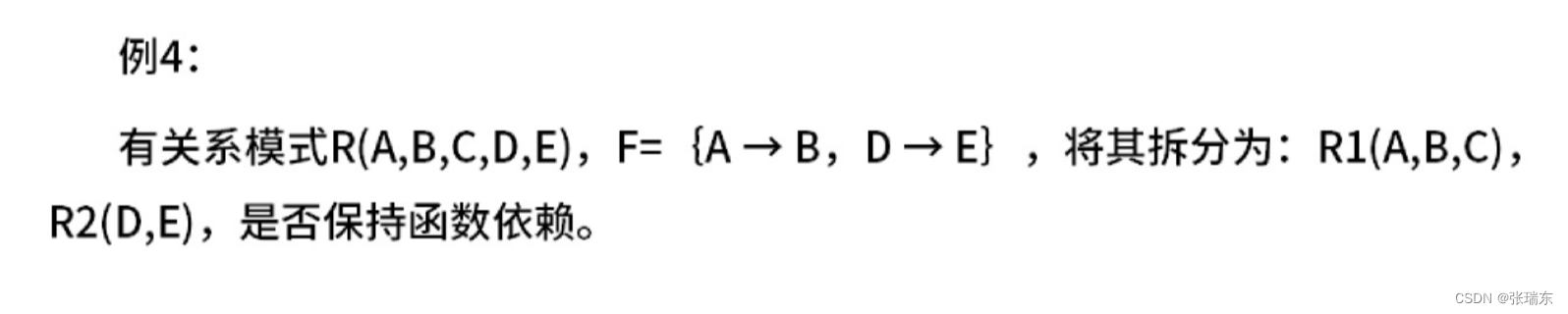 

                 答：因为拆分后A->B，A->C，D->E，符合之前的依赖关系，所以保持依赖，但它不是无损分解，是有损。

  

                【无损分解】

                什么是有损，什么又是无损？

                有损：不能还原。 无损：可以还原。

                无损链接分解：指将一个关系模式分解成若干个关系模式后，通过自然链接和投影等运算仍能还原到原来的关系模式。

                简单来说就是采用公式法，先做交集再做差集。（不过只适用于分解成两个关系模式）

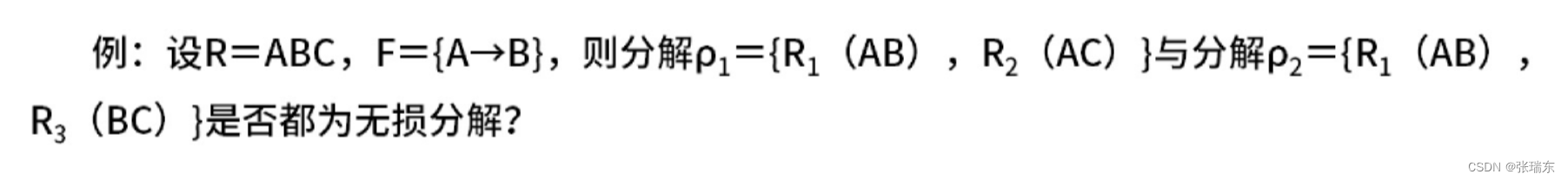
                答：R1∩R2得A，R1-R2得B，R2-R1得C，所以A->B，A->C，与F= { A->B } 有重合，p1是无损分解。

                        R1∩R3得B，R1-R3得A，R3-R1得C，所以B->A，B->C，与F= { A->B } 没有重合，p2是有损分解。

                解：因为传递依赖关系第一问选D。

                        分解后U1满足A->BC，U2满足B->D，D->E，所以保持函数依赖。U1∩U2得B，U1-U2得AC，U2-U1得DE，所以B->AC，B->DE，与F = { A->BC，B->D，D->E } 有重合，所以是无损连接。

                答：D、A。