---

前言

1. 图的应用
   1.1 最小生成树
   1.2 最短路径
   1.3 拓扑结构
   1.4 关键路径

---

一、图的应用

1. 最小生成树

1. 定义：从图中选取若干条边，将所有顶点连接起来，并且所选取的这些边的权值之和最小
   1).最小生成树的算法
   a. 普里姆算法
   b. 克鲁斯卡尔算法
2. 最小生成树性质
   （1）最小生成树树形不唯一；图中各权值互不相等时，G的最小生成树唯一；若无向图连通图边比顶点少1，即G本身就是一棵树，G的最小生成树就是本身
   （2）虽然最小生成树不唯一，但最小生成树边的权值之和唯一且最小
   （3）最小生成树边数为顶点数减1

普里姆（Prim）算法

1. 概念：算法从一个顶点开始，在此顶点对应的结点中寻找最小权值的结点连接，如此往复，直至满了为止，此时树必有n-1条边
   

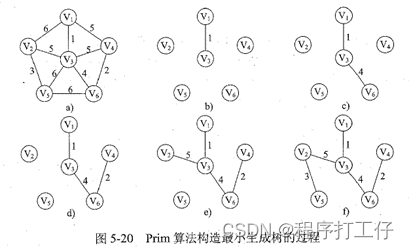
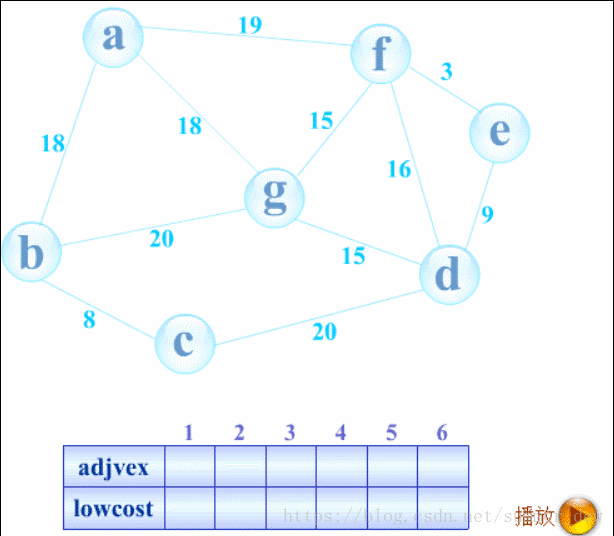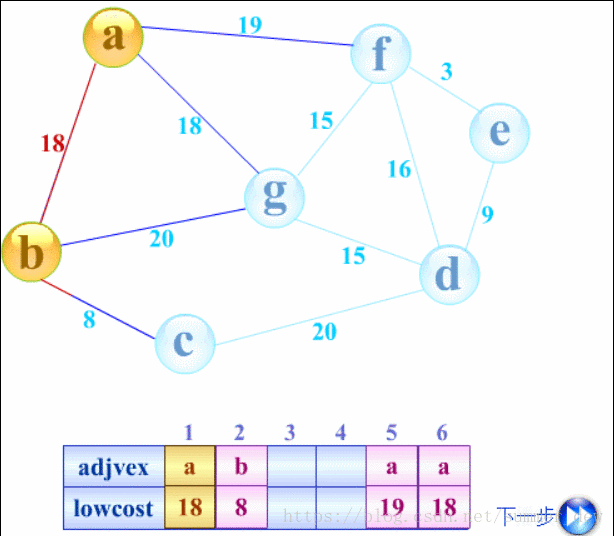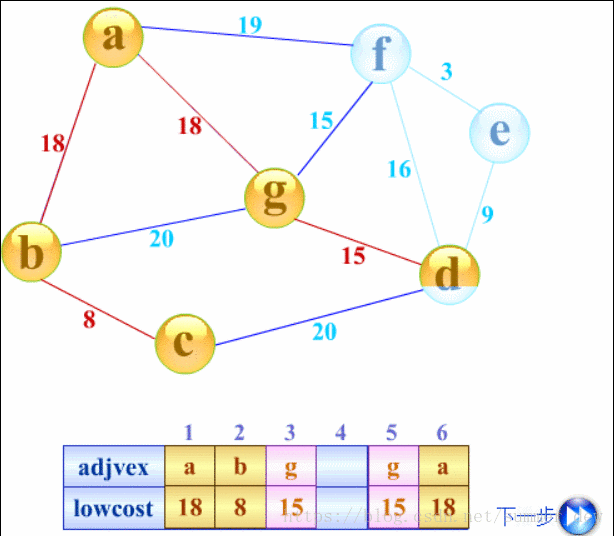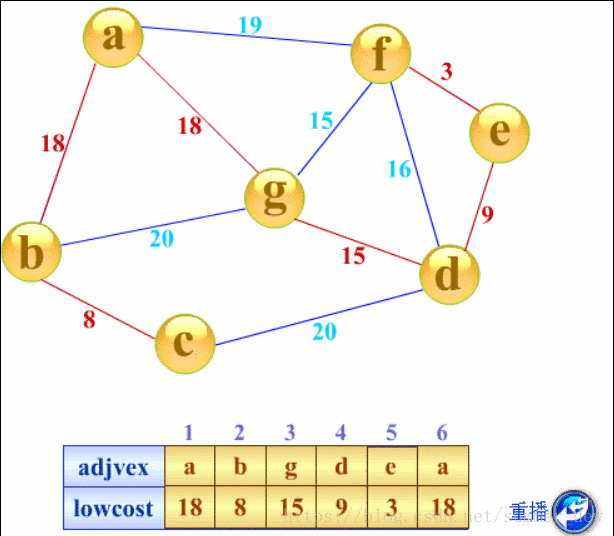
2. 时间复杂度：O(|V|²)，不依赖于|E|，适用于求解稠密图的最小生成树

克鲁斯卡尔（Kruskal）算法

1. 按权值递增序列选择合适的边来构造最小生成树，开始时，每个顶点构成一棵独立的树，T此时为仅含V各结点的森林，按G的边的权值递增顺序选择一条边，若这条边加入不构成回路，则将其加入，否则舍弃，直到含有n-1条边；构造时按网中权值由小到大的顺序，不断选取当前未被选取的边集中权值最小的边，选取n-1条边
   
   
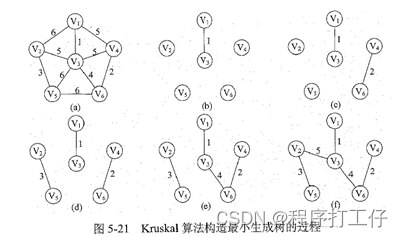
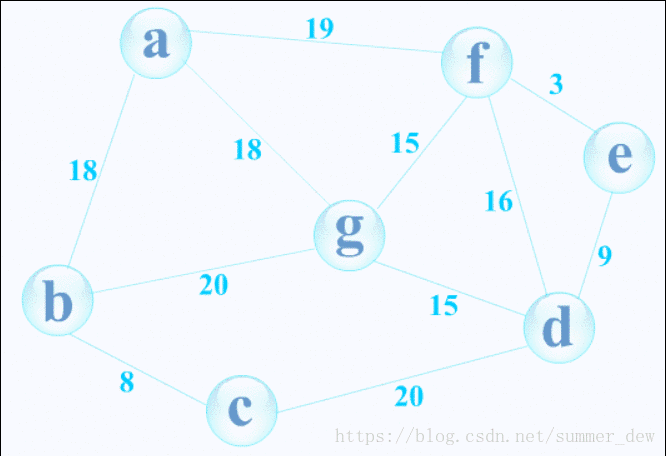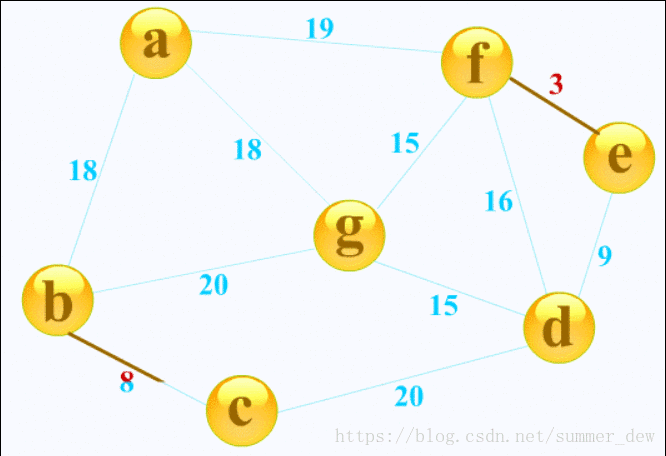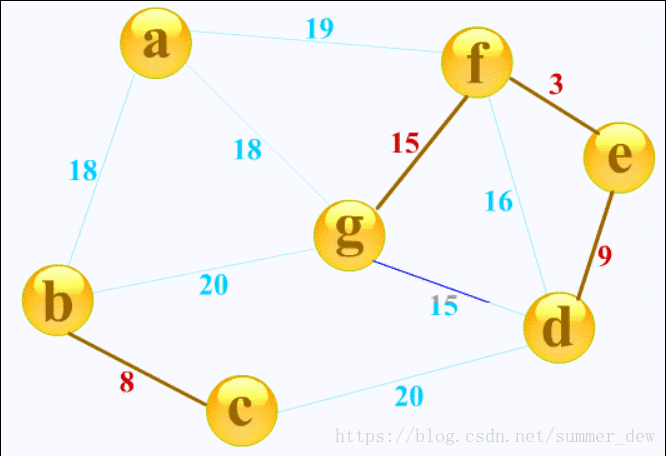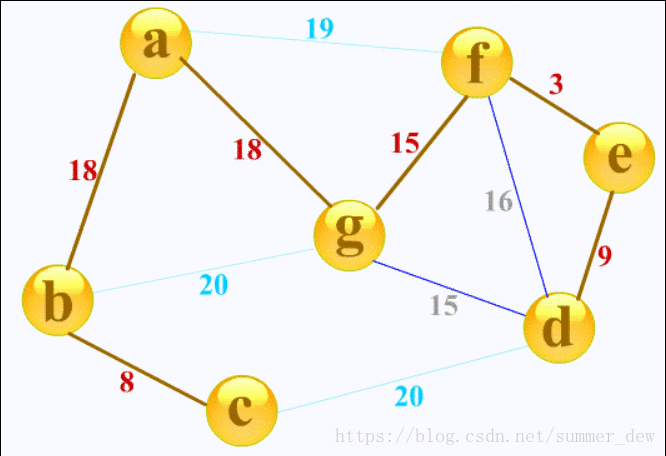
2. 时间复杂度：采用堆存放边的集合，O(|E|log|E|)，适用于边稀疏而顶点较多的图
   

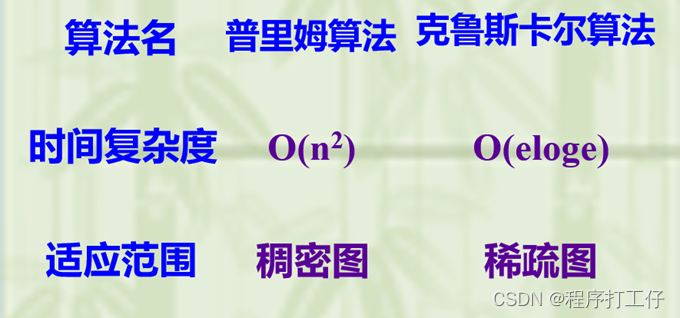
2. 最短路径

概念：对于带权图，路径上权值之和最小的叫最短路径

Dijkstra算法求单源最短路径

1. 概念：从某一顶点出发，求到另一顶点的最小路径（带权值），可以从一顶点出发挨个搜寻，每一趟都需要得到最短的路径，求的是一顶点到所有其他顶点的路径

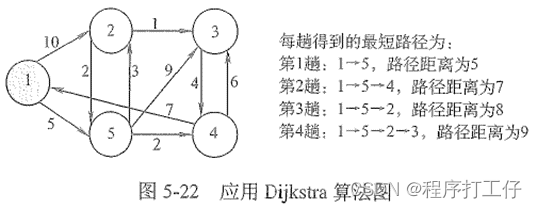
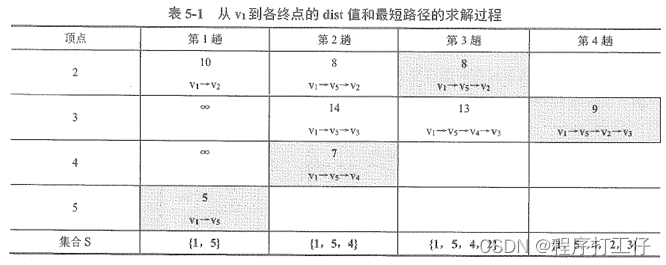
2. 时间复杂度：邻接矩阵为O(|V|²)，邻接表为O(|V|²)，若要找出所有结点之间最短距离，则时间复杂度为O(|V|³)
3. 注意：若有负权值，此算法不适用
4. Floyd算法求各顶点间最短路经过
   产生一个n阶方阵 （k从-1开始到n-1）表示从顶点vi到vj路径长度，k表示绕行第k个顶点运算步骤；初始时，vi和vj之间存在边，则以此边权值作为最短路径，若不存在边则以无穷作为权值；以后逐步加入顶点k作为中间顶点，若增加中间结点得到的路径比原路径减少了，则以此新路径代替原来路径

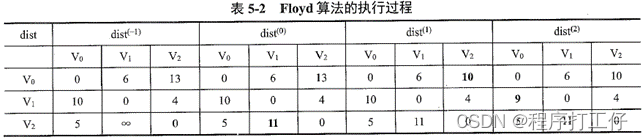
5. 时间复杂度：O(|V|³)
6. 注意：允许带负权值的边，但不允许包含带负权值的边组成的回路，也适用于带权无向图

3. 拓扑结构

1. 有向无环图：有向图中不存在环，称为DAG图
2. 拓扑排序
   （1）一个有向无环图顶点组成的序列满足下列条件
   ①每个顶点出现仅出现一次
   ②若顶点A排在B前面，则不存在从B到A的路径
   （2）对一个DAG图进行拓扑排序
   ①从DAG中选择一个没有前驱的顶点并输出
   ②从图中删除该顶点和所有以它为起点的有向边
   ③重复（1）（2）直到DAG图为空或者图中不存在无前驱顶点为止，而后一种情况说明有向图必存在环
   
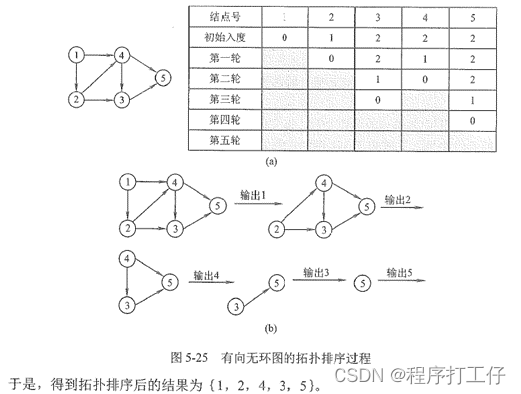
   （3）时间复杂度：O(|V|+|E|)
   （4）用拓扑排序算法处理DAG图时，注意：
   ①一个顶点有多个直接后继，拓扑排序不唯一；但若各个顶点已经排在一个线性有序序列中，每个顶点有唯一前驱后继关系，则结果唯一
   ②对于一般的图，若它的邻接矩阵是三角矩阵，则存在拓扑序列
   如果进行到某一步，无法找到无前趋的顶点，则说明此AOV网络中存在有向环路，遇到这种情况，拓扑排序就无法进行了。
   在算法中需要用定量的描述替代定性的概念
   没有前驱的顶点=入度为零的顶点
   删除顶点及以它为尾的弧=弧头顶点的入度减1

4. 关键路径

1. 相关概念
   源点：存在唯一的入度为0的顶点，叫源点
   汇点：存在唯一的，出度为0的顶点叫汇点
   关键路径：从源点到汇点的最长路径的长度，即为完成整个工程任务所需的时间，该路径称为关键路径。
   关键活动：关键路径上的活动叫做关键活动
2. AOE网
   （1）概念：在有向图中，用顶点表示事件,用弧表示活动，弧的权值表示活动所需的时间，这种有向无环图叫做边表示活动的网，简称AOE-网
   （2）AOE网性质：（1）只有某顶点表示的事件发生后，从该顶点出发的有向边所表示的活动才能开始（2）只有在进入某一顶点各有向边所代表的活动都已经结束时，该顶点所代表的事件才能发生
   （3）AOE网中只有一个源点（入度为0）表示工程开始，也只有一个汇点（出度为0）表示工程结束
   （4）只有路径上所有活动都完成了，整个工程才结束，从源点到汇点的最大路径长度的路径称为关键路径，关键路径上的活动叫关键活动（e(i)=l(i)）
   （5）最短时间就是关键路径长度，也就是关键路径上各活动花费开销之和
3. 求关键路径步骤
   （1）求AOE网中所有事件最早发生时间ve()
   （2）求AOE网中所有事件最迟发生时间vl()
   （3）求AOE网中所有活动最早开始时间e()
   （4）求AOE网中所有活动最迟开始时间l()
   （5）求AOE网中所有活动的差额d()，找出所有d()=0的活动构成关键路径

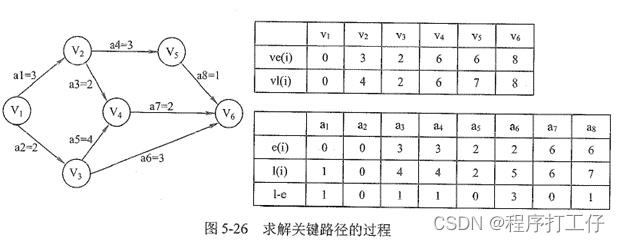
注：
（1）可以判断有向图是否有环：深度优先遍历、拓扑排序、关键路径
（2）不存在拓扑排序的有向图，必存在回路
（3）只有关键路径上所有活动时间同时减少，才能缩短工期

总结

1. 图的应用
   1.1 最小生成树
   1.2 最短路径
   1.3 拓扑结构
   1.4 关键路径