Java8实战-总结29
- 并行数据处理与性能
- 并行流
- 将顺序流转换为并行流
- 测量流性能
并行数据处理与性能
到目前为止,Stream接口最重要的好处是可以对这些集合执行操作流水线,能够自动利用计算机上的多个内核。
例如,在Java 7之前,并行处理数据集合非常麻烦。第一,需要明确地把包含数据的数据结构分成若干子部分。第二,要给每个子部分分配一个独立的线程。第三,需要在恰当的时候对它们进行同步来避免不希望出现的竞争条件,等待所有线程完成,最后把这些部分结果合并起来。Java 7引入了一个叫作分支/合并的框架,让这些操作更稳定、更不易出错。
Stream接口允许声明性地将顺序流变为并行流。了解并行流内部是如何工作的很重要,因为如果忽视这一方面,就可能因误用而得到意外的(很可能是错的)结果。
并行流
stream接口可以让你非常方便地处理它的元素:可以通过对收集源调用parallelStream方法来把集合转换为并行流。并行流就是一个把内容分成多个数据块,并用不同的线程分别处理每个数据块的流。这样一来,就可以自动把给定操作的工作负荷分配给多核处理器的所有内核,让它们都忙起来。
假设需要写一个方法,接受数字n作为参数,并返回从1到给定参数的所有数字的和。一个直接的方法是生成一个无穷大的数字流,把它限制到给定的数目,然后用对两个数字求和的Binaryoperator来归约这个流,如下所示:
public static long sequentialSum(long n) {
return Stream.iterate(1L, i -> i + 1) //生成自然数无限流
.limit(n) //限制到前n个数
.reduce(0L, Long::sum); //对所有数字求和来归纳流
用更为传统的Java术语来说,这段代码与下面的迭代等价:
public static long iterativesum(long n) {
long result = 0;
for(1ong i = 1L; i <= n; i++) {
result += i;
}
return result;
}
这似乎是利用并行处理的好机会,特别是n很大的时候。那怎么入手呢?要对结果变量进行同步吗?用多少个线程呢?谁负责生成数呢?谁来做加法呢?
用并行流的话,这问题就简单多了。
将顺序流转换为并行流
可以把流转换成并行流,从而让前面的函数归约过程(也就是求和)并行运行——对顺序流调用parallel方法:
public static long parallelSum(long n) {
return Stream.iterate(1L, i -> i + 1)
.limit(n)
·paralle1() //将流转换为并行流
.reduce(0L, Long::sum);
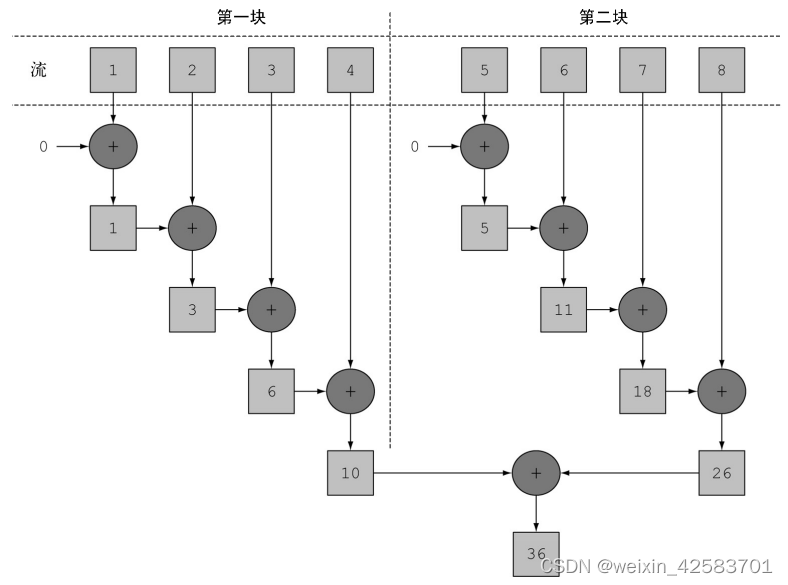
在上面的代码中的不同之处在于Stream在内部分成了几块。因此可以对不同的块独立并行进行归纳操作,如下图所示。最后,同一个归纳操作会将各个子流的部分归纳结果合并起来,得到整个原始流的归纳结果。
请注意,在现实中,对顺序流调用parallel方法并不意味着流本身有任何实际的变化。它在内部实际上就是设了一个boolean标志,表示你想让调用parallel之后进行的所有操作都并行执行。类似地,你只需要对并行流调用sequential方法就可以把它变成顺序流。请注意,你可能以为把这两个方法结合起来,就可以更细化地控制在遍历流时哪些操作要并行执行,哪些要顺序执行。例如,可以这样做:
stream.parallel()
.filter(...)
.sequential()
.map(...)
·parallel()
.reduce();
但最后一次parallel或sequential调用会影响整个流水线。在本例中,流水线会并行执行,因为最后调用的是它。
回到我们的数字求和练习,我们说过,在多核处理器上运行并行版本时,会有显著的性能提升。现在你有三个方法,用三种不同的方式(迭代式、顺序归纳和并行归纳)做完全相同的操作,让我们看看谁最快吧!
测量流性能
虽然声称并行求和方法应该比顺序和迭代方法性能好。然而在软件工程上,靠猜绝对不是什么好办法,特别是在优化性能时,你应该始终遵循三个黄金规则:测量,测量,再测量。为此,可以开发一个方法,如下所示,测量对前n个自然数求和的函数的性能:
public long measureSumPerf(Function<Long, Long> adder, long n) {
long fastest = Long.MAX_VALUE;
for(int i = 0; i < 10; i++) {
long start = System.nanoTime();
long sum = adder.apply(n);
long duration =(System.nanoTime() - start) / 1_000_000;
System.out.println("Result:"+ sum);
if(duration < fastest) fastest = duration;
}
return fastest;
}
这个方法接受一个函数和一个long作为参数。它会对传给方法的long应用函数10次,记录每次执行的时间(以毫秒为单位),并返回最短的一次执行时间。假设你把先前开发的所有方法都放进了一个名为ParallelStreams的类,你就可以用这个框架来测试顺序加法器函数对前一千万个自然数求和要用多久:
System.out.println("Sequential sum done in:" + measureSumPerf(ParallelStreams::sequentialSum,10_000_000) + " msecs");
请注意,我们对这个结果应持保留态度。影响执行时间的因素有很多,比如你的电脑支持多少个内核。你可以在自己的机器上跑一下这些代码。我们运行它,输出是这样的:
Sequential sum done in: 97 msecs
用传统for循环的迭代版本执行起来应该会快很多,因为它更为底层,更重要的是不需要对原始类型做任何装箱或拆箱操作。如果你试着测量它的性能,
System.out.println("Iterative sum done in:" +
measureSumPerf(ParallelStreams::iterativesum, 10_000_000) + " msecs");
将得到:
Iterative sum done in: 2 msecs
现在来对函数的并行版本做测试:
System.out.println("Parallel sum done in:" + measureSumPerf(ParallelStreams::parallelSum, 10_000_000) + " msecs");
看看会出现什么情况:
Parallel sum done in: 164 msecs
这相当令人失望,求和方法的并行版本比顺序版本要慢很多。如何解释这个意外的结果呢?这里实际上有两个问题:
iterate生成的是装箱的对象,必须拆箱成数字才能求和;- 我们很难把
iterate分成多个独立块来并行执行。
第二个问题更有意思一点,因为你必须意识到某些流操作比其他操作更容易并行化。具体来说,iterate很难分割成能够独立执行的小块,因为每次应用这个函数都要依赖前一次应用的结果,如下图所示。
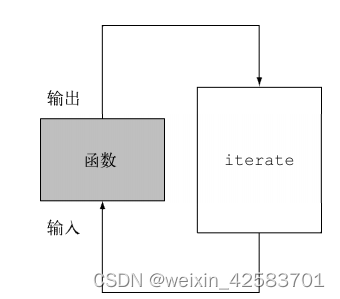
这意味着,在这个特定情况下,归纳进程不是像上面图中那样进行的;整张数字列表在归纳过程开始时没有准备好,因而无法有效地把流划分为小块来并行处理。把流标记成并行,你其实是给顺序处理增加了开销,它还要把每次求和操作分到一个不同的线程上。
这就说明了并行编程可能很复杂,有时候甚至有点违反直觉。如果用得不对(比如采用了一个不易并行化的操作,如iterate),它甚至可能让程序的整体性能更差,所以在调用那个看似神奇的parallel操作时,了解背后到底发生了什么是很有必要的。
使用更有针对性的方法
那到底要怎么利用多核处理器,用流来高效地并行求和呢?LongStream.rangeClosed方法与iterate相比有两个优点。
LongStream.rangeClosed直接产生原始类型的long数字,没有装箱拆箱的开销。LongStream.rangeClosed会生成数字范围,很容易拆分为独立的小块。例如,范围1~ 20可分为1~ 5、6~ 10、11~ 15和16~20。
让我们先看一下它用于顺序流时的性能如何,看看拆箱的开销到底要不要紧:
public static long rangedsum(long n) {
return LongStream.rangeclosed(1, n)
.reduce(OL, Long::sum);
}
这一次的输出是:
Ranged sum done in: 17 msecs
这个数值流比前面那个用iterate工厂方法生成数字的顺序执行版本要快得多,因为数值流避免了非针对性流那些没必要的自动装箱和拆箱操作。由此可见,选择适当的数据结构往往比并行化算法更重要。但要是对这个新版本应用并行流呢?
public static long parallelRangedsum(long n) {
return LongStream.rangeClosed(1, n)
·parallel()
.reduce(0L, Long::sum);
}
现在把这个函数传给测试方法:
System.out.println("Parallel range sum done in:" + measureSumPerf(ParallelStreams::parallelRangedsum, 10_000_000) + " msecs");
会得到:
Parallel range sum done in: 1 msecs
终于,得到了一个比顺序执行更快的并行归纳,因为这一次归纳操作可以像上面图中那样执行了。这也表明,使用正确的数据结构然后使其并行工作能够保证最佳的性能。
尽管如此,请记住,并行化并不是没有代价的。并行化过程本身需要对流做递归划分,把每个子流的归纳操作分配到不同的线程,然后把这些操作的结果合并成一个值。但在多个内核之间移动数据的代价也可能比想的要大,所以很重要的一点是要保证在内核中并行执行工作的时间比在内核之间传输数据的时间长。总而言之,很多情况下不可能或不方便并行化。然而,在使用并行Stream加速代码之前,必须确保用得对;如果结果错了,算得快就毫无意义了。