图论

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

如下就是一种逻辑上的图结构：

图是一种最复杂的数据结构，前面讲的数据结构都可以看成是图的特例。那为什么不都用图就好了，还要分那么多种数据结构呢？

这是因为很多时候不需要用到那么复杂的功能，图的很多特性都不具备，如果笼统地都称为图那么非常不利于沟通。你想你和别人沟通总不至于说这道题是考察一种特殊的图，这种图。。。。 这未免太啰嗦了，因此给其他图的特殊的图起了特殊的名字，这样就方便沟通了。直到遇到了非常复杂的情况，我们才会用到 ”真正“的图。

前面章节提到了数据结构就是为了算法服务的，数据结构就是存储数据用的，目的是为了更高效。 那么什么时候需要用图来存储数据，在这种情况图高效在哪里呢？答案很简单，那就是如果你用其他简单的数据结构无法很好地进行存储，就应该使用图了。 比如我们需要存储一种双向的朋友关系，并且这种朋友关系是多对多的，那就一定要用到图，因为其他数据结构无法模拟。

基本概念

无向图 & 有向图〔Undirected Graph & Deriected Graph〕

前面提到了二叉树完全可以实现其他树结构，类似地，有向图也完全可以实现无向图和混合图，因此有向图的研究一直是重点考察对象。

本文讲的所有图都是有向图。

前面提到了我们用连接两点的线表示相应两个事物间具有这种关系。因此如果两个事物间的关系是有方向的，就是有向图，否则就是无向图。比如：A 认识 B，那么 B 不一定认识 A。那么关系就是单向的，我们需要用有向图来表示。因为如果用无向图表示，我们无法区分 A 和 B 的边表示的是 A 认识 B 还是 B 认识 A。

习惯上，我们画图的时候用带箭头的表示有向图，不带箭头的表示无向图。

有权图 & 无权图〔Weighted Graph & Unweighted Graph〕

如果边是有权重的是有权图（或者带权图），否则是无权图（或不带权图）。那么什么是有权重呢？比如汇率就是一种有权重的逻辑图。1 货币 A 兑换 5 货币 B，那么我们 A 和 B 的边的权重就是 5。而像朋友这种关系，就可以看做一种不带权的图。

入度 & 出度〔Indegree & Outdegree〕

有多少边指向节点 A，那么节点 A 的入度就是多少。同样地，有多少边从 A 发出，那么节点 A 的出度就是多少。

仍然以上面的图为例，这幅图的所有节点的入度和出度都为 1。

路径 & 环〔路径：Path〕

• 有环图〔Cyclic Graph〕 上面的图就是一个有环图，因为我们从图中的某一个点触发，能够重新回到起点。这和现实中的环是一样的。
• 无环图〔Acyclic Graph〕

我可以将上面的图稍加改造就变成了无环图，此时没有任何一个环路。

连通图 & 强连通图

在无向图中，若任意两个顶点 i 与 j 都有路径相通，则称该无向图为连通图。

在有向图中，若任意两个顶点 i 与 j 都有路径相通，则称该有向图为强连通图。

生成树

一个连通图的生成树是指一个连通子图，它含有图中全部 n 个顶点，但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边，如果生成树中再添加一条边，则必定成环。在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树，其中代价和指的是所有边的权重和。

图的建立

一般图的题目都不会给你一个现成的图的数据结构。当你知道这是一个图的题目的时候，解题的第一步通常就是建图。

上面讲的都是图的逻辑结构，那么计算机中的图如何存储呢？

我们知道图是有点和边组成的。理论上，我们只要存储图中的所有的边关系即可，因为边中已经包含了两个点的关系。

这里我简单介绍两种常见的建图方式：邻接矩阵（常用，重要）和邻接表。

邻接矩阵（常见）〔Adjacency Matrixs〕

第一种方式是使用数组或者哈希表来存储图，这里我们用二维数组来存储。

使用一个 n * n 的矩阵来描述图 graph，其就是一个二维的矩阵，其中 graph[i][j] 描述边的关系。

一般而言，对于无权图我都用 graph[i][j] = 1 来表示 顶点 i 和顶点 j 之间有一条边，并且边的指向是从 i 到 j。用 graph[i][j] = 0 来表示 顶点 i 和顶点 j 之间不存在一条边。 对于有权图来说，我们可以存储其他数字，表示的是权重。

可以看出上图是对角线对称的，这样我们只需看一半就好了，这就造成了一半的空间浪费。

这种存储方式的空间复杂度为 O(n ^ 2)，其中 n 为顶点个数。如果是稀疏图（图的边的数目远小于顶点的数目），那么会很浪费空间。并且如果图是无向图，始终至少会有 50 % 的空间浪费。下面的图也直观地反应了这一点。

邻接矩阵的优点主要有：

1. 直观，简单。
2. 判断两个顶点是否连接，获取入度和出度以及更新度数，时间复杂度都是 O(1)

由于使用起来比较简单， 因此我的所有的需要建图的题目基本都用这种方式。

比如力扣 743. 网络延迟时间。 题目描述：

有 N 个网络节点，标记为 1 到 N。

给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。

现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。


示例：

输入：times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出：2


注意:

N 的范围在 [1, 100] 之间。
K 的范围在 [1, N] 之间。
times 的长度在 [1, 6000] 之间。
所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 0 <= w <= 100。

这是一个典型的图的题目，对于这道题，我们如何用邻接矩阵建图呢？

一个典型的使用二维数组构建邻接矩阵的代码：

graph = [[0]*n for _ in range(m)] # 新建一个 m * n 的二维矩阵

for fr, to, w in times:
    graph[fr-1][to-1] = w

这就构造了一个邻接矩阵。

邻接表〔Adjacency List〕

对于每个点，存储着一个链表，用来指向所有与该点直接相连的点。对于有权图来说，链表中元素值对应着权重。

例如在无向无权图中：

（图片来自 https://zhuanlan.zhihu.com/p/25498681）

可以看出在无向图中，邻接矩阵关于对角线对称，而邻接链表总有两条对称的边。

而在无向有权图中：

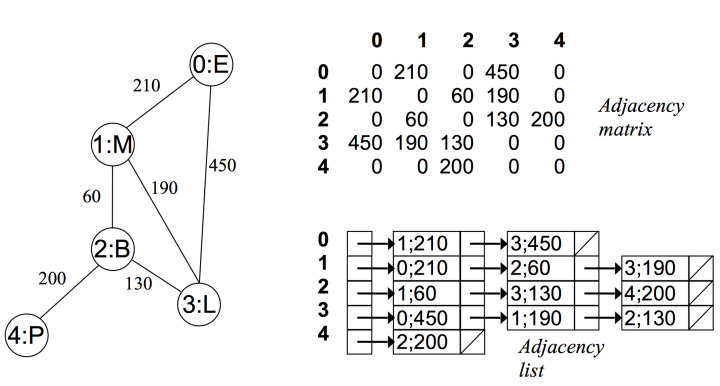
（图片来自 https://zhuanlan.zhihu.com/p/25498681）

使用邻接表建图：

    graph = collections.defaultdict(list)
    for fr, to, w in times:
        graph[fr - 1].append((to - 1, w))

这种方法的坏处是无法通过 graph[fr][to] 快速判断两个节点是否有边。好处是当边很少的时候更节省内存。

图的遍历

图建立好了，接下来就是要遍历了。

不管你是什么算法，肯定都要遍历的，一般有这两种方法：深度优先搜索，广度优先搜索（其他奇葩的遍历方式实际意义不大，没有必要学习）。

不管是哪一种遍历， 如果图有环，就一定要记录节点的访问情况，防止死循环。当然你可能不需要真正地使用一个集合记录节点的访问情况，比如使用一个数据范围外的数据原地标记，这样的空间复杂度会是 $O(1)$。

这里以有向图为例， 有向图也是类似，这里不再赘述。

关于图的搜索，后面的搜索专题也会做详细的介绍，因此这里就点到为止。

深度优先遍历〔Depth First Search, DFS〕

深度优先遍历图的方法是，从图中某顶点 v 出发， 不断访问邻居， 邻居的邻居直到访问完毕。

如上图， 如果我们使用 DFS，并且从 A 节点开始的话， 一个可能的的访问顺序是： A -> C -> B -> D -> F -> G -> E，当然也可能是 A -> D -> C -> B -> F -> G -> E 等，具体取决于你的代码，但他们都是深度优先的。

广度优先搜索〔Breadth First Search, BFS〕

广度优先搜索，可以被形象地描述为 “浅尝辄止”，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。

如上图， 如果我们使用 BFS，并且从 A 节点开始的话， 一个可能的的访问顺序是： A -> B -> C -> F -> E -> G -> D，当然也可能是 A -> B -> F -> E -> C -> G -> D 等，具体取决于你的代码，但他们都是广度优先的。

需要注意的是 DFS 和 BFS 只是一种算法思想，不是一种具体的算法。 因此其有着很强的适应性，而不是局限于特点的数据结构的，本文讲的图可以用，前面讲的树也可以用。实际上， 只要是非线性的数据结构都可以用。

常见算法

图的题目的算法比较适合套模板。

这里介绍几种常见的板子题。主要有：

• Dijkstra
• Floyd-Warshall
• 最小生成树（Kruskal & Prim） 目前此小节已经删除，觉得自己写的不够详细，之后补充完成会再次开放。
• A 星寻路算法
• 二分图（染色法）〔Bipartitie〕
• 拓扑排序〔Topological Sort〕

下面列举常见算法的模板。

以下所有的模板都是基于邻接矩阵建图。

强烈建议大家学习完专题篇的搜索之后再来学习下面经典算法。大家可以拿几道普通的搜索题目测试下，如果能够做出来再往下学习。推荐题目：最大化一张图中的路径价值

最短距离，最短路径

Dijkstra 算法

前置知识：堆（Heap）

DIJKSTRA 是单源最短路径算法，其中单源指的是起点就一个。如果我起点确定且只有一个，那么 DIJKSTRA 是非常适合的。当然如果起点有多个， 执行多次 DIJKSTRA 算法也可以。

DIJKSTRA 基本思想是广度优先遍历。实际上搜索的最短路算法基本思想都是广度优先，只不过具体的扩展策略不同而已。

DIJKSTRA 算法主要解决的是图中任意一点到图中另外任意一个点的最短距离，即单源最短路径。

Dijkstra 这个名字比较难记，大家可以简单记为DJ 算法，有没有好记很多？

比如给你几个城市，以及城市之间的距离。让你规划一条最短的从城市 a 到城市 b 的路线。

这个问题，我们就可以先将城市间的距离用图建立出来，然后使用 dijkstra 来做。那么 dijkstra 究竟如何计算最短路径的呢？

dj 算法的基本思想是贪心。从起点 start 开始，每次都遍历所有邻居，并从中找到距离最小的，本质上是一种广度优先遍历。这里我们借助堆这种数据结构，使得可以在 $logN$ 的时间内找到 cost 最小的点。

而如果使用普通的队列的话，其实是图中所有边权值都相同的特殊情况。

比如我们要找从点 start 到点 end 的最短距离。我们期望 dj 算法是这样被使用的。

比如一个图是这样的：

E -- 1 --> B -- 1 --> C -- 1 --> D -- 1 --> F
 \                                         /\
  \                                        ||
    -------- 2 ---------> G ------- 1 ------

我们使用邻接矩阵来构造：

G = {
    "B": [["C", 1]],
    "C": [["D", 1]],
    "D": [["F", 1]],
    "E": [["B", 1], ["G", 2]],
    "F": [],
    "G": [["F", 1]],
}

shortDistance = dijkstra(G, "E", "C")
print(shortDistance)  # E -- 3 --> F -- 3 --> C == 6

具体算法：

1. 初始化堆。堆里的数据都是 (cost, v) 的二元祖，其含义是“从 start 走到 v 的距离是 cost”。因此初始情况，堆中存放元组 (0, start)
2. 从堆中 pop 出来一个 (cost, v)，第一次 pop 出来的一定是 (0, start)。 如果 v 被访问过了，那么跳过，防止环的产生。
3. 如果 v 是 我们要找的终点，直接返回 cost，此时的 cost 就是从 start 到 该点的最短距离
4. 否则，将 v 的邻居入堆，即将 (neibor, cost + c) 加入堆，含义是从 start 到 neibor 最短距离是 cost。其中 neibor 为 v 的邻居， c 为 v 到 neibor 的距离（也就是转移的代价）。

重复执行 2 - 4 步

代码模板：

Python

import heapq


def dijkstra(graph, start, end):
    # 堆里的数据都是 (cost, i) 的二元祖，其含义是“从 start 走到 i 的距离是 cost”。
    heap = [(0, start)]
    visited = set()
    while heap:
        (cost, u) = heapq.heappop(heap)
        if u in visited:
            continue
        visited.add(u)
        if u == end:
            return cost
        for v, c in graph[u]:
            if v in visited:
                continue
            next = cost + c
            heapq.heappush(heap, (next, v))
    return -1

JavaScript

const dijkstra = (graph, start, end) => {
  const visited = new Set()
  const minHeap = new MinPriorityQueue();
  //注：此处new MinPriorityQueue()用了LC的内置API，它的enqueue由两个部分组成：
  //element 和 priority。
  //堆会按照priority排序，可以用element记录一些内容。
  minHeap.enqueue(startPoint, 0)

  while(!minHeap.isEmpty()){
    const {element, priority} = minHeap.dequeue();
    //下面这两个变量不是必须的，只是便于理解
    const curPoint = element;
    const curCost = priority;

    if(curPoint === end) return curCost;
    if(visited.has(curPoint)) continue;
    visited.add(curPoint);

    if(!graph[curPoint]) continue;
    for(const [nextPoint, nextCost] of graph[curPoint]){
      if(visited.has(nextPoint)) continue;
      //注意heap里面的一定是从startPoint到某个点的距离；
      //curPoint到nextPoint的距离是nextCost；但curPoint不一定是startPoint。
      const accumulatedCost = nextCost + curCost;
      minHeap.enqueue(nextPoint, accumulatedCost);
    }
  }
  return -1
}

会了这个算法模板， 你就可以去 AC 743. 网络延迟时间 了。

这里提供完整代码供大家参考：

Python

class Solution:
    def dijkstra(self, graph, start, end):
        heap = [(0, start)]
        visited = set()
        while heap:
            (cost, u) = heapq.heappop(heap)
            if u in visited:
                continue
            visited.add(u)
            if u == end:
                return cost
            for v, c in graph[u]:
                if v in visited:
                    continue
                next = cost + c
                heapq.heappush(heap, (next, v))
        return -1
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        graph = collections.defaultdict(list)
        for fr, to, w in times:
            graph[fr - 1].append((to - 1, w))
        ans = -1
        for to in range(N):
            dist = self.dijkstra(graph, K - 1, to)
            if dist == -1: return -1
            ans = max(ans, dist)
        return ans

JavaScript

const networkDelayTime = (times, n, k) => {
    //咳咳这个解法并不是Dijkstra在本题的最佳解法
    const graph = {};
    for(const [from, to, weight] of times){
        if(!graph[from]) graph[from] = [];
        graph[from].push([to, weight]);
    }

    let ans = -1;
    for(let to = 1; to <= n; to++){
        let dist = dikstra(graph, k, to)
        if(dist === -1) return -1;
        ans = Math.max(ans, dist);
    }
    return ans;
};

const dijkstra = (graph, startPoint, endPoint) => {
  const visited = new Set()
  const minHeap = new MinPriorityQueue();
  //注：此处new MinPriorityQueue()用了LC的内置API，它的enqueue由两个部分组成：
  //element 和 priority。
  //堆会按照priority排序，可以用element记录一些内容。
  minHeap.enqueue(startPoint, 0)

  while(!minHeap.isEmpty()){
    const {element, priority} = minHeap.dequeue();
    //下面这两个变量不是必须的，只是便于理解
    const curPoint = element;
    const curCost = priority;
    if(visited.has(curPoint)) continue;
    visited.add(curPoint)
    if(curPoint === endPoint) return curCost;

    if(!graph[curPoint]) continue;
    for(const [nextPoint, nextCost] of graph[curPoint]){
      if(visited.has(nextPoint)) continue;
      //注意heap里面的一定是从startPoint到某个点的距离；
      //curPoint到nextPoint的距离是nextCost；但curPoint不一定是startPoint。
      const accumulatedCost = nextCost + curCost;
      minHeap.enqueue(nextPoint, accumulatedCost);
    }
  }
  return -1
}

DJ 算法的时间复杂度为 $vlogv+e$，其中 v 和 e 分别为图中的点和边的个数。

细心的同学可能发现了，说好的单源最短路径呢？为什么这个算法只计算出了单起点到单个终点的最短路径呢？ 不能计算出所有其他节点的最短距离么? 即如果是计算一个点到图中所有点的距离呢？我们的算法会有什么样的调整？

提示：你可以使用一个 dist 哈希表记录开始点到每个点的最短距离来完成。想出来的话，可以用力扣 882 题去验证一下哦~ 这里提供一个使用 dist 的 python 代码供大家参考。

def dijkstra(s, e, g):
    h = [(0, s)]
    # dist[u] = w 表示从 s 到 u 的最短距离为 w
    dist = collections.defaultdict(int)
    while h:
        cost, cur = heapq.heappop(h)
        if cost > dist[cur]: continue
        for nxt, v in g[cur]:
            if cost+v >= dist[nxt]: continue
            dist[nxt] = cost+v
            heapq.heappush(h, (cost+v, nxt))
    return dist[e]

在一些题目中使用 dist 很有用，比如 Path-to-Maximize-Probability-to-Destination

值得注意的是， Dijkstra 无法处理边权值为负的情况。即如果出现负权值的边，那么答案可能不正确。而基于动态规划算法的最短路（下文会讲）则可以处理这种情况。

Floyd-Warshall 算法

前置知识：动态规划

Floyd-Warshall 可以解决任意两个点距离，即多源最短路径，这点和 dj 算法不一样。

除此之外，贝尔曼-福特算法也是解决最短路径的经典动态规划算法，这点和 dj 也是不一样的，dj 是基于贪心的。

这个算法很有用。 不仅仅是其可以解决任意两个点距离，而是其思想很有用，在解决图论问题中发挥很大的作用。

这个思想指的是枚举中间点思想，比如我想求两个点 fr, to 之间的最短距离，那么我就可以枚举中间点 mid，那么 fr 到 to 的距离就是 fr 经过 mid 到 to 的距离集合中的最小值（中间点有 n - 2 个，枚举 n - 2 次即可，其中 n 为联通集合大小），这其实就是后面专题篇的动态规划思想。 推荐题目 6032. 得到要求路径的最小带权子图 这道题可以抽象为 src1 和 src2 到中间点 mid 的距离 + 中间点到 dest 的距离。枚举 mid 即可得到达到。为了枚举 mid ，我们需要预处理出点与点的距离信息。这道题由于我们只需要知道 src1，src2，dest 三个点到其他所有点的最短距离，而不需要任意两个点的最短距离，因此使用上面讲到的 dijkstra 是合适的。 不过这个枚举中间点的思想确确实实和 Floyd-Warshall 类似。

算法用一句话来描述就是如果要计算两点的距离，那么我们可以枚举所有中间点，用最小的代价更新答案。

简单来说就是： i 到 j 的最短路径 = 所有 i 到 k 的最短路径 + k 到 j 的最短路径的最小值。其中 k 就是中间节点。我们可以枚举 k，（k 可能是除了 i 和 j 的其他所有点）然后更新答案。

如下图：

u 到 v 的最短距离是 u 到 x 的最短距离 + x 到 v 的最短距离。上图 x 是 u 到 v 的必经之路，如果不是的话，我们需要多个中间节点的值，并取最小的。

算法的正确性不言而喻，因为从 i 到 j，要么直接到，要么经过图中的另外一个点 k，中间节点 k 可能有多个，经过中间点的情况取出最小的，自然就是 i 到 j 的最短距离。

因此枚举 k，就可以得到答案。如果需要求任意两点的最短距离，则可以在枚举 k 的循环内部增加两层循环，分别枚举 i 和 j 即可。

枚举 k 的顺序一定是最外层，而枚举 i 和 j 的顺序可以互换。如果还是对此不理解，建议学习一下我们的《模拟，枚举与递推》章节。

相比上面的 dijkstra 算法， 由于其计算过程会把中间运算结果保存起来防止重复计算，因此其特别适合求图中任意两点的距离，比如力扣的 1462. 课程安排 IV。除了这个优点。下文要讲的贝尔曼-福特算法相比于此算法最大的区别在于本算法是多源最短路径，而贝尔曼-福特则是单源最短路径。不管是复杂度和写法， 贝尔曼-福特算法都更简单，我们后面给大家介绍。

当然就不是说贝尔曼算法以及上面的 dijkstra 就不支持多源最短路径，你只需要加一个 for 循环枚举所有的起点罢了。

还有一个非常重要的点是 Floyd-Warshall 算法由于使用了动态规划的思想而不是贪心，因此其可以处理负权重的情况，这点需要大家尤为注意。 动态规划的详细内容请参考之后的动态规划专题和背包问题。

思考题： 最长无环路径可以用动态规划来解么？

该算法的时间复杂度是 $O(N^3)$，空间复杂度是 $O(N^2)$，其中 N 为顶点个数。

代码模板：

Python

# graph 是邻接矩阵，n 是顶点个数
# graph 形如： graph[u][v] = w

def floyd_warshall(graph, n):
    dist = [[float("inf") for _ in range(n)] for _ in range(n)]

    for i in range(n):
        for j in range(n):
            dist[i][j] = graph[i][j]

    # check vertex k against all other vertices (i, j)
    for k in range(n):
        # looping through rows of graph array
        for i in range(n):
            # looping through columns of graph array
            for j in range(n):
                if (
                    dist[i][k] != float("inf")
                    and dist[k][j] != float("inf")
                    and dist[i][k] + dist[k][j] < dist[i][j]
                ):
                    dist[i][j] = dist[i][k] + dist[k][j]
    return dist

JavaScript

const floydWarshall = (graph, v)=>{
  const dist = new Array(v).fill(0).map(() => new Array(v).fill(Number.MAX_SAFE_INTEGER))

  for(let i = 0; i < v; i++){
    for(let j = 0; j < v; j++){
      //两个点相同，距离为0
      if(i === j) dist[i][j] = 0;
      //i 和 j 的距离已知
      else if(graph[i][j]) dist[i][j] = graph[i][j];
      //i 和 j 的距离未知，默认是最大值
      else dist[i][j] = Number.MAX_SAFE_INTEGER;
    }
  }

  //检查是否有一个点 k 使得 i 和 j 之间距离更短，如果有，则更新最短距离
  for(let k = 0; k < v; k++){
    for(let i = 0; i < v; i++){
      for(let j = 0; j < v; j++){
        dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j])
      }
    }
  }
  return 看需要
}

我们回过头来看下如何套模板解决 力扣的 1462. 课程安排 IV，题目描述：

你总共需要上 n 门课，课程编号依次为 0 到 n-1 。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。

对于每个查询对 queries[i] ，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。



示例 1：



输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。
示例 2：

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。
示例 3：



输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]
示例 4：

输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]
示例 5：

输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]


提示：

2 <= n <= 100
0 <= prerequisite.length <= (n * (n - 1) / 2)
0 <= prerequisite[i][0], prerequisite[i][1] < n
prerequisite[i][0] != prerequisite[i][1]
先修课程图中没有环。
先修课程图中没有重复的边。
1 <= queries.length <= 10^4
queries[i][0] != queries[i][1]

这道题也可以使用 Floyd-Warshall 来做。 你可以这么想， 如果从 i 到 j 的距离大于 0，那不就是先修课么。而这道题数据范围 queries 大概是 10 ^ 4 ， 用上面的 dijkstra 算法肯定超时，，因此 Floyd-Warshall 算法是明智的选择。

我这里直接套模板，稍微改下就过了。完整代码： Python

class Solution:
    def Floyd-Warshall(self, dist, v):
        for k in range(v):
            for i in range(v):
                for j in range(v):
                    dist[i][j] = dist[i][j] or (dist[i][k] and dist[k][j])

        return dist

    def checkIfPrerequisite(self, n: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
        graph = [[False] * n for _ in range(n)]
        ans = []

        for to, fr in prerequisites:
            graph[fr][to] = True
        dist = self.Floyd-Warshall(graph, n)
        for to, fr in queries:
            ans.append(bool(dist[fr][to]))
        return ans

JavaScript

//咳咳这个写法不是本题最优
var checkIfPrerequisite = function(numCourses, prerequisites, queries) {
    const graph = {}
    for(const [course, pre] of prerequisites){
        if(!graph[pre]) graph[pre] = {}
        graph[pre][course] = true
    }

    const ans = []

    const dist = Floyd-Warshall(graph, numCourses)
    for(const [course, pre] of queries){
        ans.push(dist[pre][course])
    }

    return ans
};

var Floyd-Warshall = function(graph, n){
    dist = Array.from({length: n + 1}).map(() => Array.from({length: n + 1}).fill(false))
    for(let k = 0; k < n; k++){
        for(let i = 0; i < n; i++){
            for(let j = 0; j < n; j++){
                if(graph[i] && graph[i][j]) dist[i][j] = true
                if(graph[i] && graph[k]){
                    dist[i][j] = (dist[i][j])|| (dist[i][k] && dist[k][j])
                }else if(graph[i]){
                    dist[i][j] = dist[i][j]
                }
            }
        }
    }
    return dist
}

如果这道题你可以解决了，我再推荐一道题给你 1617. 统计子树中城市之间最大距离，国际版有一个题解代码挺清晰，挺好理解的，只不过没有使用状态压缩性能不是很好罢了，地址：https://leetcode.com/problems/count-subtrees-with-max-distance-between-cities/discuss/1136596/Python-Floyd-Warshall-and-check-all-subtrees

图上的动态规划算法大家还可以拿这个题目来练习一下。

• 787. K 站中转内最便宜的航班

贝尔曼-福特算法

和上面 DJ 算法类似，这种解法主要解决单源最短路径，即图中某一点到其他点的最短距离。

基本思想和 Floyd-Warshall 类似，其基本思想也是动态规划。

这种算法我个人使用的非常少，实际刷题可以不使用，强烈建议大家学习好上面两种最短路算法，这里简单介绍一下贝尔曼-福特算法。

核心算法为：

• 初始化起点距离为 0
• 对图中的所有边进行若干次处理，直到稳定。处理的依据是：对于每一个有向边 (u,v)，如果 dist[u] + w 小于 dist[v]，那么意味着我们找到了一条到达 v 更近的路，更新之。
• 上面的若干次的上限是顶点 V 的个数，因此不妨直接进行 n 次处理。
• 最后检查一下是否存在负边引起的环。（注意）

举个例子。对于如下的一个图，存在一个 B -> C -> D -> B，这样 B 到 C 和 D 的距离理论上可以无限小。我们需要检测到这一种情况，并退出。

此算法时间复杂度：$O(V\ast E)$， 空间复杂度：$O(V)$。

代码示例：
Python

# return -1 for not exsit
# else return dis map where dis[v] means for point s the least cost to point v
def bell_man(edges, s):
    dis = defaultdict(lambda: math.inf)
    dis[s] = 0
    for _ in range(n):
        for u, v, w in edges:
            if dis[u] + w < dis[v]:
                dis[v] = dis[u] + w

    for u, v, w in edges:
        if dis[u] + w < dis[v]:
            return -1

    return dis

JavaScript

const BellmanFord = (edges, startPoint)=>{
  const n = edges.length;
  const dist = new Array(n).fill(Number.MAX_SAFE_INTEGER);
  dist[startPoint] = 0;

  for(let i = 0; i < n; i++){
    for(const [u, v, w] of edges){
        if(dist[u] + w < dist[v]){
            dist[v] = dist[u] + w;
        }
    }
  }

  for(const [u, v, w] of edges){
    if(dist[u] + w < dist[v]) return -1;
  }

  return dist
}

推荐阅读：

• bellman-ford-algorithm

题目推荐：

• Best Currency Path

拓扑排序

拓扑排序很常见，只要是关系可以描述成图，并且你需要对其进行编排，就会涉及到拓扑排序。比如你有几个构建任务，彼此可能有依赖，如何安排任务这就是一个拓扑排序问题。

在计算机科学领域，有向图的拓扑排序是对其顶点的一种线性排序，使得对于从顶点 u 到顶点 v 的每个有向边 u->v， u 在排序中都在之前。当且仅当图中没有定向环时（即有向无环图），才有可能进行拓扑排序。

典型的题目就是给你一堆课程，课程之间有先修关系，让你给出一种可行的学习路径方式，要求先修的课程要先学。任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内，构建任何有向无环图的拓扑排序。

如果让我们自己生成图的拓扑排序结构，你会怎么做？

朴素的思路就是依次遍历图中的每一个节点，对于每一个节点 v，我们都沿着它继续遍历它的邻居 u。那我们要做的无非就是把遍历的信息存到一个数据结构上。

比如我们遍历节点 v1, 发现它的邻居是 u1，u2，u3。那就可以更新信息，将:

v1 -> u1
v1 -> u2
v1 -> u3

更新进我们的数据结构中。

接下来，我们遍历节点 u1，发现 u1 可以到 u5。那就可以更新信息，将:

u1 -> u5

更新进我们的数据结构中。

结合上一步更新的数据结构，我们可以得到如下的信息：

v1 -> u1 -> u5
v1 -> u2
v1 -> u3

这里有三个路径，长度分别为 3,2,2

等到所有的路径信息都更新好了，问题也就解决了。

上面只考虑了没有环的情况，如果图中有环，那么是无法形成拓扑排序的，这点需要注意。

另外还有一个关键问题。如果存在一条边：

u4 -> u1

此时理论上的数据结构需要变为：

v1 -> u1 -> u5
v1 -> u2
v1 -> u3
u4 -> u1 -> u5

而如果第四条路径u4 -> u1 -> u5 中的 u1 -> u5 是在处理 u4 -> u1 的时候重新计算的。那么时间复杂度就很高了。

复杂度会高到 $O((V+E{)}^2)$

我们如何处理呢？

那就是利用已经计算好的信息，而不是重新计算。这是经典的拓扑排序算法的核心。优化后仅仅需要枚举所有点和边，因此复杂度为 $V+E$，其中 V 和 E 为图的点和边的个数。具体可以参考后面要讲的 Kahn 算法。

同时这提示我们，如果一道图的题当前节点的信息需要根据祖先节点计算出来，那么朴素的平方算法可能会超时。使用类似这里介绍的拓扑排序算法可以降低复杂度到和图的边数与顶点数之和线性相关。 比如：5300. 有向无环图中一个节点的所有祖先 就是需要结合祖先节点的计算结果计算当前节点，那么朴素的平方思路会超时（结合题目数据范围也知道这一点），因此拓扑排序的思路就应该被想到。

Kahn 算法

这个解法是基于 BFS 的。同样有基于 DFS 的解法，这里不再介绍，感兴趣的了解一下。

简单来说，假设 L 是存放结果的列表。

1. 先找到那些入度为零的节点，把这些节点放到 L 中，因为这些节点没有任何的父节点。
2. 然后把与这些节点相连的边从图中去掉，再寻找图中的入度为零的节点。
3. 对于新找到的这些入度为零的节点来说，他们的父节点已经都在 L 中了，所以也可以放入 L。
4. 重复上述操作，直到找不到入度为零的节点。如果此时 L 中的元素个数和节点总数相同，说明排序完成；如果 L 中的元素个数和节点总数不同，说明原图中存在环，无法进行拓扑排序。

def topologicalSort(graph):
    """
    Kahn's Algorithm is used to find Topological ordering of Directed Acyclic Graph
    using BFS
    """
    indegree = [0] * len(graph)
    queue = collections.deque()
    topo = []
    cnt = 0

    for key, values in graph.items():
        for i in values:
            indegree[i] += 1

    for i in range(len(indegree)):
        if indegree[i] == 0:
            queue.append(i)

    while queue:
        vertex = queue.popleft()
        cnt += 1
        topo.append(vertex)
        for x in graph[vertex]:
            indegree[x] -= 1
            if indegree[x] == 0:
                queue.append(x)

    if cnt != len(graph):
        print("Cycle exists")
    else:
        print(topo)


# Adjacency List of Graph
graph = {0: [1, 2], 1: [3], 2: [3], 3: [4, 5], 4: [], 5: []}
topologicalSort(graph)

令 V 和 E 分别为图的顶点数和边数。那么：

• 时间复杂度：$O(V+E)$
• 空间复杂度：$O(V+E)$

推荐题目：

• 207. 课程表
• 1203. 项目管理
• 2115. 从给定原材料中找到所有可以做出的菜

最小生成树

首先我们来看下什么是生成树。

首先生成树是原图的一个子图，它本质是一棵树，这也是为什么叫做生成树，而不是生成图的原因。其次生成树应该包括图中所有的顶点。 如下图由于没有包含所有顶点，换句话说所有顶点没有在同一个联通域，因此不是一个生成树。

黄色顶点没有包括在内

你可以将生成树看成是根节点不确定的多叉树，由于是一棵树，那么一定不包含环。如下图就不是生成树。

因此不难得出，最小生成树的边的个数是 n - 1，其中 n 为顶点个数。 4130fdaf1 接下来我们看下什么是最小生成树。

最小生成树是在生成树的基础上加了最小关键字，是最小权重生成树的简称。从这句话也可以看出，最小生成树处理正是有权图。生成树的权重是其所有边的权重和，那么最小生成树就是权重和最小的生成树，由此可看出，不管是生成树还是最小生成树都可能不唯一。

最小生成树在实际生活中有很强的价值。比如我要修建一个地铁，并覆盖 n 个站，这 n 个站要互相都可以到达（同一个联通域），如果建造才能使得花费最小？由于每个站之间的路线不同，因此造价也不一样，因此这就是一个最小生成树的实际使用场景，类似的例子还有很多。

（图来自维基百科）

不难看出，计算最小生成树就是从边集合中挑选 n - 1 个边，使得其满足生成树，并且权值和最小。

Kruskal 和 Prim 是两个经典的求最小生成树的算法，这两个算法又是如何计算最小生成树的呢？本节我们就来了解一下它们。

Kruskal

Kruskal 相对比较容易理解，推荐掌握。

Kruskal 算法也被形象地称为加边法，每前进一次都选择权重最小的边，加入到结果集。为了防止环的产生（增加环是无意义的，只要权重是正数，一定会使结果更差），我们需要检查下当前选择的边是否和已经选择的边联通了。如果联通了，是没有必要选取的，因为这会使得环产生。因此算法上，我们可使用并查集辅助完成。关于并查集，我们会在之后的进阶篇进行讲解。

下面代码中的 find_parent 部分，实际上就是并查集的核心代码，只是我们没有将其封装并使用罢了。

Kruskal 具体算法：

1. 对边按照权值从小到大进行排序。
2. 将 n 个顶点初始化为 n 个联通域
3. 按照权值从小到大选择边加入到结果集，每次贪心地选择最小边。如果当前选择的边是否和已经选择的边联通了（如果强行加就有环了），则放弃选择，否则进行选择，加入到结果集。
4. 重复 3 直到我们找到了一个联通域大小为 n 的子图

代码模板：

其中 edge 是一个数组，数组每一项都形如： (cost, fr, to)，含义是 从 fr 到 to 有一条权值为 cost 的边。

class DisjointSetUnion:
    def __init__(self, n):
        self.n = n
        self.rank = [1] * n
        self.f = list(range(n))

    def find(self, x: int) -> int:
        if self.f[x] == x:
            return x
        self.f[x] = self.find(self.f[x])
        return self.f[x]

    def unionSet(self, x: int, y: int) -> bool:
        fx, fy = self.find(x), self.find(y)
        if fx == fy:
            return False

        if self.rank[fx] < self.rank[fy]:
            fx, fy = fy, fx

        self.rank[fx] += self.rank[fy]
        self.f[fy] = fx
        return True

class Solution:
    def Kruskal(self, edges) -> int:
        n = len(points)
        dsu = DisjointSetUnion(n)

        edges.sort()

        ret, num = 0, 1
        for length, x, y in edges:
            if dsu.unionSet(x, y):
                ret += length
                num += 1
                if num == n:
                    break

        return ret

Prim

Prim 算法也被形象地称为加点法，每前进一次都选择权重最小的点，加入到结果集。形象地看就像一个不断生长的真实世界的树。

Prim 具体算法：

1. 初始化最小生成树点集 MV 为图中任意一个顶点，最小生成树边集 ME 为空。我们的目标是将 MV 填充到 和 V 一样，而边集则根据 MV 的产生自动计算。
2. 在集合 E 中 （集合 E 为原始图的边集）选取最小的边 其中 u 为 MV 中已有的元素，而 v 为 MV 中不存在的元素（像不像上面说的不断生长的真实世界的树），将 v 加入到 MV，将 加到 ME。
3. 重复 2 直到我们找到了一个联通域大小为 n 的子图

代码模板：

其中 dist 是二维数组，dist[i][j] = x 表示顶点 i 到顶点 j 有一条权值为 x 的边。

class Solution:
    def Prim(self, dist) -> int:
        n = len(dist)
        d = [float("inf")] * n # 表示各个顶点与加入最小生成树的顶点之间的最小距离.
        vis = [False] * n # 表示是否已经加入到了最小生成树里面
        d[0] = 0
        ans = 0
        for _ in range(n):
            # 寻找目前这轮的最小d
            M = float("inf")
            for i in range(n):
                if not vis[i] and d[i] < M:
                    node = i
                    M = d[i]
            vis[node] = True
            ans += M
            for i in range(n):
                if not vis[i]:
                    d[i] = min(d[i], dist[i][node])
        return ans

两种算法比较

为了后面描述方便，我们令 V 为图中的顶点数， E 为图中的边数。那么 KruKal 的算法复杂度是 $O(ElogE)$，Prim 的算法时间复杂度为 $E+VlogV$。因此 Prim 适合适用于稠密图，而 KruKal 则适合稀疏图。

大家也可以参考一下 维基百科 - 最小生成树 的资料作为补充。

另外这里有一份视频学习资料，其中的动画做的不错，大家可以作为参考，地址：https://www.bilibili.com/video/BV1Eb41177d1/

大家可以使用 LeetCode 的 1584. 连接所有点的最小费用 来练习该算法。

其他算法

A 星寻路算法

A 星寻路解决的问题是在一个二维的表格中找出任意两点的最短距离或者最短路径。常用于游戏中的 NPC 的移动计算，是一种常用启发式算法。一般这种题目都会有障碍物。除了障碍物，力扣的题目还会增加一些限制，使得题目难度增加。

这种题目一般都是力扣的困难难度。理解起来不难， 但是要完整地没有 bug 地写出来却不那么容易。

在该算法中，我们从起点开始，检查其相邻的四个方格并尝试扩展，直至找到目标。A 星寻路算法的寻路方式不止一种，感兴趣的可以自行了解一下。

公式表示为： f(n)=g(n)+h(n)。

其中：

• f(n) 是从初始状态经由状态 n 到目标状态的估计代价，
• g(n) 是在状态空间中从初始状态到状态 n 的实际代价，
• h(n) 是从状态 n 到目标状态的最佳路径的估计代价。

如果 g(n)为 0，即只计算任意顶点 n 到目标的评估函数 h(n)，而不计算起点到顶点 n 的距离，则算法转化为使用贪心策略的最良优先搜索，速度最快，但可能得不出最优解；如果 h(n)不大于顶点 n 到目标顶点的实际距离，则一定可以求出最优解，而且 h(n)越小，需要计算的节点越多，算法效率越低，常见的评估函数有——欧几里得距离、曼哈顿距离、切比雪夫距离；如果 h(n)为 0，即只需求出起点到任意顶点 n 的最短路径 g(n)，而不计算任何评估函数 h(n)，则转化为单源最短路径问题，即 Dijkstra 算法，此时需要计算最多的顶点；

这里有一个重要的概念是估价算法，一般我们使用 曼哈顿距离来进行估价，即 H(n) = D * (abs ( n.x – goal.x ) + abs ( n.y – goal.y ) )。

（图来自维基百科 https://zh.wikipedia.org/wiki/A*%E6%90%9C%E5%B0%8B%E6%BC%94%E7%AE%97%E6%B3%95 ）

有的人可能有疑问了，这到底有啥用？真有题目配得上这么高大上的解法，居然还要写代价函数才行？

还真有！有时候搜索的时候，我们无法估计搜索结束的条件，以至于会无限搜索下去。这个时候我们可以考虑使用 A * 算法。

这里有一个题目Knight-Moves-to-Target-Coordinate 就很好地体现了这一点（当前这道题可以用别的解法，但如果你用朴素的搜索，那就要用类似 A * 算法）。

这道题，什么时候算无效的状态需要重新返回呢？相比于其他题，这道题需要你自己用公式计算一个边界，这其实就对应 A * 算法的代价函数。

最后上代码。一个完整的 Python 代码模板，加了很详细的注释，因此大概改写成别的语言也不是难事。

grid = [
    [0, 1, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],  # 0 are free path whereas 1's are obstacles
    [0, 1, 0, 0, 0, 0],
    [0, 1, 0, 0, 1, 0],
    [0, 0, 0, 0, 1, 0],
]

"""
heuristic = [[9, 8, 7, 6, 5, 4],
             [8, 7, 6, 5, 4, 3],
             [7, 6, 5, 4, 3, 2],
             [6, 5, 4, 3, 2, 1],
             [5, 4, 3, 2, 1, 0]]"""

init = [0, 0]
goal = [len(grid) - 1, len(grid[0]) - 1]  # all coordinates are given in format [y,x]
cost = 1

# the cost map which pushes the path closer to the goal
heuristic = [[0 for row in range(len(grid[0]))] for col in range(len(grid))]
for i in range(len(grid)):
    for j in range(len(grid[0])):
        heuristic[i][j] = abs(i - goal[0]) + abs(j - goal[1])
        if grid[i][j] == 1:
            heuristic[i][j] = 99  # added extra penalty in the heuristic map


# the actions we can take
delta = [[-1, 0], [0, -1], [1, 0], [0, 1]]  # go up  # go left  # go down  # go right


# function to search the path
def search(grid, init, goal, cost, heuristic):

    closed = [
        [0 for col in range(len(grid[0]))] for row in range(len(grid))
    ]  # the reference grid
    closed[init[0]][init[1]] = 1
    action = [
        [0 for col in range(len(grid[0]))] for row in range(len(grid))
    ]  # the action grid

    x = init[0]
    y = init[1]
    g = 0
    f = g + heuristic[init[0]][init[0]]
    cell = [[f, g, x, y]]

    found = False  # flag that is set when search is complete
    resign = False  # flag set if we can't find expand

    while not found and not resign:
        if len(cell) == 0:
            return "FAIL"
        else:  # to choose the least costliest action so as to move closer to the goal
            # 可以用堆来存 cell 数据，效率更高
            cell.sort()
            cell.reverse()
            next = cell.pop()
            x = next[2]
            y = next[3]
            g = next[1]

            if x == goal[0] and y == goal[1]:
                found = True
            else:
                for i in range(len(delta)):  # to try out different valid actions
                    x2 = x + delta[i][0]
                    y2 = y + delta[i][1]
                    if x2 >= 0 and x2 < len(grid) and y2 >= 0 and y2 < len(grid[0]):
                        if closed[x2][y2] == 0 and grid[x2][y2] == 0:
                            g2 = g + cost
                            f2 = g2 + heuristic[x2][y2]
                            cell.append([f2, g2, x2, y2])
                            closed[x2][y2] = 1
                            action[x2][y2] = i
    invpath = []
    x = goal[0]
    y = goal[1]
    invpath.append([x, y])  # we get the reverse path from here
    while x != init[0] or y != init[1]:
        x2 = x - delta[action[x][y]][0]
        y2 = y - delta[action[x][y]][1]
        x = x2
        y = y2
        invpath.append([x, y])

    path = []
    for i in range(len(invpath)):
        path.append(invpath[len(invpath) - 1 - i])
    print("ACTION MAP")
    for i in range(len(action)):
        print(action[i])

    return path


a = search(grid, init, goal, cost, heuristic)
for i in range(len(a)):
    print(a[i])

典型题目1263. 推箱子

二分图

二分图我在这两道题中讲过了，大家看一下之后把这两道题做一下就行了。其实这两道题和一道题没啥区别。

• 0886. 可能的二分法
• 0785. 判断二分图

推荐顺序为： 先看 886 再看 785。

其他图算法

欧拉回路（一笔画）

• 332. 重新安排行程
• 法重新排列数对

Tarjan

相关知识点：桥和割点，连通分量和强连通分量

• 1192. 查找集群内的「关键连接」
• 1568. 使陆地分离的最少天数

总结

我个人将图论的学习分成了五个境界。

1. 知道图有啥用，和其他数据结构联系在哪，区别在哪。
2. 会对图进行遍历，包括 bfs 和 dfs
3. 会图的经典算法。比如 bellman A*
4. 知道这道题目该用图的哪个算法，有可能写不出来或者细节写不对。
5. 能灵活使用经典算法解决各种题目。

那么你是哪个境界？

理解图的常见概念，我们就算入门了。接下来，我们就可以做题了。

一般的图题目有两种，一种是搜索题目，一种是动态规划题目。

对于搜索类题目，我们可以：

• 第一步都是建图
• 第二步都是基于第一步的图进行遍历以寻找可行解

如果题目说明了是无环图，我们可以不使用 visited 数组，否则大多数都需要 visited 数组。当然也可以选择原地算法减少空间复杂度，具体的搜索技巧会在专题篇的搜索篇进行讨论。

图的题目相对而言比较难，尤其是代码书写层面。但是就面试题目而言， 图的题目类型却不多。

• 就搜索题目来说，很多题目都是套模板就可以解决。因此建议大家多练习模板，并自己多手敲，确保可以自己敲出来。
• 而对于动态规划题目，一个经典的例子就是Floyd-Warshall 算法，理解好了之后大家不妨拿 787. K 站中转内最便宜的航班 练习一下。当然这要求大家应该先学习动态规划，关于动态规划，我们会在后面的《动态规划》以及《背包问题》中进行深度讲解。

常见的图的板子题有以下几种：

1. 最短路。算法有 DJ 算法， floyd 算法 和 bellman 算法。这其中有的是单源算法，有的是多源算法，有的是贪心算法，有的是动态规划。
2. 拓扑排序。拓扑排序可以使用 bfs ，也可以使用 dfs。相比于最短路，这种题目属于知道了就简单的类型。
3. 最小生成树。最小生成树是这三种题型中出现频率最低的，可以最后突破。
4. A 星寻路和二分图题目比例非常低，大家可以根据自己的情况选择性掌握。

最后给大家留一个作业。图的一个很重要的问题是求最短路，这在实际应用中也非常有用。但是如果要求次短路（即除了最短路的第二短的路径）呢？力扣有一道类似的题目，大家可以作为参考 2045. 到达目的地的第二短时间