文章目录
- 人工智能
- 人工智能的诞生
- 人工智能的发展历程
- 人工智能与机器学习的关系
- 机器学习
- 机器学习的发展历程
- 讨论
- 机器学习的必要性
- 机器学习的定义
- 机器学习的三要素
- 机器学习的基本概念
- 作业
人工智能
人工智能的诞生
- 人工智能诞生于一群科学家想使用机器模拟人类思维或者人类智能的一系列问题
- 人工智能的目标是想通过计算机模拟人的某一些思维能力或者智能行为,让计算机能够像人类一样进行思考
- 人工智能应用于机器翻译、智能控制、图像理解、游戏博弈等
人工智能的发展历程
根据所使用的核心技术的不同
-
逻辑推理:主流技术是符号逻辑计算

-
知识工程:以知识工程为核心技术

-
机器学习:让机器像人类一样具有学习的能力,以机器学习为主流核心技术
起源于二十世纪五十年代的感知机数学模型
人工智能与机器学习的关系
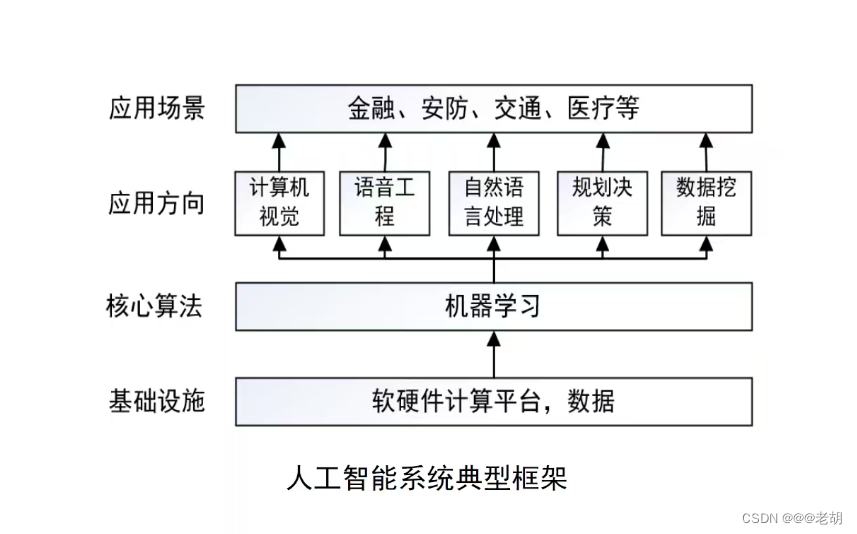
机器学习
机器学习是一种通过先验信息来提升模型能力的方式,具体说来,对于给定任务和性能度量标准,使用先验信息,通过某一种计算方式改进初始的模型,或者一个性能更好的改进模型的过程,就是机器学习。
机器学习的发展历程
-
感知机与连接学习(使用阳历信息调节神经元之间连接权重的学习方式)
通过模仿生物大脑神经网络结构的方式来实现机器智能,典型的如MP模型(无权重)、感知机(有权重、线性)
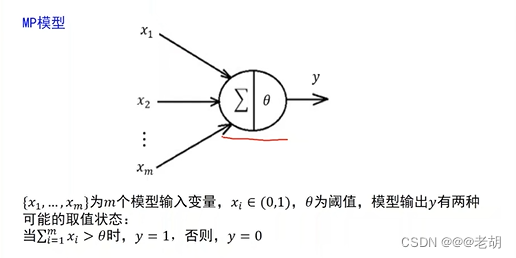
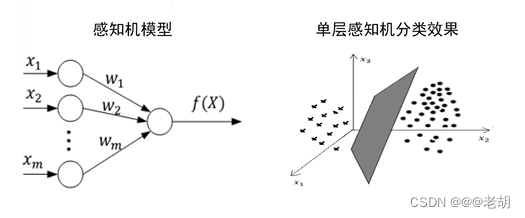
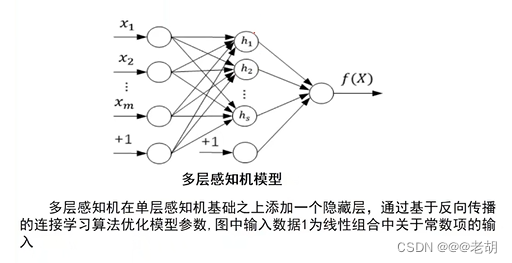
-
符号学习(逻辑推理、决策树模型)与统计学习(基于概率统计理论、支持向量机),符号学习包括:
- 记忆学习:死记硬背
- 演绎学习:从一般到特殊的学习方式
- 归纳学习:从特殊到一般的学习方式
核方法:讲低维度特征空间中线性不可分的数据映射到高维特征控件当中,使得数据在高维特征控件中线性可分,但是在计算超平面的时候还是在低维空间内,解决线性可分的问题的同时计算也比较简单。
-
连接学习的兴起——深度信念网络

-
机器学习与其他领域的关系
人工智能、表示学习、深度学习

讨论


机器学习的必要性
给出一棵树的图像,编程无法实现辨认一棵树的程序
机器学习的必要性在于:
- 系统过于复杂的,无法用编程解决的,可以使用机器学习,比如自动驾驶;
- 对于无法明确定义出一个解决方案的,可以使用机器学习,比如图像识别;
- 对于需要快速的判断和决策的,可以使用机器学学习;
- 对于需要处理非常大量的数据的,可以使用机器学习;
- 机器学习的应用非常广泛,包含了衣食住行;
- 机器学习是其他研究问题的基础,包括数据挖掘、计算机视觉、自然语言处理、生物特征识别等。
机器学习的定义
- 假设用E来评估计算机程序在某 任务类T 上的性能(度量),若一个程序通过利用经验P在T中的任务上获得了性能改善,则我们就说关于T和E,该程序对P进行了学习
- 机器学习致力研究如何通过计算的手段,利用经验来改善系统自身的性能,从而在计算机上从数据中产生“模型”,用于对新的情况给出判断

机器学习的三要素
模型+学习准则+优化算法

机器学习的实质是:根据现有的数据,寻找输入数据和输出数据的映射关系/函数,机器学习很难找到输入数据和输出数据的最佳映射关系/函数,一般来讲,只能找到符合要求的映射关系。
机器学习的基本概念
-
训练集:带有标记的数据,比如某一个瓜带有某一个特证,它的标记是好瓜,这些数据就是训练集(给出y的x的集合)
-
测试集:没有标记的数据,用来评估模型的好坏
-
标记:也即是好瓜还是坏瓜,即y
-
任务:(机器学习按照解决的问题(任务)的不同划分为以下三类)
- 回归任务:输出为连续的值,比如瓜的成熟度,甜度
- 分类任务:输出为离散值,分为二分类和多分类,比如好瓜坏瓜,非0即1
- 聚类任务:数据为无标记的数据
- 回归任务:

- 分类任务:

- 聚类任务:聚类任务的类别与分类任务不同,聚类任务的类含有特殊含义和不确定性;聚类需要设置参数,明确需要分成多少类

-
机器学习的常见类型(机器学习按照先验信息(标记、标签)的不同可以分为以下类别)
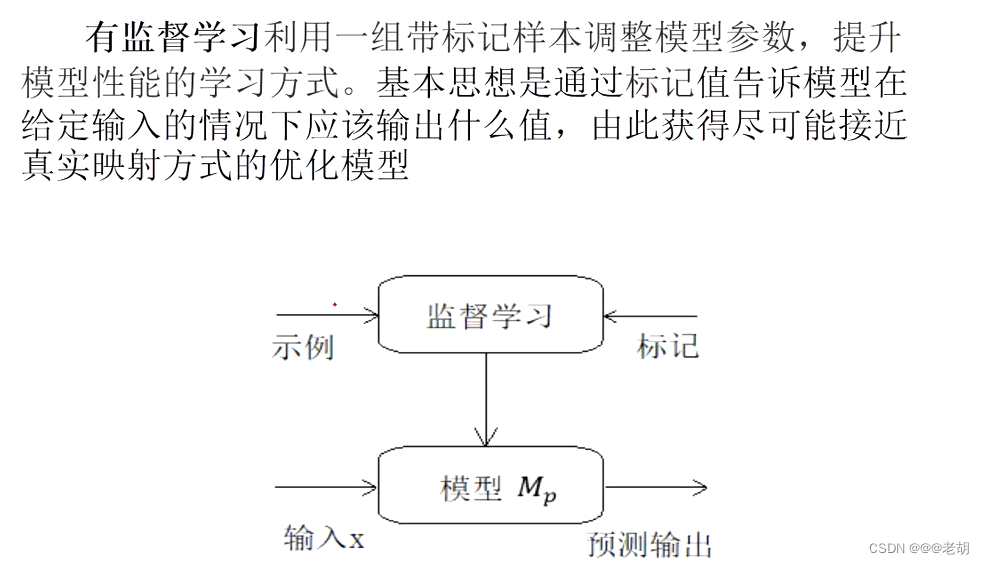
- 有监督学习:有标记的信息,包括分类和回归
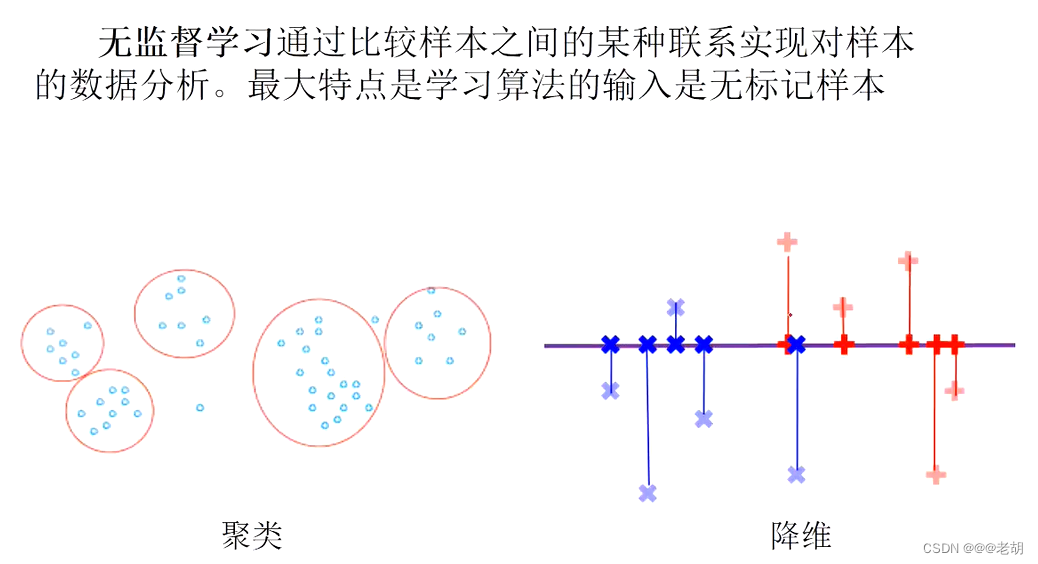
- 无监督学习:无标记信息,分为聚类和降维
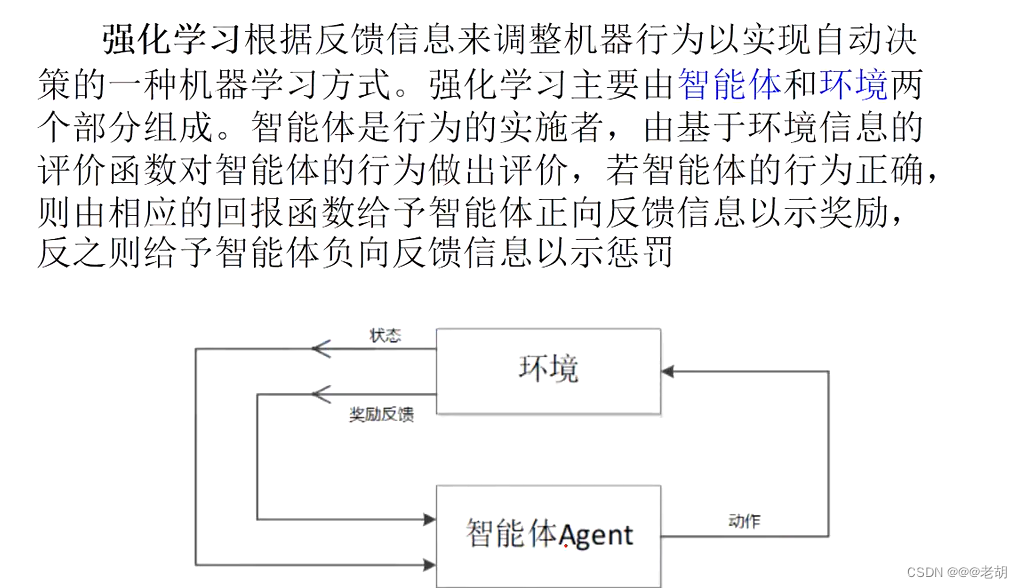
- 强化学习:环境的反馈
- 有监督学习:
- 无监督学习:
- 强化学习:不断与环境交互、通过反馈的信息来调整策略
-
泛化能力:模型适用于新样本的能力
-
假设空间:

案例说明:色泽包含了表格中的两种,还有一种其他的颜色,不包含在表格内,所以色泽有三种可能,根蒂和敲声也是同理,最终的结果映射可能映射为好瓜,也可能好瓜的概念不成立,所以需要+1
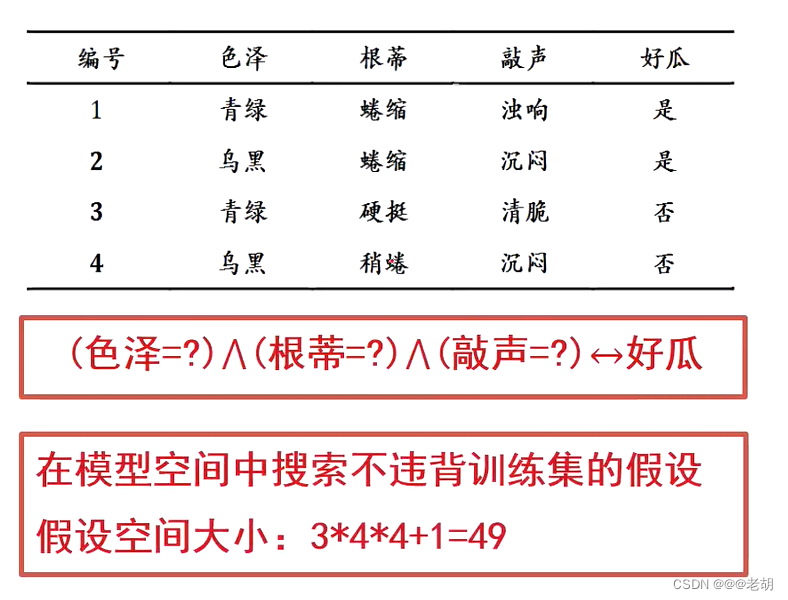
-
模型偏好:学习过程中,对某种类型结社的偏好叫做模型偏好;根据模型的偏好不同,对于预测的结果也会有所不同,如何挑选模型,要看模型泛化能力。
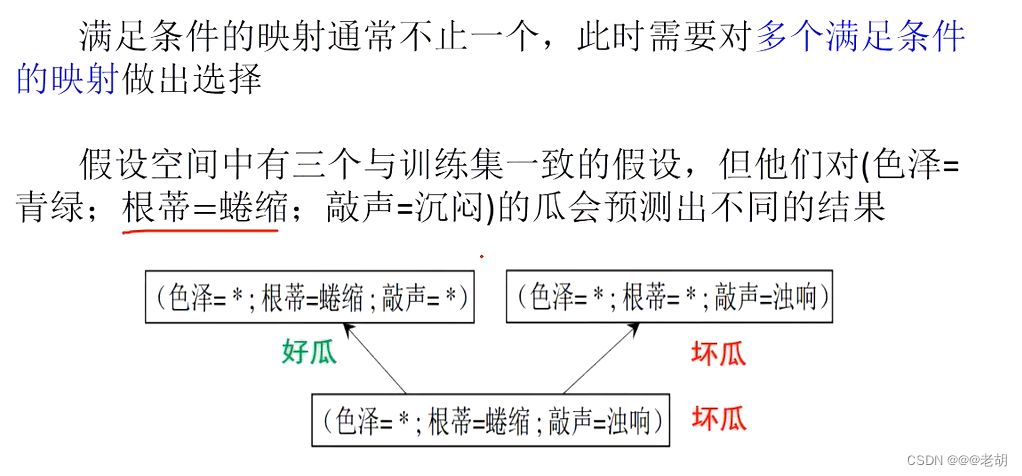
- 奥卡姆剃刀原理:如无必要,勿增实体,即简单有效原理
- 没有免费的午餐定理:

-
误差和损失函数:

- 整体误差:整体误差定义为所有单个样本所分别对应损失函数值的平均值

常见的损失函数:
0-1损失:简单但是不可导,不可以应对诸多复杂问题
平凡损失:处处可导
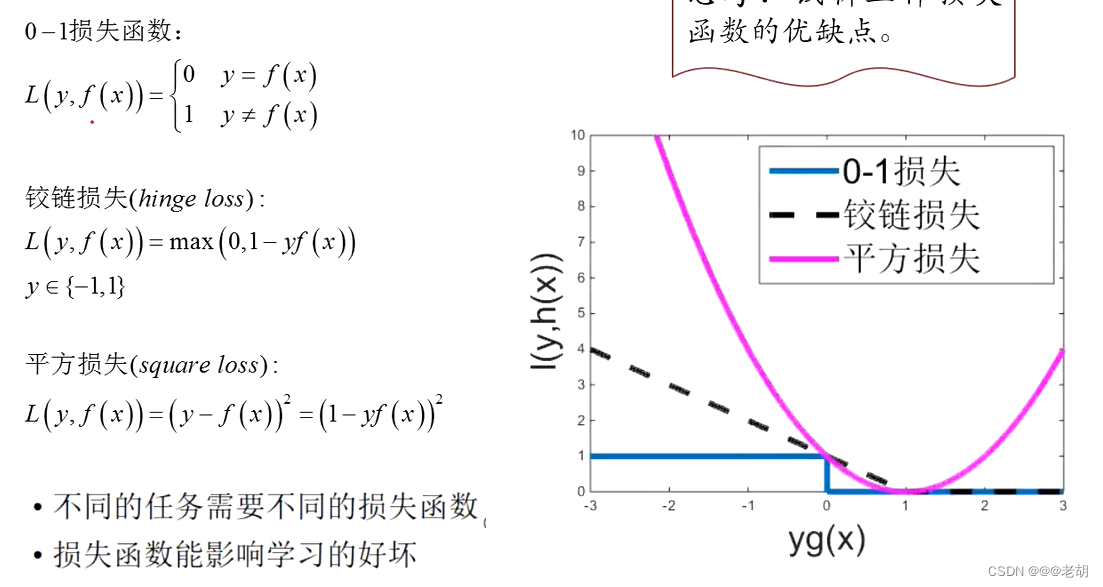
- 整体误差:整体误差定义为所有单个样本所分别对应损失函数值的平均值
-
泛化误差(期望风险)和训练误差(经验风险):

- 泛化误差(期望风险)表述的是整个样本集中的整体误差,这个很可能是达不到的,比如数据集很大、无限的时候,是达不到泛化误差的。
- 训练误差(经验风险)表述的是取一部分的样本来表达整个样本空间,在实际应用中,我们希望经验风险最小化
模型参数:根据经验风险最小化的方法得到的优化模型,即为模型参数

-
测试误差:模型在测试样本中的整体误差

-
过拟合和欠拟合
- 过拟合:同时拟合了训练样本的共性和个性特征(在学习过程中把噪声一起学进去了)
- 欠拟合:未能充分拟合训练样本的共性造成模型的泛化误差比较大,从而模型泛化能力较弱
-
偏差和方差分解


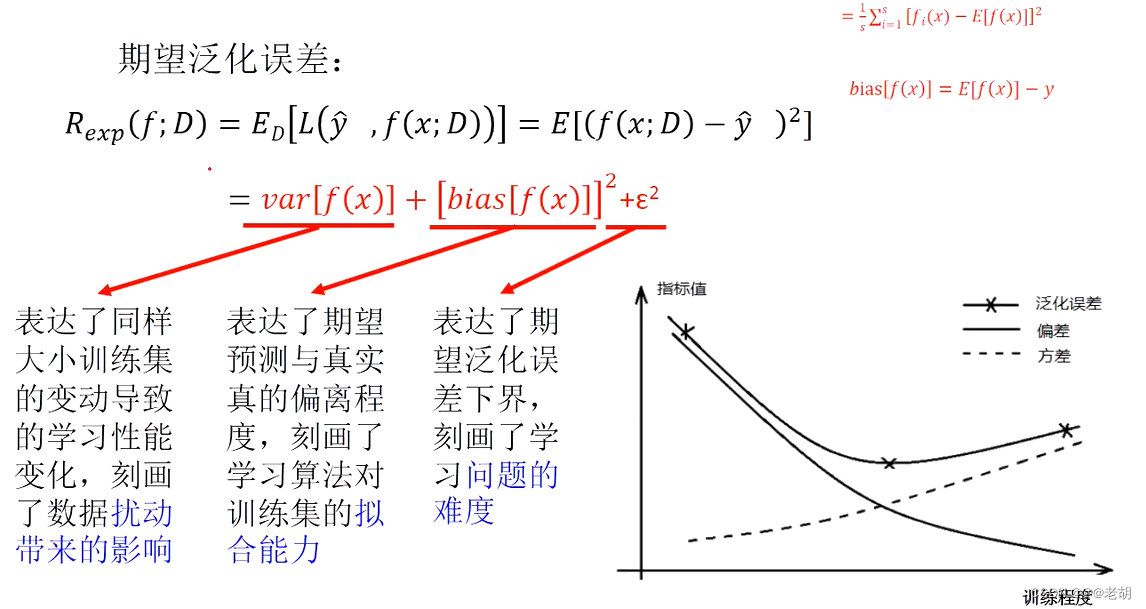
- 偏差:期望输出与真实值之间的差异
- 期望泛化误差:
y^为预测出来的结果的标记值
作业









![NSS [HNCTF 2022 WEEK2]ohmywordpress(CVE-2022-0760)](https://img-blog.csdnimg.cn/img_convert/df24d8f2dd9a6e725b96a7146a642019.png)
