前言

想要精通算法和SQL的成长之路 - 系列导航

一. 最长回文子序列

原题链接

首先，我们看下动态规划方程的定义，我们用dp[i][j] 来代表：字符串s在下标区间为[i,j]之间的最长回文子序列。

那么请问，最终的返回结果，就是我们要求得字符串s的最长回文子序列，那也就是求得dp[0][len-1]的值。那么自然而然的，我们就需要自底向上的去递归。

• 第一层循环：下标为left，范围：[0,len-1]，我们从后往前遍历。
• 第二层循环：下标为right，范围[left+1,len-1]，从前往后遍历。

试想一下，第一层为啥要从后往前遍历？我们反过来想一下，如果从左往右遍历，那么第一层的第一次循环，left就是0，那么dp[0][len-1]是不是在第二层循环的末尾就直接算出来了？此时没有走完所有的场景。

那么写成代码就是：

for (int left = len - 1; left >= 0; left--) {
    for (int right = left + 1; right < len; right++) {
    }
}

紧接着，循环的时候，递归方程怎么写？根据题目意思，我们针对left和right对应的字符串分三种情况：

• 如果s.charAt(left) == s.charAt(right)，dp[left][right] = dp[left + 1][right - 1] + 2;
  
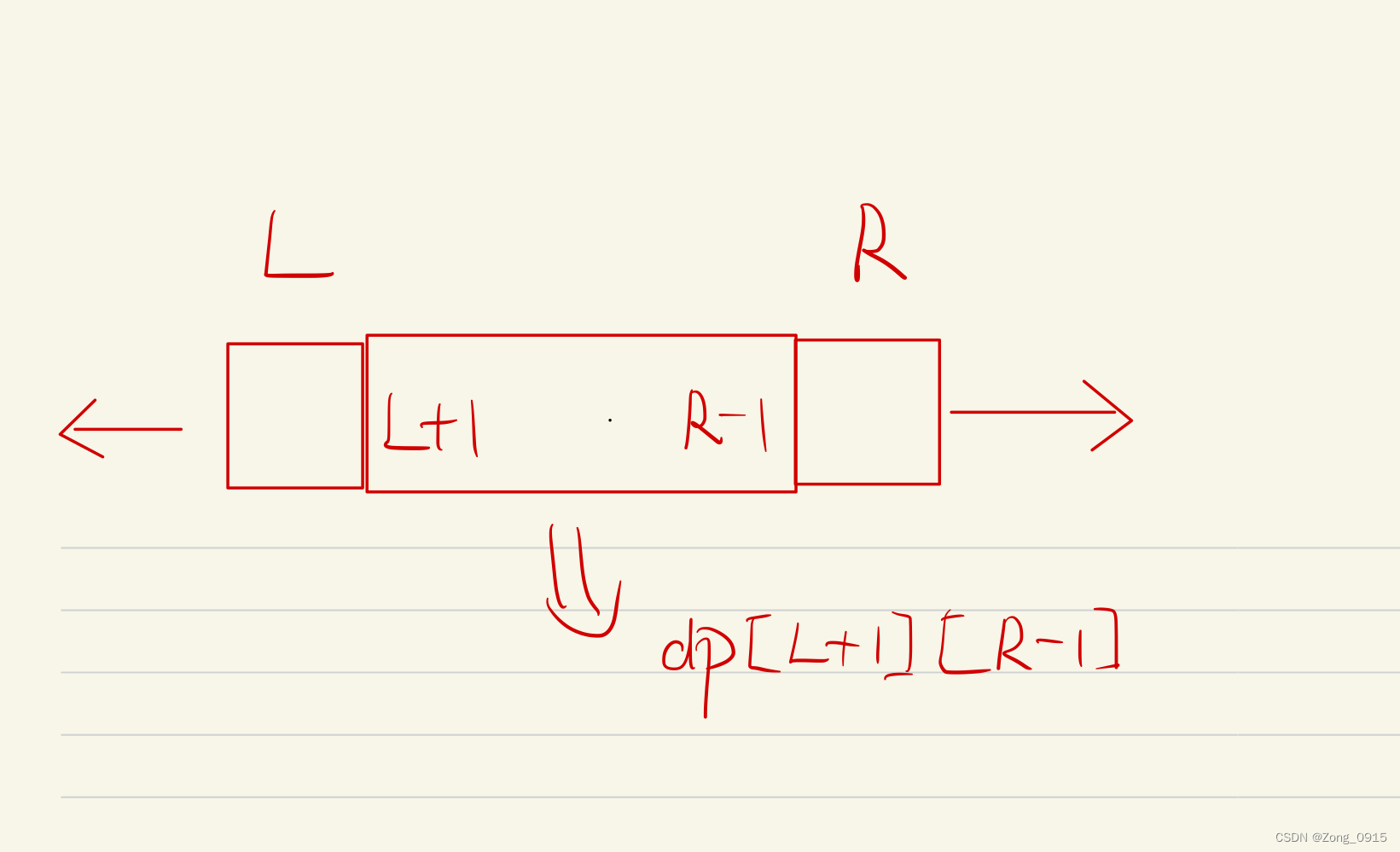
• 否则，左右两端不相等，那么此时左侧left的字符我们视为删除： dp[left][right] = dp[left + 1][right] ，要么右侧right的字符我们视为删除： dp[left][right] = dp[left][right - 1] ，两者取最大值。

因为我们的dp动态规划方程定义的是区间内的最大子序列长度，所以我们一定要做到区间的全覆盖性。我们必须选择左侧或者右侧的最近字符，并纳入计算。

最后还要注意一点的就是：回文子序列的最短长度是1，即单字符本身，我们要在每次外侧循环的时候，给个初始值。dp[left][left] = 1;

最后成代码就是：

public class Test516 {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for (int left = len - 1; left >= 0; left--) {
            dp[left][left] = 1;
            for (int right = left + 1; right < len; right++) {
                if (s.charAt(left) == s.charAt(right)) {
                    dp[left][right] = dp[left + 1][right - 1] + 2;
                } else {
                    dp[left][right] = Math.max(dp[left + 1][right], dp[left][right - 1]);
                }
            }
        }
        return dp[0][len - 1];
    }
}