1143. 最长公共子序列https://leetcode.cn/problems/longest-common-subsequence/

int longestCommonSubsequence(string text1, string text2) {

	int m = text1.size(), n = text2.size();
		
	vector<vector<int>> dp(m + 1, vector<int>(n + 1));

	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			if (text1[i] == text2[j])
			{
				dp[i + 1][j + 1] = 1 + dp[i][j];
			}
			else
			{
				dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);
			}
		}
	}

	return dp[m][n];
}

BM65 最长公共子序列(二)

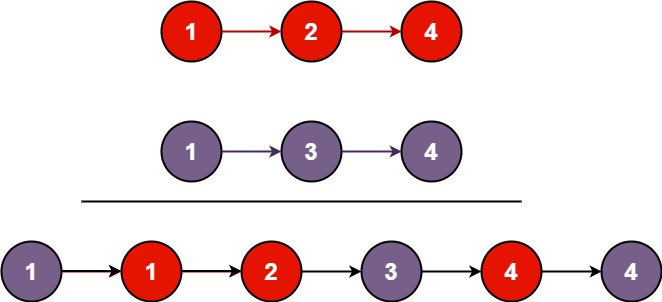
题目改成求最长公共子序列的同时、要输出这个子序列；

如果使用 vector<vector<string>> 作为dp数组的话，空间复杂度将会达到O(n三次方)；

因此这里多用一个 vector<vector<int>> 来记录最长公共子序列的遍历路径，当遍历完成后、再根据这个路径来输出结果子序列。

string LCS(string s1, string s2) {

    int m = s1.size(), n = s2.size();
    
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));
    vector<vector<pair<int, int>>> pre(m + 1, vector<pair<int, int>>(n + 1));

    for (int i = 0; i < m; ++i)
    {
        for (int j = 0; j < n; ++j)
        {
            if (s1[i] == s2[j])
            {
                dp[i + 1][j + 1] = 1 + dp[i][j];
                pre[i + 1][j + 1] = {i, j};
            }
            else
            {
                if (dp[i][j + 1] > dp[i + 1][j])
                {
                    dp[i + 1][j + 1] = dp[i][j + 1];
                    pre[i + 1][j + 1] = {i, j + 1};
                }
                else
                {
                    dp[i + 1][j + 1] = dp[i + 1][j];
                    pre[i + 1][j + 1] = {i + 1, j};
                }
            }
        }
    }

    if (dp[m][n] == 0)
    {
        return "-1";
    }

    string res;
    int i = m, j = n;
    while (i != 0 && j != 0)
    {
        if (s1[i - 1] == s2[j - 1])
        {
            res = s1[i - 1] + res;
        }
        
        pair<int, int> temp = pre[i][j];
        i = temp.first;
        j = temp.second;
    }

    return res;
}

 坑：

最后的

pair<int, int> temp = pre[i][j];
i = temp.first;
j = temp.second;

不能写成

i = pre[i][j].first;

j = pre[i][j].second;        // 此时 i 已被改变