6.1 间隔与支持向量

6.1.1 什么是支持向量机

支持向量机（Support Vector Machine，SVM）是一种广泛应用于模式分类和回归分析的机器学习算法。它在数据分析和模式识别领域有着重要的应用，特别是在小样本、高维数据以及非线性数据分析方面表现出色。

SVM 的 基本思想是通过在特征空间中寻找一个能够最大化分类间距的超平面来进行分类。 在二分类问题中，SVM试图找到一个能够将两个类别的数据点尽可能分开的超平面。这个超平面可以被看作是一个“决策边界”，将不同类别的数据点分隔开来。SVM的目标是找到这个超平面，使得其到最近的数据点的距离（即支持向量）最大化，从而提高分类的鲁棒性和泛化能力。

SVM还可以通过核函数来处理非线性分类问题。核函数能够将原始的特征映射到更高维的空间中，从而使数据在新的空间中线性可分。这使得SVM能够处理复杂的非线性关系。

SVM的主要优点包括：

• 高效处理高维数据：SVM适用于高维特征空间中的数据，且在处理小样本问题时表现出色。
• 泛化能力强：SVM在训练过程中通过最大化支持向量间的间隔，能够产生具有较好泛化能力的模型。
• 可处理非线性问题：通过核函数，SVM能够处理复杂的非线性分类问题。

需要注意的是，

• SVM在处理大规模数据时可能会变得复杂和耗时；
• 在选择合适的核函数和参数时，需要进行调参来获得最佳的性能。
  

6.1.2 支持向量与间隔

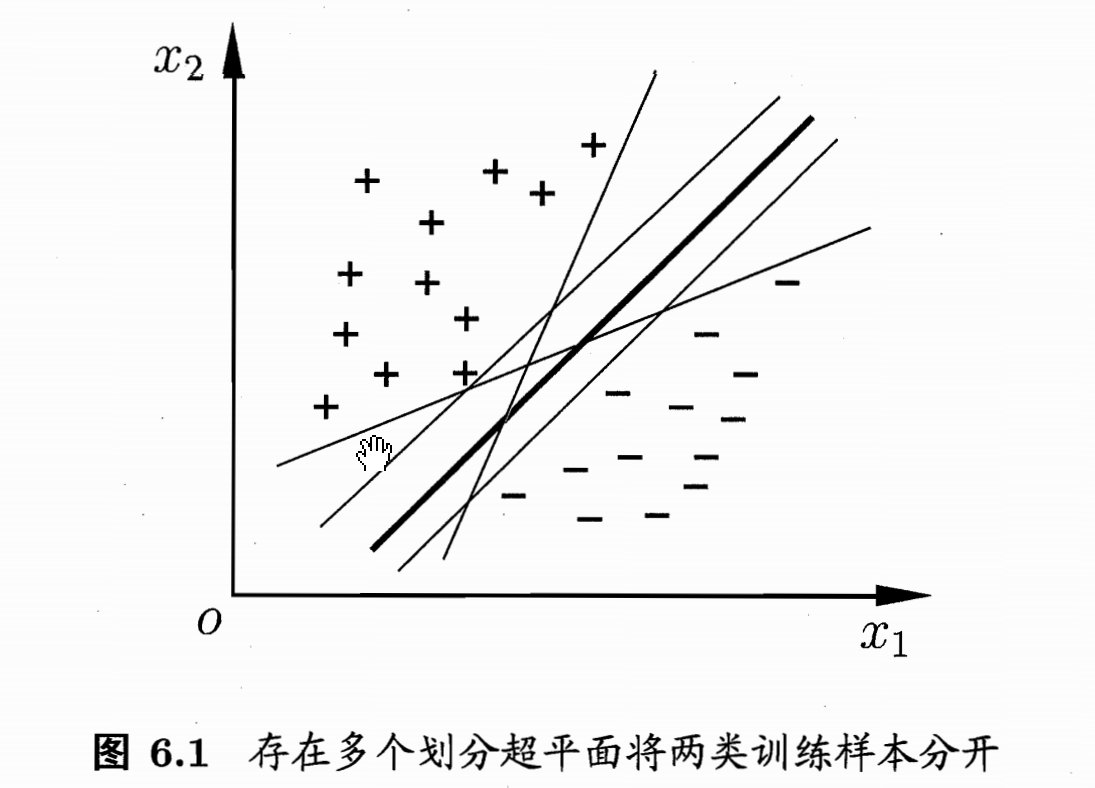
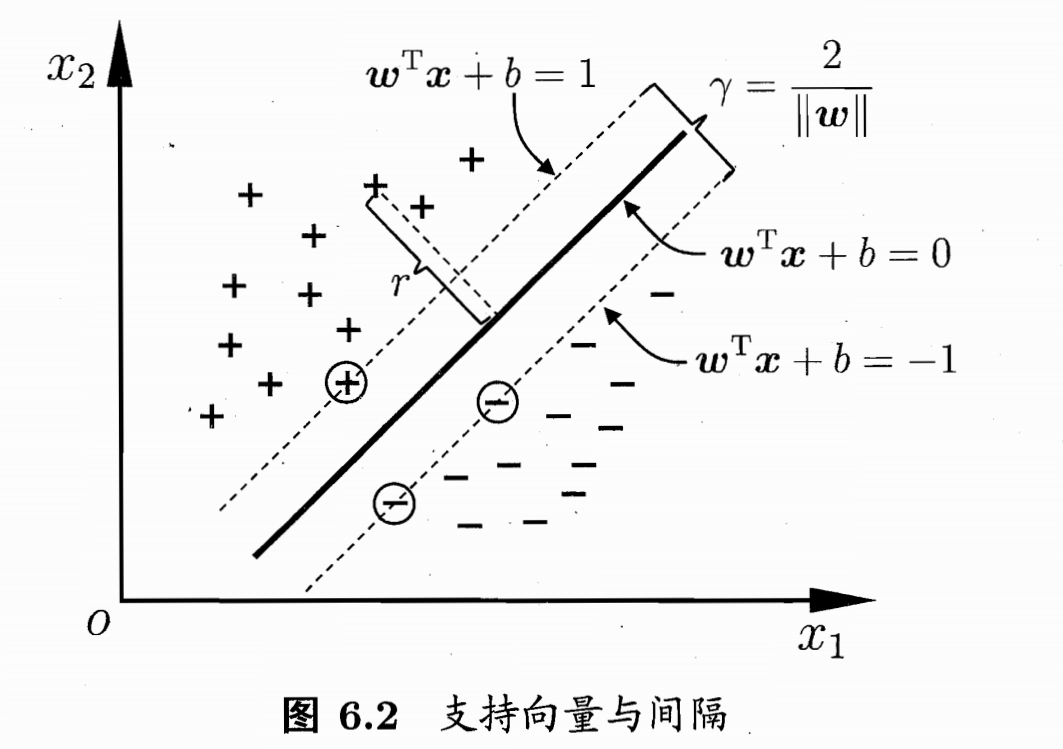
前面曾提过 SVM 的 基本思想是通过在特征空间中寻找一个能够最大化分类间距的超平面来进行分类，如下图所示，中间加粗的线（实体书中红色的线）即是寻找所得的超平面，距离超平面最近的这几个训练样本点构成 “支持向量（support vector）”，两个异类支持向量到超平面的距离之和 称为 “间隔（margin）”。

6.1.3 支持向量机的求解过程

支持向量机（Support Vector Machine，SVM）是一种常用于分类和回归任务的机器学习算法。它的目标是找到一个超平面（在二维空间中即为一条直线，在多维空间中为一个超平面），将不同类别的样本分开，并且使得两侧距离最近的样本点到该超平面的距离最大化。这些最近的样本点被称为支持向量。

以下是支持向量机的求解过程概述：

1. 数据准备： 首先，你需要准备带有标签的训练数据集，其中每个样本都有一个特征向量和对应的类别标签。

2. 选择核函数： 核函数是SVM中的一个重要概念，它允许将数据从原始特征空间映射到一个更高维的空间，从而使得数据更容易分割。常用的核函数有线性核、多项式核和径向基函数（RBF）核等。

3. 优化问题建立： SVM的目标是求解一个最优化问题，该问题的形式取决于具体的SVM类型。在标准的线性SVM中，目标是找到一个最大间隔的超平面，可以用以下形式表示：

   最小化： $\frac{1}{2}||w|{|}^2$

   约束条件： $y_i(w\cdot x_i+b)\ge 1$，对所有的训练样本 $(x_i,y_i)$，其中 $y_i$ 是样本的类别标签（+1 或 -1）。

   在这里，$w$ 是超平面的法向量，$b$ 是偏置项。

4. 求解优化问题： 优化问题可以使用不同的优化算法来求解，常见的有梯度下降法、坐标下降法等。优化的目标是找到合适的 $w$ 和 $b$，使得目标函数最小化，并满足约束条件。

5. 支持向量的确定： 在求解过程中，部分样本点会成为支持向量，即最靠近超平面的样本点。这些样本点对于确定超平面起到关键作用。

6. 分类和预测： 一旦得到了最优的超平面，你可以使用该超平面对新的未标记样本进行分类预测。对于线性核，分类决策可以通过计算 $w\cdot x+b$ 的符号来实现。

上述步骤描述了标准的线性SVM的求解过程。如果使用非线性核函数，比如RBF核，那么数据会被映射到更高维的特征空间，在这个空间中寻找最优超平面。非线性SVM的求解过程类似，但涉及到核函数的计算。

总之，支持向量机是一个强大的分类和回归算法，其核心思想是找到一个最大间隔的超平面，以有效地对不同类别的数据进行分类。

6.2 对偶问题（dual problem）

6.2.1 什么是对偶问题

为了最大化间隔，仅需最大化 $||w|{|}^{-1}$，这等价于最小化 $||w|{|}^2$ ，即

$$\begin{array}{ll}{\min }_{\mathbf{w},b}& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ & \\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m.\end{array}\text{\hspace{1em}(6.6)}$$

对式 (6.6) 使用拉格朗日乘子法可得到其 “对偶问题”，具体来说，对式(6.6)的每条约束添加拉格朗日乘子 ${\alpha }_i\ge 0$ ，则该问题的拉格朗日函数可写为

$$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\right)\text{\hspace{1em}(6.8)}$$

其中 $\alpha =({\alpha }_1;{\alpha }_2;...;{\alpha }_m)$。令 $L(\mathbf{w},b,\mathbf{\alpha })$ 对 $\omega$ 和 $b$ 的偏导为零可得

$$\mathbf{w}=\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i\text{\hspace{1em}(6.9)}$$

$$0=\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(6.10)}$$

将式(6.9)代入 (6.8)，即可将 $L(\mathbf{w},b,\mathbf{\alpha })$ 中的 $\mathbf{w}$ 和 $b$ 消去，再考虑式(6.10) 的约束，就得到式（6.6）的对偶问题

$$\begin{gathered} \underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j \\ \begin{array}{ll}& \\ & \\ \text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ & \\ & \\ & {\alpha }_i⩾0,i=1,2,\dots ,m.\end{array}\text{\hspace{1em}(6.11)} \end{gathered}$$

解出 $\mathbf{\alpha }$，求出 $\mathbf{w}$ 与 $b$ 即可得到模型

$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i^{\mathrm{T}}\mathbf{x}+b.\end{array}\text{\hspace{1em}(6.12)}$$

从对偶问题（6.11）求解出的 ${\alpha }_i$ 是式 (6.8) 中的拉格朗日乘子，它恰对应着训练样本（${\mathbf{x}}_i,y_i$）。注意到式（6.6）中有不等式约束，因此上述过程需满足 $\text{KKT}$ （Karush-Kuhn-Tucker）条件，即要求

$$\{\begin{array}{l}{\alpha }_i⩾0\\ y_{i}f\left({\mathbf{x}}_i\right)-1⩾0\\ {\alpha }_i\left(y_{i}f\left({\mathbf{x}}_i\right)-1\right)=0.\end{array}\text{\hspace{1em}(6.13)}$$

6.2.2 如何求解支持向量机的对偶问题

支持向量机（Support Vector Machine，SVM）的对偶问题 是通过对原始优化问题进行转化得到的一个等价问题。解决对偶问题可以带来一些优势，例如在使用核函数进行非线性分类时更加方便。下面我将简要介绍支持向量机的对偶问题。

原始的支持向量机问题是一个凸二次规划问题，如前面提到的目标函数最小化：

最小化： $\frac{1}{2}||w|{|}^2$

约束条件： $y_i(w\cdot x_i+b)\ge 1$，对所有的训练样本 $(x_i,y_i)$。

支持向量机的对偶问题则是基于拉格朗日对偶性（Lagrange Duality）得到的。拉格朗日对偶性是优化问题理论中的一个重要概念，它允许将原始问题转化为一个对偶问题，从而更好地处理一些复杂的优化问题。

对于支持向量机，对偶问题的形式如下：

最大化： ${\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j$

约束条件： ${\sum }_{i=1}^N{\alpha }_i{y}_i=0$

其中，${\alpha }_i$ 是拉格朗日乘子，对应于每个训练样本的约束条件。解决这个对偶问题会得到一组拉格朗日乘子的值，然后可以使用这些乘子计算出权重向量 $w$ 和偏置项 $b$，进而实现分类。

对偶问题的一个重要性质是，只有支持向量对应的拉格朗日乘子 ${\alpha }_i$ 不为零，其他非支持向量的乘子都为零。这意味着只有支持向量对最终的分类超平面有影响，这也是支持向量机名称的由来。

总之，支持向量机的对偶问题是通过拉格朗日对偶性将原始问题转化得到的，通过解决对偶问题可以更好地理解支持向量机算法，尤其在使用核函数处理非线性问题时更为便捷。

6.3 核函数（kernel function）

6.3.1 什么是支持向量机的核函数

核函数 是支持向量机通过某非线性变换将输入空间映射到高维特征空间，以实现数据分类或回归的目的。

$$\mathbf{K}=\left[\begin{array}{ccccc}\kappa \left({\mathbf{x}}_1,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_1,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_1,{\mathbf{x}}_m\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_m\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_m\right)\end{array}\right]$$

具体的求解过程请参照原书籍或相关资料。

6.3.2 常见的几种核函数

名称	表达式	参数
线性核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$
多项式核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\right)}^d$	$d\ge 1$ 为多项式的次数
高斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{||{\mathbf{x}}_i-{\mathbf{x}}_j|{|}^2}{2{\sigma }^2}\right)$	$\sigma >0$ 为高斯核的带宽（width）
拉普拉斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{||{\mathbf{x}}_i-{\mathbf{x}}_j||}{\sigma }\right)$	$\sigma$ > 0
Sigmoid 核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\tanh \left(\beta {\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j+\theta \right)$	tanh 为双曲正切函数，$\beta >0,\theta <0$

6.4 软间隔（soft margin）与正则化（regularization）

软间隔是支持向量机的一个概念，用于处理在数据中存在一些噪声或异常值的情况。

软间隔的主要思想是在最大化间隔（超平面到支持向量的距离）的同时，引入一个松弛因子（slack variable）来容忍一些分类错误。这个松弛因子可以通过调整模型的超参数来控制，通常由正则化参数 $C$ 来表示。较小的 $C$ 值会放宽软间隔，允许更多的分类错误，而较大的$C$ 值会加强间隔，更强调减小分类错误。这样，通过调整 $C$ 的值，可以在模型的偏差和方差之间找到一个平衡点，以满足实际数据的特性。

6.5 支持向量回归（Support Vector Regression, SVR）

支持向量机回归（Support Vector Machine Regression，SVM回归）是一种用于解决回归问题的机器学习算法，与支持向量机分类（SVM分类）类似，但其目标是拟合数据并预测连续数值输出，而不是离散的类别。

SVM回归的基本思想是寻找一个超平面（在特征空间中的线性函数），以最佳方式拟合训练数据的分布，同时尽量使数据点落在超平面周围的间隔带（或者说支持向量）内。与SVM分类不同，SVM回归的目标是最小化模型的预测误差，而不是最大化间隔。

SVM回归可以处理线性回归和非线性回归问题，通过使用核函数来处理非线性关系。与传统的线性回归方法相比，SVM回归在处理异常值和噪声方面通常更具鲁棒性，并且可以适应复杂的数据分布。然而，选择适当的超参数和核函数仍然是一个重要的挑战。

6.6 核方法

支持向量机（Support Vector Machine，SVM）的核方法是一种用于处理非线性分类和回归问题的重要技术。核方法允许SVM在原始特征空间中无法线性分隔的数据集上进行高效的非线性建模。核方法的核心思想是将数据映射到一个高维特征空间，使得在这个特征空间中数据更容易线性分隔。这个映射通常通过一个称为核函数（Kernel Function）的数学函数来实现。核函数的相关内容在 6.1.3 节中已经介绍。核函数直接决定了支持向量机的最终性能，但遗憾的是，核函数的选择是一个未解决问题。

核方法的关键优势在于，它们能够在高维特征空间中有效地进行计算，而无需显式计算映射后的特征向量，从而节省了计算成本。这使得SVM可以处理非常大的数据集和复杂的非线性问题。

在使用SVM时，选择合适的核函数和核函数参数是至关重要的，因为它们会直接影响模型的性能。通常需要通过交叉验证等技术来调整这些超参数，以获得最佳的模型性能。

6.7 其他问题

节选部分课本上对应的习题

6.7.1 SVM对噪声敏感的原因

支持向量机（Support Vector Machine，SVM）在某些情况下对噪声敏感的原因可以归结为以下几个方面：

• 间隔带的影响：SVM在训练时会尽量找到一个能够将正负样本分开的超平面，并确保在这个超平面周围有一个较大的间隔带（Margin）。噪声数据点可能位于间隔带内部，而SVM为了最大化间隔带，会对这些噪声数据点产生较大的敏感性，导致分类边界的波动。

• 硬间隔与软间隔：SVM有硬间隔（Hard Margin）和软间隔（Soft Margin）两种形式。硬间隔要求所有训练数据点都正确分类且间隔带为最大，这在存在噪声的情况下可能导致模型过于复杂，容易过拟合噪声。软间隔则允许一定数量的数据点落在间隔带内部，但在存在噪声时，模型可能会过于容忍噪声而导致性能下降。

• 异常值的影响：噪声数据通常被视为异常值，它们可能远离其他数据点，导致SVM在寻找超平面时过于受到这些异常值的影响。SVM试图最小化误分类的样本数量，因此会努力将异常值正确分类，这可能导致边界的扭曲和性能下降。

• 数据不平衡：如果数据集中的噪声占据了较大比例，那么SVM可能会偏向于学习噪声而忽略真正的信号。这在数据不平衡的情况下尤为明显，因为噪声数据点数量多于真正的样本。

6.8 总结

支持向量机应该也是面试时提问重灾区，很多事情总是会有 “似懂非懂” 之感。

共勉 。

Smileyan
2023.09.17 16:27