Floyd算法-最短路径问题

算法结束

Floyd算法：求出每一对顶点之间的最短路径

核心：使用动态规划思想，将问题的求解分为多个阶段：

对于n个顶点的图G，求任意一对顶点V_i->V_j之间的最短路径可分为如下几个阶段：

• 初始：不允许在其他顶点中转，最短路径是？
• 0：若允许在$V_0$中转，最短路径是？
• 1：若允许在$V_0,V_1$中转，最短路径是？
• 2：若允许在$V_0，V_1，V_2$中转，最短路径是？
• …
• n-1：若允许在$V_0，V_1，V_2，V_{n-1}$中转，最短路径是？

算法思想

如果不涉及到写代码的话，这里推荐观看Floyd算法求最短路径最简易方法！几分钟学会_哔哩哔哩_bilibili，绝对的快

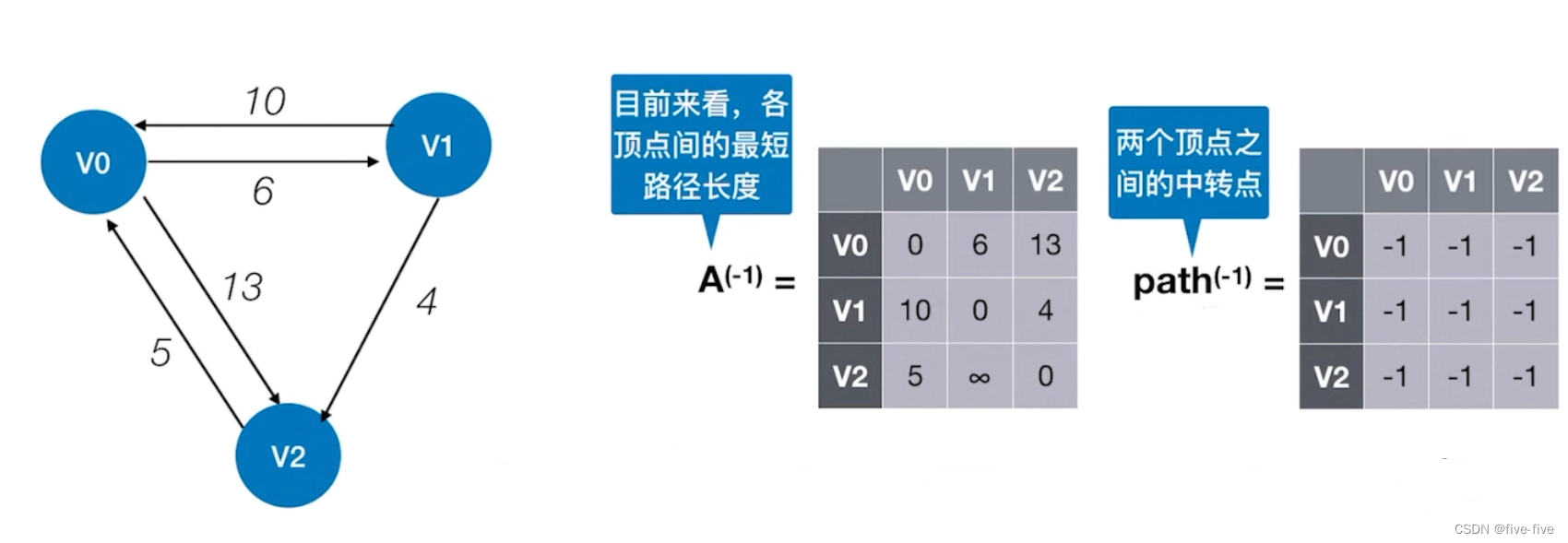
//...准备工作，根据图的信息初始化矩阵A和path(如上图)
for(int k=0;k<n;k++){//考虑以Vk作为中转点
	for(int i=0;i<n;i++){//遍历整个矩阵，i为行号，j为列号
		for(int j=0;j<n;j++){
			if(A[i][j]>A[i][k]+A[k][j]){//以Vk为中转点的路径最短
				A[i][j]=A[i][k]+A[k][j];//更新最短路径长度
				path[i][j]=k;//中转点
			}
		}
	}
}

算法效率分析

1. 时间复杂度：$O({|V|}^3)$
2. 空间复杂度：$O(|V{|}^2)$

Floyd算法无法解决带有“负权回路”的图(有负权值的边组成回路)，这种图有可能没有最短路径

‍