题目大意

给你一个链表，要求判断是否有环，若有环，找出环的入口结点。

142. 环形链表 II

判断是否有环

判环比较简单，用一个一次走一个结点的快指针，和一个一次走一个结点的慢指针同时遍历链表，若两指针相遇则链表有环，若两指针有一遇到NULL则无环。重点在于如何找到环的入口结点。

找环的入口结点

解法一：Hash+遍历

用一个指针遍历链表，将经过的所有结点都加入hashmap中，遇到重复的结点即为有环，且环入口结点就是该重复结点。代码略。

解法二：快慢指针

快慢指针的解法相同，但是推导或者说证明的思路会有差异。

思路一

代码随想录里的思路，也是常规证明思路，视频讲解：链表：6.环形链表||

思路二

我自己的推导思路，相对比较直观，但是过程比较繁琐。

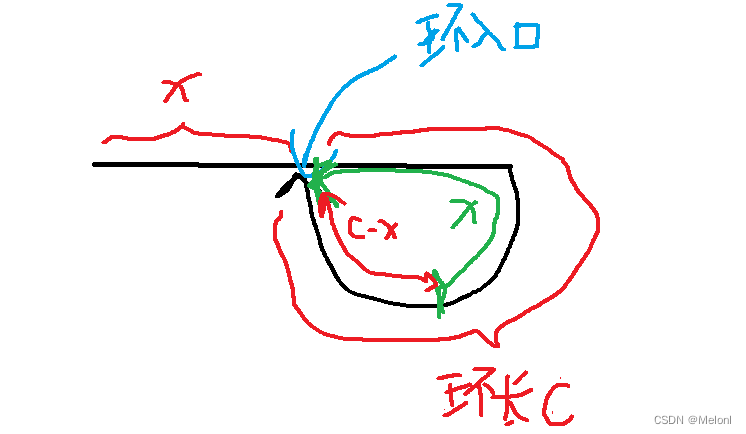
设链表头结点到环入口结点的距离为x，环周长为c，快指针f，慢指针s，f一次走两个结点，s一次走一个结点。

此处我参考了直线匀速运动的追及问题。当快指针f到达环入口结点时，f刚好走了长度为x的路程，而s刚好在x/2处（f的速度是s的两倍），记此时刻为时刻一；

当s到达环入口结点时，s相对于时刻一继续走了x/2，而f则是相对于时刻一在环上走了x的路程，注意，此处x可能大于环长，即f可能此时可能已经在环上走了n圈s才刚到达环入口，记此时刻为时刻二；

在时刻二，s在环入口，f在环上走了x（要是c小于x怎么办？也即f在环上绕了很多圈的情况，其实并不影响，因为这个x始终说的都是追及距离，也就是f追上s要往前走的距离，毕竟f不可能倒退），即f此时在环上还没有走满一圈，那么此时f还要走 c-x 才能到达环的入口，也即此时f与s的距离为c-x（追及距离，即只考虑f往前走），类比匀速直线运动的追及问题，f的速度是s的两倍，可以推出在时刻二后，f追上s时，s在环上恰好走了c-x，记此时刻为时刻三，时刻三即为f与s相遇的时刻。

在时刻三，s与f相遇，此时相比时刻二，s在环上走了c-x，那么s还要继续往前走 c-(c-x)，即x， 才能走满一圈重新到达环的入口，也就是说，到此可以推导出：f与s第一次相遇的点y，到环入口结点的距离（追及距离，只考虑指针往前走的距离）为x。

那么，接下来只要我们用一个指针指向相遇点y，一个指针指向链表头结点，将两个指针同时往前移动，当两指针相遇时，即找到环的入口结点。

证明过程中分的时刻一二三只是为了稍微严谨一些，实际上如果读者跟着文字用纸画出来理解的话这个思路很简单易懂，这个思路有一个很重要的参考是直线匀速运动的追及问题：当a的速度为b的两倍时，若a在b后方c米处，二人同时起跑，则最终b会在距离a起点处2c的距离被a追上，也即b会在跑了c米时被追上。

代码

    ListNode *detectCycle(ListNode *head) {
        if(head == NULL || head->next == NULL)return NULL;

        ListNode*f = head, *s = head;
        ListNode* met = NULL;  //指向相遇结点
        while(f && f->next){
            f = f->next->next;
            s = s->next;
            if(s == f){
                met = s;
                break;
            }
        }
        //无环
        if(met == NULL)return NULL;

        //找环入口
        s = head;
        while(s != met){
            s = s->next;
            met = met->next;
        }
        return s;
    }