目录
前言
坐标变换引起法向量变化
变化规律:
魔法矩阵:逆转置矩阵
逆转置矩阵的用法总结
Matrix4对象的 setInverseOf 、transpose 方法规范(以完成逆转置矩阵)
示例代码(LightedTranslatedRotatedCube.js)
代码详解
示例效果
前言
场景中的物体运动,观察者的视角也很可能会改变,物体平移、缩放、旋转都可以用坐标变换来表示。显然,物体的运动会改变每个表面的法向量,从而导致光照效果发生变化。下面就来研究如何实现这一点。
在本次程序LightedTranslatedRotatedCube中,立方体先绕z轴顺时针旋转了90度,然后沿着y轴平移了0.9个单位。场景中的光照情况与前面的 WebGL光照介绍——平行光、环境光下的漫反射_山楂树の的博客-CSDN博客 LightedCube_ambient一样,即有平行光又有环境光。程序运行的效果如下所示。

坐标变换引起法向量变化
立方体旋转时,每个表面的法向量也会随之变化。在下图中,我们沿着z轴负方向观察一个立方体,最左边是立方体的初始状态,图中标出了立方体右侧面的法向量(1,0,0),它指向x轴正方向,然后对该立方体进行变换,观察右侧面法向量随之变化的情况。
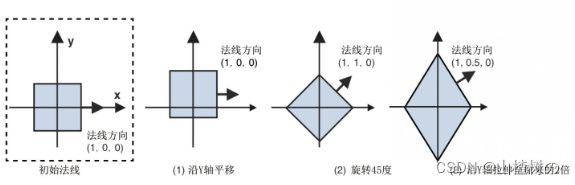
变化规律:
● 平移变换不会改变法向量,因为平移不会改变物体的方向。
● 旋转变换会改变法向量,因为旋转改变了物体的方向。
● 缩放变换对法向量的影响较为复杂。如你所见,最右侧的图显示了立方体先旋转了45度,再在y轴上拉伸至原来的2倍的情况。此时法向量改变了,因为表面的朝向改变了。但是,如果缩放比例在所有的轴上都一致的话,那么法向量就不会变化。最后,即使物体在某些轴上的缩放比例并不一致,法向量也并不一定会变化,比如将最左侧图中的立方体在y轴方向上拉伸两倍,法向量就不会变化。
显然,在对物体进行不同变换时,法向量的变化情况较为复杂(特别是缩放变换时)。这时候,数学公式就会派上用场了。
魔法矩阵:逆转置矩阵
曾讨论过,对顶点进行变换的矩阵称为模型矩阵。如何计算变换之后的法向量呢?只要将变换之前的法向量乘以模型矩阵的逆转置矩阵(inverse transpose matrix)即可。所谓逆转置矩阵,就是逆矩阵的转置。
逆矩阵的含义是,如果矩阵M的逆矩阵是R,那么R*M或M*R的结果都是单位矩阵。转置的意思是,将矩阵的行列进行调换(看上去就像是沿着左上-右下对角线进行了翻转)。
逆转置矩阵的用法总结
规则:用法向量乘以模型矩阵的逆转置矩阵,就可以求得变换后的法向量。
求逆转值矩阵的两个步骤:
1.求原矩阵的逆矩阵。
2.将上一步求得的逆矩阵进行转置。
Matrix4对象 WebGL矩阵变换库_山楂树の的博客-CSDN博客 提供了便捷的方法来完成上述任务,如下所示。
Matrix4对象的 setInverseOf 、transpose 方法规范(以完成逆转置矩阵)

假如模型矩阵存储在modelMatrix对象(Matrix4类型的实例)中,那么下面这段代码将会计算它的逆转值矩阵,并将其存储在normalMatrix对象中(将其命名为normalMatrix是因为它被用来变换法向量):

下面来看看示例程序LightedTranslatedRotatedCube.js的代码。该程序使立方体绕z轴顺时针旋转90度,然后沿y轴平移0.9个单位,并且处于平行光和环境光的照射下。立方体在变换之前,与WebGL光照介绍——平行光、环境光下的漫反射_山楂树の的博客-CSDN博客LightedCube_ambient中的立方体完全相同。
示例代码(LightedTranslatedRotatedCube.js)
如下显示了示例程序的代码。与WebGL光照介绍——平行光、环境光下的漫反射_山楂树の的博客-CSDN博客LightedCube_ambient相比,顶点着色器新增了u_NormalMatrix矩阵(第6行)用来对顶点的法向量进行变换(第14行)。你需要事先在JavaScript中计算出该变量,再将其传入着色器。
var VSHADER_SOURCE = // p301
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'attribute vec4 a_Normal;\n' +
'uniform mat4 u_MvpMatrix;\n' +
'uniform mat4 u_NormalMatrix;\n' + // 用来变换法向量的矩阵
'uniform vec3 u_LightColor;\n' + // 平行光颜色
'uniform vec3 u_LightDirection;\n' + // 光线方向归一化的世界坐标
'uniform vec3 u_AmbientLight;\n' + // 环境光颜色
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_MvpMatrix * a_Position;\n' +
// 计算变换后的法向量并归一
' vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
// 计算光线方向和法向量的点积(即两者归一化后的夹角的余弦值:cosθ)
' float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
// 计算漫反射光的颜色(入射光颜色 * 表面基底色 * cosθ)
' vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
// 计算环境光产生的反射光的颜色
' vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
// 将以上两者相加作为最终的颜色(物体表面的反射光颜色 = 漫反射光颜色 + 环境反射光颜色)
' v_Color = vec4(diffuse + ambient, a_Color.a);\n' +
'}\n';
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' +
'#endif\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_FragColor = v_Color;\n' +
'}\n';
function main() {
var canvas = document.getElementById('webgl');
var gl = getWebGLContext(canvas);
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) return
var n = initVertexBuffers(gl);
gl.clearColor(0, 0, 0, 1);
gl.enable(gl.DEPTH_TEST);
// 获取uniform等变量的存储地址
var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
// 设置平行光为白色
gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
// 设置光线方向
var lightDirection = new Vector3([0.0, 3.0, 4.0]);
lightDirection.normalize(); // 归一
gl.uniform3fv(u_LightDirection, lightDirection.elements);
// 设置环境光颜色
gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);
var modelMatrix = new Matrix4(); // 视图矩阵
var mvpMatrix = new Matrix4(); // 模型视图投影矩阵
var normalMatrix = new Matrix4(); // 用来变换法向量的逆转置矩阵
// 计算模型矩阵
modelMatrix.setTranslate(0, 0.9, 0); // 沿Y轴平移
modelMatrix.rotate(90, 0, 0, 1); // 绕Z轴旋转
// 计算模型视图投影矩阵
mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
mvpMatrix.multiply(modelMatrix); // 模型 视图投影 相乘得到最终矩阵
// 将模型视图投影矩阵传给u_MvpMatrix变量
gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);
/* 根据模型矩阵计算逆转置矩阵以变换法线 */
normalMatrix.setInverseOf(modelMatrix); // 求原矩阵的逆矩阵
normalMatrix.transpose(); // 将上一步求得的逆矩阵进行转置,并将自己设为转置后的结果
// 将用来变换法向量的矩阵传给u_NormalMatrix变量
gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}
function initVertexBuffers(gl) {
// Create a cube
// v6----- v5
// /| /|
// v1------v0|
// | | | |
// | |v7---|-|v4
// |/ |/
// v2------v3
// Coordinates
var vertices = new Float32Array([
1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0,-1.0, 1.0, 1.0,-1.0, 1.0, // v0-v1-v2-v3 front
1.0, 1.0, 1.0, 1.0,-1.0, 1.0, 1.0,-1.0,-1.0, 1.0, 1.0,-1.0, // v0-v3-v4-v5 right
1.0, 1.0, 1.0, 1.0, 1.0,-1.0, -1.0, 1.0,-1.0, -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
-1.0, 1.0, 1.0, -1.0, 1.0,-1.0, -1.0,-1.0,-1.0, -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
-1.0,-1.0,-1.0, 1.0,-1.0,-1.0, 1.0,-1.0, 1.0, -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
1.0,-1.0,-1.0, -1.0,-1.0,-1.0, -1.0, 1.0,-1.0, 1.0, 1.0,-1.0 // v4-v7-v6-v5 back
]);
// Colors
var colors = new Float32Array([
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v1-v2-v3 front
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v3-v4-v5 right
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v0-v5-v6-v1 up
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v1-v6-v7-v2 left
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // v7-v4-v3-v2 down
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0 // v4-v7-v6-v5 back
]);
// Normal
var normals = new Float32Array([
0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, // v0-v1-v2-v3 front
1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, // v0-v3-v4-v5 right
0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, // v0-v5-v6-v1 up
-1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, // v1-v6-v7-v2 left
0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, // v7-v4-v3-v2 down
0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0, 0.0, 0.0,-1.0 // v4-v7-v6-v5 back
]);
// Indices of the vertices
var indices = new Uint8Array([
0, 1, 2, 0, 2, 3, // front
4, 5, 6, 4, 6, 7, // right
8, 9,10, 8,10,11, // up
12,13,14, 12,14,15, // left
16,17,18, 16,18,19, // down
20,21,22, 20,22,23 // back
]);
// 将顶点属性写入缓冲区(坐标、颜色和法线)
if (!initArrayBuffer(gl, 'a_Position', vertices, 3)) return -1;
if (!initArrayBuffer(gl, 'a_Color', colors, 3)) return -1;
if (!initArrayBuffer(gl, 'a_Normal', normals, 3)) return -1;
gl.bindBuffer(gl.ARRAY_BUFFER, null);
var indexBuffer = gl.createBuffer();
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);
return indices.length;
}
function initArrayBuffer(gl, attribute, data, num) {
var buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
var a_attribute = gl.getAttribLocation(gl.program, attribute);
gl.vertexAttribPointer(a_attribute, num, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(a_attribute);
return true;
}
代码详解
顶点着色器的流程与LightedCube_ambient类似,区别在于,本例根据前述的规则先用模型矩阵的逆转置矩阵对a_Normal进行了变换,再赋值给normal(第14行),而不是直接赋值:

a_Normal是vec4类型的,u_NormalMatrix是mat4类型的,两者可以相乘,其结果也是vec4类型。我们只需要知道结果的前三个分量,所以就使用vec3()函数取其前3个分量,转为vec3类型。你也可以使用.xyz来这样做,比如这样写:(u_NormalMatrix*a_Normal).xyz。现在你已经了解了在物体旋转和平移时,如何变换每个顶点的法向量了。下面来看在JavaScript代码中如何计算传给着色器的u_NormalMatrix变量的矩阵。
u_NormalMatrix是模型矩阵的逆转置矩阵。示例中立方体先绕z轴旋转再沿y轴平移,所以首先使用serTranslate()和rotate()计算出模型矩阵(第63~64行);接着求模型矩阵的逆矩阵,再对结果进行转置,得到逆转置矩阵normalMatrix(第73~74行);最后,将逆转置矩阵传给着色器中的u_NormalMatrix变量(第76行)。gl.uniformMatrix4fv()函数的第2个参数指定是否对矩阵矩形转置。
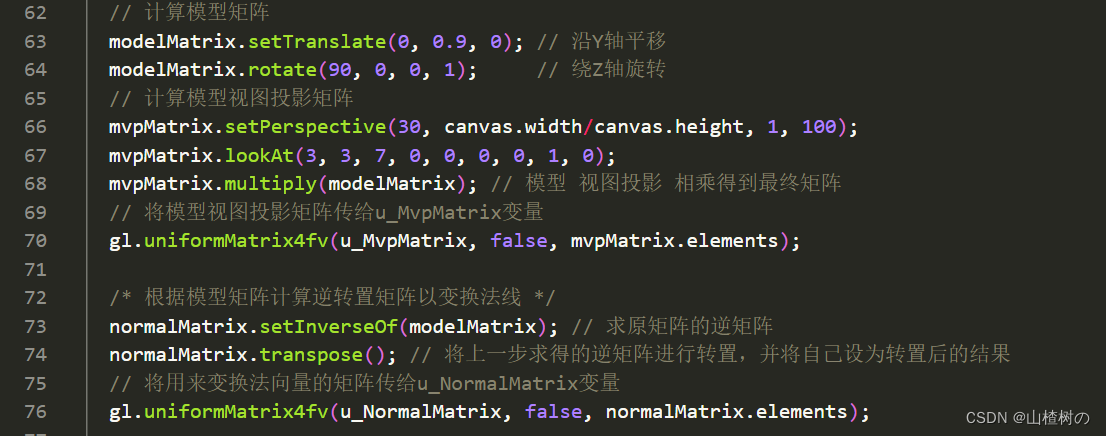
运行程序,效果如下所示。与LightedCube_ambient相比,立方体各个表面的颜色没有改变,只是位置向上移动了一段距离,这是因为:(1)平移没有改变法向量;(2)旋转虽然改变了法向量,但这里恰好旋转了90度,原来的前面现在处在右侧面的位置上,所以立方体看上去没有变化;(3)场景中的光照条件不会随着立方体位置的变化而改变;(4)漫反射光在各方向上是均匀的。
示例效果