一、行列式之前的概念
1.全排列:
把n个不同的元素排成一列,称为n个元素的全排列,简称排列
(实际上就是我们所说的排列组合,符号是A,arrange)
2.标准序列:
前一项均小于后一项的序列就是标准序列
比如 1,3,6,7,9就是标准序列
3.逆序数:
序列中满足前一项大于后一项的数对个数
比如有一个序列:{1,6,9,2,3,4}
遍历该序列,看每个数之前有几个数比它大,加和就是逆序数的值
4.奇偶排列
排列的奇偶性与逆序数的奇偶性相同
5.对换
将序列里任意两个元素交换,这个过程叫对换
对换相邻元素的,称为“相邻对换”
经过任一次对换,排列的奇偶性改变
奇排列变成标准序列的对换次数是奇数,偶排列变成标准序列的对换次数是偶数
二、N阶行列式的展开
∣ a b c d ∣ = a d − b c \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad-bc acbd =ad−bc
有n行n列的这样的式子是n阶行列式,上图为二阶行列式
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = ( a 11 ∗ a 22 ∗ a 33 ) − ( a 11 ∗ a 23 ∗ a 32 ) + ( a 12 ∗ a 23 ∗ a 31 ) − ( a 12 ∗ a 21 ∗ a 32 ) + ( a 13 ∗ a 21 ∗ a 32 ) − ( a 13 ∗ a 22 ∗ a 31 ) \begin{vmatrix} a11 & a12&a13 \\ a21 & a22&a23\\ a31&a32&a33 \end{vmatrix} = (a11*a22*a33)-(a11*a23*a32)+(a12*a23*a31)-(a12*a21*a32)+(a13*a21*a32)-(a13*a22*a31) a11a21a31a12a22a32a13a23a33 =(a11∗a22∗a33)−(a11∗a23∗a32)+(a12∗a23∗a31)−(a12∗a21∗a32)+(a13∗a21∗a32)−(a13∗a22∗a31)
而行列式的值应按照以下规则计算
按**序列奇偶性(见上文)**决定符号,并逐行把数字相乘:

我们可以把矩阵理解为一个值,甚至常数,所以它满足我们学过的一切乘法,加法性质
三、三角行列式
主对角线:左上到右下
上三角行列式的主对角线下方都是0,行列式值等于主对角线乘积
注意:左下到右上不是主对角线
1.三角行列式
上三角行列式
∣
1
2
3
0
1
2
0
0
2
∣
=
1
∗
1
∗
2
\begin{vmatrix} 1 & 2 &3\\ 0 & 1&2\\ 0&0&2 \end{vmatrix} = 1 * 1 *2
100210322
=1∗1∗2
下三角行列式
∣
1
0
0
4
1
0
3
1
2
∣
=
1
∗
1
∗
2
\begin{vmatrix} 1 & 0 &0\\ 4 & 1&0\\ 3&1&2 \end{vmatrix} = 1 * 1 *2
143011002
=1∗1∗2
对角行列式
∣
1
0
0
0
1
0
0
0
2
∣
=
1
∗
1
∗
2
\begin{vmatrix} 1 & 0 &0\\ 0 & 1&0\\ 0&0&2 \end{vmatrix} = 1 * 1 *2
100010002
=1∗1∗2
四、行列式的性质
1.转置
对每一列,从上到下书写到行上,行列式的值不变
D
=
∣
a
b
c
d
e
f
g
h
i
∣
=
D
T
=
∣
a
d
g
b
e
h
c
f
i
∣
D = \begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} =D^T= \begin{vmatrix} a & d &g\\ b & e&h\\ c&f&i \end{vmatrix}
D=
adgbehcfi
=DT=
abcdefghi
2.交换
我们可以交换行列式的任意两行或者两列,但是会导致值变为相反数
推论1:若行列式D交换一次后,仍等于D,则D=0
推论2:若行列式有两行(列)相等,则行列式为0(交换后D=-D)
∣
a
b
c
d
e
f
g
h
i
∣
=
(
−
1
)
∗
∣
a
b
c
g
h
i
d
e
f
∣
\begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} = (-1)* \begin{vmatrix} a & b &c\\ g & h&i\\ d & e&f \end{vmatrix}
adgbehcfi
=(−1)∗
agdbhecif
3.提取
我们可以把任意一个行或者一列的系数提取到行列式之前
推论:若两行(列)成比例,则行列式为0
∣ 2 a 2 b 2 c 2 d 2 e 2 f g h i ∣ = 2 ∗ ∣ 2 a 2 b 2 c d e f g h i ∣ \begin{vmatrix} 2a &2 b &2c\\ 2d & 2e&2f\\ g&h&i \end{vmatrix} =2* \begin{vmatrix} 2a & 2b &2c\\ d & e&f\\ g&h&i \end{vmatrix} 2a2dg2b2eh2c2fi =2∗ 2adg2beh2cfi
4.拆分
∣
a
+
x
b
+
y
c
+
z
d
+
w
∣
=
∣
a
b
+
y
c
d
+
w
∣
+
∣
x
b
+
y
z
d
+
w
∣
\begin{vmatrix} a +x& b+y\\ c +z& d+w\\ \end{vmatrix} = \begin{vmatrix} a & b+y\\ c & d+w\\ \end{vmatrix} + \begin{vmatrix} x& b+y\\ z& d+w\\ \end{vmatrix}
a+xc+zb+yd+w
=
acb+yd+w
+
xzb+yd+w
我们可以把行列式任意行(列)拆分成和的形式,然后转换为行列式的和
但是要注意我们每次只能拆分一行(列),多行(列)拆分是错误的
∣
a
+
x
b
+
y
c
+
z
d
+
w
∣
=
∣
a
b
c
d
∣
+
∣
x
y
z
w
∣
\cancel{ \begin{vmatrix} a +x& b+y\\ c +z& d+w\\ \end{vmatrix} = \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} x& y\\ z& w\\ \end{vmatrix}}
a+xc+zb+yd+w
=
acbd
+
xzyw
5.调整
把任意一行(列)乘以k之后可以加到另一行(列)上,行列式不变
通常这样得到三角行列式来快捷计算
∣
a
b
c
d
e
f
g
h
i
∣
=
∣
a
b
c
d
+
k
∗
a
e
+
k
∗
b
f
+
k
∗
c
g
h
i
∣
(
k
任取
)
\begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} = \begin{vmatrix} a & b &c\\ d+k *a & e+k*b&f+k*c\\ g&h&i \end{vmatrix} (k任取)
adgbehcfi
=
ad+k∗agbe+k∗bhcf+k∗ci
(k任取)
例如我们可以轻易把某些行列式调整为三角行列式
∣
1
1
2
4
3
1
3
2
2
∣
=
∣
1
1
2
0
−
1
−
7
0
−
1
−
4
∣
=
∣
1
1
2
0
−
1
−
7
0
0
3
∣
=
1
∗
(
−
1
)
∗
3
=
−
3
\begin{vmatrix} 1 & 1 &2\\ 4 & 3&1\\ 3&2&2 \end{vmatrix} = \begin{vmatrix} 1 & 1 &2\\ 0 & -1&-7\\ 0&-1&-4 \end{vmatrix} = \begin{vmatrix} 1 & 1 &2\\ 0 & -1&-7\\ 0&0&3 \end{vmatrix} = 1*(-1)*3 = -3
143132212
=
1001−1−12−7−4
=
1001−102−73
=1∗(−1)∗3=−3
五、行列式的余子式和代数余子式
1.余子式
D = ∣ a b c d e f g h i ∣ D =\begin{vmatrix} a & b &c\\ d & e&f\\ g&h&i \end{vmatrix} D= adgbehcfi
M i j 是把 D 划去第 i 行 j 列的 ( n − 1 ) 阶行列式 M_{ij}是把D划去第i行j列的(n-1)阶行列式 Mij是把D划去第i行j列的(n−1)阶行列式
M 22 = ∣ a b c d e f g h i ∣ = ∣ a c g i ∣ M_{22} = \begin{vmatrix} a & \cancel{b} &c\\ \cancel{d} & \cancel{e} & \cancel{f} \\ g& \cancel{h} &i \end{vmatrix} = \begin{vmatrix} a &c\\ g & i\\ \end{vmatrix} M22= ad gb e h cf i = agci
2.代数余子式
A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i+j} M_{ij} Aij=(−1)i+jMij
3.按行或按列展开
D
n
=
a
i
1
A
i
1
+
a
i
2
A
i
2
+
.
.
.
+
a
i
n
A
i
n
D_{n}=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}
Dn=ai1Ai1+ai2Ai2+...+ainAin
这是按行展开,其实就是对某一行遍历,然后划掉当前元素所在行列求代数余子式,然后乘当前位置的值,按列展开同理。
六、特殊行列式
1.和固定型
D n = ∣ a b b . . . b b a b . . . b b b a . . . b . . . . . . . . . . . . . . . . . . . . . . . . . . . b b b . . . b a ∣ = ∣ a + n b a + n b a + n b . . . a + n b b a b . . . b b b a . . . b . . . . . . . . . . . . . . . . . . . . . . . . . . . b b b . . . b a ∣ D_{n} =\begin{vmatrix} a & b &b&...&b\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix} = \begin{vmatrix} a+nb & a+nb &a+nb&...&a+nb\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix} Dn= abb......bbab......bbba........................bbbb...ba = a+nbbb......ba+nbab......ba+nbba........................ba+nbbb...ba
=
(
a
+
n
b
)
∣
1
1
1
.
.
.
1
b
a
b
.
.
.
b
b
b
a
.
.
.
b
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
b
b
b
.
.
.
b
a
∣
=(a+nb) \begin{vmatrix} 1 & 1 &1&...&1\\ b & a&b&...&b\\ b&b&a&...&b\\ ...&...&...&...&...\\ ...&...&...&...&b\\ b&b&...&b&a\\ \end{vmatrix}
=(a+nb)
1bb......b1ab......b1ba........................b1bb...ba
接下来就可以愉快的用第一行把行列式消成三角了
=
(
a
+
n
b
)
∣
1
1
1
.
.
.
1
0
a
−
b
0
.
.
.
0
0
0
a
−
b
.
.
.
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
0
0
.
.
.
0
a
−
b
∣
=
(
a
−
b
)
n
−
1
=(a+nb) \begin{vmatrix} 1 & 1 &1&...&1\\ 0 & a-b&0&...&0\\ 0&0&a-b&...&0\\ ...&...&...&...&...\\ ...&...&...&...&0\\ 0&0&...&0&a-b\\ \end{vmatrix} = (a-b)^{n-1}
=(a+nb)
100......01a−b0......010a−b........................0100...0a−b
=(a−b)n−1
2.范德蒙德行列式
D n = ∣ x 1 0 x 2 0 x 3 0 . . . x n 0 x 1 1 x 2 1 x 3 1 . . . x n 1 x 1 2 x 2 2 x 3 2 . . . x n 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . x n n − 1 x 1 n x 2 n x 3 n . . . x n n ∣ = ∣ 1 1 1 . . . 1 x 1 1 x 2 1 x 3 1 . . . x n 1 x 1 2 x 2 2 x 3 2 . . . x n 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . x n n − 1 x 1 n x 2 n x 3 n . . . x n n ∣ D_{n} = \begin{vmatrix} x_1^0 & x_2^0 &x_3^0&...&x_n^0\\ x_1^1 & x_2^1 &x_3^1&...&x_n^1\\ x_1^2 & x_2^2 &x_3^2&...&x_n^2\\ ...&...&...&...&...\\ ...&...&...&...&x_n^{n-1}\\ x_1^n & x_2^n&x_3^n&...&x_n^n\\ \end{vmatrix}=\begin{vmatrix} 1 & 1 &1&...&1\\ x_1^1 & x_2^1 &x_3^1&...&x_n^1\\ x_1^2 & x_2^2 &x_3^2&...&x_n^2\\ ...&...&...&...&...\\ ...&...&...&...&x_n^{n-1}\\ x_1^n & x_2^n&x_3^n&...&x_n^n\\ \end{vmatrix} Dn= x10x11x12......x1nx20x21x22......x2nx30x31x32......x3n..................xn0xn1xn2...xnn−1xnn = 1x11x12......x1n1x21x22......x2n1x31x32......x3n..................1xn1xn2...xnn−1xnn
这样的行列式称为“范德蒙德行列式”
一般按照以下规则计算
D n = ∏ 1 < = i < j < = n ( x j − x i ) = − − − − − − − − − − − − − − − − − − − − − − − − − − − − ( x n − x n − 1 ) ( x n − x n − 2 ) . . . ( x n − x 1 ) ( x n − 1 − x n − 2 ) ( x n − 1 − x n − 3 ) . . . ( x n − 1 − x 1 ) . . . ( x 3 − x 2 ) ( x 3 − x 1 ) ( x 2 − x 1 ) D_n = \prod_{1<=i<j<=n}{(x_j-x_i)} = \\ ----------------------------\\ (x_n-x_{n-1})(x_n-x_{n-2})...(x_n-x_{1})\\(x_{n-1}-x_{n-2})(x_{n-1}-x_{n-3})...(x_{n-1}-x_{1})\\ ...\\ (x_{3}-x_{2})(x_{3}-x_{1})\\ (x_{2}-x_{1}) Dn=∏1<=i<j<=n(xj−xi)=−−−−−−−−−−−−−−−−−−−−−−−−−−−−(xn−xn−1)(xn−xn−2)...(xn−x1)(xn−1−xn−2)(xn−1−xn−3)...(xn−1−x1)...(x3−x2)(x3−x1)(x2−x1)
证明过程如下


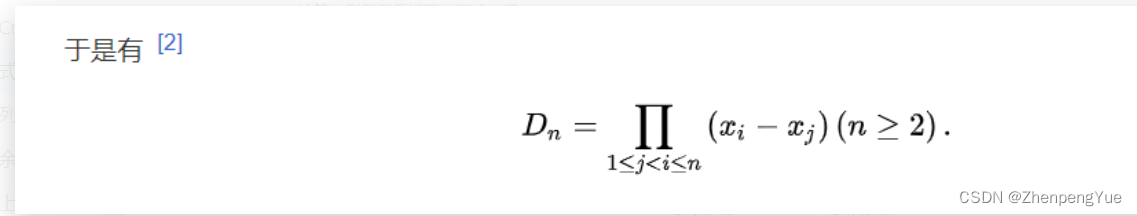
七、克莱姆法则(Cramer’s Rule)
{
a
11
x
1
+
a
12
x
2
+
a
13
x
3
+
.
.
.
+
a
1
n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+
a
23
x
3
+
.
.
.
+
a
2
n
x
n
=
b
2
.
.
.
a
n
1
x
1
+
a
n
2
x
2
+
a
n
3
x
3
+
.
.
.
+
a
n
n
x
n
=
b
n
\begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases}
⎩
⎨
⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
对于这样一个方程组,我们定义一个行列式,只存它的系数,称为”系数行列式”
D
n
=
∣
a
11
a
12
a
13
.
.
.
a
1
n
a
21
a
22
a
23
.
.
.
a
2
n
a
31
a
32
a
33
.
.
.
a
3
n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
(
n
−
1
)
n
a
n
1
a
n
2
.
.
.
a
n
(
n
−
1
)
a
n
n
∣
D_{n} =\begin{vmatrix} a_{11} & a_{12} &a_{13}&...&a_{1n}\\ a_{21} & a_{22}&a_{23}&...&a_{2n}\\ a_{31}&a_{32}&a_{33}&...&a_{3n}\\ ...&...&...&...&...\\ ...&...&...&...&a_{(n-1)n}\\ a_{n1}&a_{n2}&...&a_{n(n-1)}&a_{nn}\\ \end{vmatrix}
Dn=
a11a21a31......an1a12a22a32......an2a13a23a33........................an(n−1)a1na2na3n...a(n−1)nann
应用:克莱姆法则判断具有N个方程、N个未知数的线性方程组的解:
- 当方程组的系数行列式不等于零时,方程组且具有唯一解;
- 如果方程组无解或者有两个不同的解,方程组的系数行列式等于零
- 克莱姆法则不仅仅适用于实数域,它在任何域上面都成立。
克莱姆法则的局限性:
- 方程个数与未知数的个数不同时,系数的行列式等于零时,克莱姆法则失效。
- 运算量较大,求解一个N阶线性方程组要计算N+1个N阶行列式