皮克定理

皮克定理：皮克定理是指一个计算所有顶点坐标为整数的多边形面积公。该公式可以表示为S=a+b÷2－1，其中a表示多边形内部的坐标为整数的点数，b表示多边形边上且坐标为整数的点数，S表示多边形的面积。

举个简单的例子。
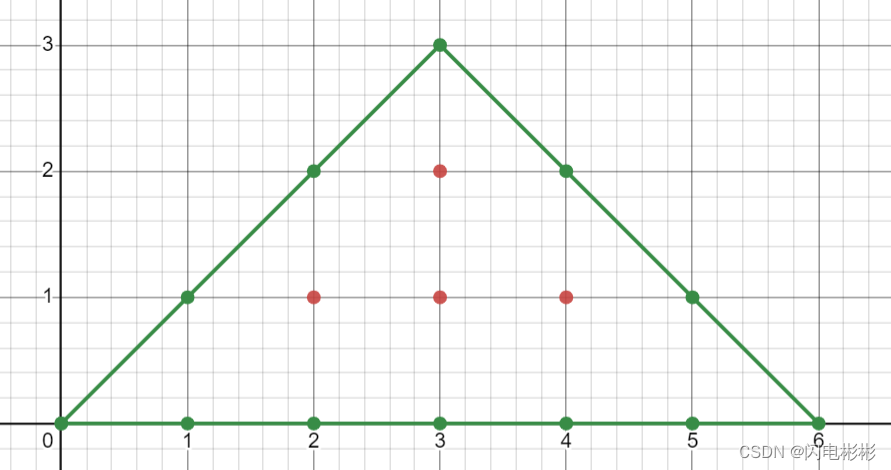
在这里插入图片描述
上图中，边上的整格点数量b=12, 内部点数量a = 4
那么三角形面积S = 4+12/2-1 = 9

多边形面积算法

对于多边，可以任选一个点O，然后把多边形顶点按照逆时针排序，遍历所有点和后一个点与O连成一个三角形，计算出所有三角形面积，并求和即可。
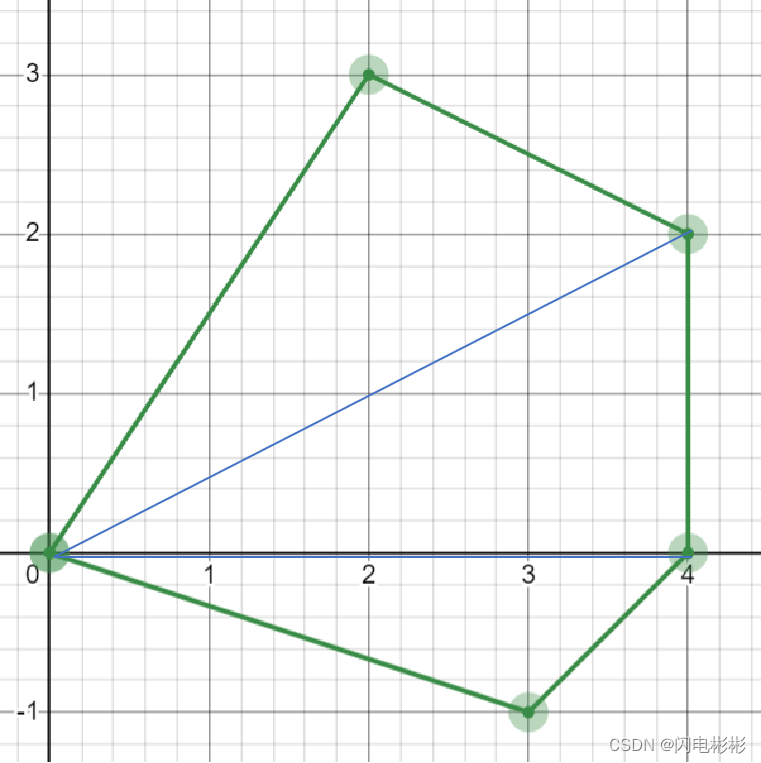
在这里插入图片描述
如上图所示，绿线为多边形，通过分割成多个三角形来计算面积。
计算面积时利用向量叉乘即可。
这个算法对于非凸多边形也适用。

面积公式应用

http://poj.org/problem?id=1654

题目大意

一个多边形起点从0点出发，每次沿8个方向中的1个方向，行走不超过1个格子。求最后合围区域面积。

代码

需要用c++提交
需要用c++提交
需要用c++提交

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>


using namespace std;

int gcd(int a, int b) {
	if (a < 0 || b < 0)return gcd(abs(a), abs(b));
	if (a > b)return gcd(b, a);
	if (a == 0)return b;
	return gcd(b % a, a);
}
typedef long long lld;
int dir[10][2] = {
	{-1,-1},
	{0,-1},
	{1,-1},
	{-1,0},
	{0,0},
	{1,0},
	{-1,1},
	{0,1},
	{1,1},
};
// 2A = 2s+p-2
char str[1000000 + 10];
void solve() {
	int T;
	scanf("%d", &T);
	while (T--) {
		scanf("%s", str);
		pair<lld, lld> pre(0, 0), now;
		lld area = 0;
		for (int i = 0; str[i] != '5'; ++i) {
			int d = str[i] - '1';
			now.first = pre.first + dir[d][0];
			now.second = pre.second+ dir[d][1];
			area += pre.first * now.second - pre.second * now.first;
			pre = now;
		}

		if(area<0)area = -(area);
		printf("%lld",area/2);
		if (area & 1) {
			printf(".5");
		}
		puts("");
	}
}

int main() {
	solve();
	return 0;
}

皮克定理应用一

http://poj.org/problem?id=2954

题目大意

给定1个三角形，顶点都是整数，求内部整数点数量。

思路

通过顶点求出面积。
三条边的坐标，可以求出3条边经过整点的数量。
利用公式即可求出内部点。

代码

需要用c++提交
需要用c++提交
需要用c++提交

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>


using namespace std;

int gcd(int a, int b) {
	if (a < 0 || b < 0)return gcd(abs(a), abs(b));
	if (a > b)return gcd(b, a);
	if (a == 0)return b;
	return gcd(b % a, a);
}
// 2A = 2s+p-2
void solve() {
	int x1, y1, x2, y2, x3, y3;
	while(scanf("%d%d%d%d%d%d", &x1, &y1, &x2, &y2, &x3, &y3) != EOF) {
		if (x1 == 0 && x2 == 0 && x3 == 0 && y1 == 0 && y2 == 0 && y3 == 0)break;
		int edgePoints = 0;
		pair<int, int>p0(x2 - x1, y2 - y1);
		pair<int, int>p1(x3 - x2, y3 - y2);
		pair<int, int>p2(x1 - x3, y1 - y3);
		int area = abs(p0.first*p1.second - p0.second*p1.first);
		edgePoints += gcd(p0.first, p0.second);
		edgePoints += gcd(p1.first, p1.second);
		edgePoints += gcd(p2.first, p2.second);

		int innerPoint = (area - edgePoints) / 2 +1;
		printf("%d\n", innerPoint);
		
	}
}

int main() {
	solve();
	return 0;
}

皮克定理应用二

http://poj.org/problem?id=1265

题目大意

给定机器人每次行走的向量，求最后合围区域的内部点，边界点，和面积。

思路

通过顶点求出面积。
每条边上的顶点可以单独求出。
利用公式即可求出内部点。

代码

需要用c++提交
需要用c++提交
需要用c++提交

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>


using namespace std;

int gcd(int a, int b) {
	if (a < 0 || b<0)return gcd(abs(a), abs(b));
	if (a > b)return gcd(b, a);
	if (a == 0)return b;
	return gcd(b % a, a);
}
// 2A = 2s+p-2
void solve() {
	int T;
	scanf("%d", &T);
	int N;
	for (int k = 1; k <= T;++k) {
		scanf("%d", &N);
		int edgePoints = 0;
		pair<int, int> p0(0,0);
		pair<int, int> pre=p0, now;
		int area = 0;
		for (int i = 0; i < N; ++i) {
			scanf("%d %d", &now.first, &now.second);

			edgePoints += gcd(now.first, now.second);
			now.first += pre.first;
			now.second += pre.second;
			area += pre.first * now.second - pre.second * now.first;
			pre = now;
		}

		area = abs(area);
		int innerPoint = (area + 2 - edgePoints) / 2;
		printf("Scenario #%d:\n", k);
		printf("%d %d %.1f\n\n", innerPoint, edgePoints, area*1.0/2);
	}
}

int main() {
	solve();
	return 0;
}

/*
2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

*/