什么是跨域
要了解跨域,首先得知道浏览器的同源策略。
同源策略:是由Netscape提出的一个安全策略,能够阻挡恶意文档,保护本地数据。它能限制一个源的文档或脚本对另一个源的交互,使得其它源的文档或脚本,无法读取或修改当前源。
是否同源:当两个url的域名、协议和端口均相同。
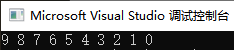
举例来说:url: http://127.0.0.1:80/demo/01.html 中组成部分如下图所示:

| url | 是否同源 | 原因 |
| http://127.0.0.1:80/demo/02.html http://127.0.0.1:80/demo2/01.html | 同源 | 协议、域名、端口均相同,只是文件地址不同 |
| http://127.0.0.1:90/demo/01.html | 不同源 | 端口不同 |
| http://127.1.1.1:80/demo/01.html | 不同源 | 域名不同 |
| https://127.0.0.1:80/demo/01.html | 不同源 | 协议不同 |
| http://127.0.0.1/demo/01.html | 同源 | http:// 默认端口是 80 |
不同协议有不同的默认端口,当未指定端口时,则使用默认端口。
跨域:能实现在不同源之间的资源交互。
为什么要跨域:因为所有的资源有可能不在同一个域内,比如一个公司有很多子域,中间的通信就需要跨域。
vue项目跨域vue.config.js文件配置
1. publicPath配置
publicPath是部署时的基本url,一般情况下vue项目起什么名称,publicPath就赋值什么名称。
假设一个项目的初始地址为: http://127.0.0.1:80/,若是配置上publicPath: "/demo",则项目的初始地址则会变成http://127.0.0.1:80/demo/。
vue打包后的静态文件资源需要访问,所以需要一个文件路径放置vue的打包文件,后端nginx中对应配置的也是这个地址。
2. devServer.proxy代理配置
该字段主要是为了实现前后端通信的,当前后端分离开发,为了让前端开发人员在开发时访问到后端的接口,需要进行nginx配置实现跨域请求。
参考这个同学的文章:vue配置反向代理 devServer配置proxy,说明如下:
// vue.config.js文件
module.exports = {
//.....devServer: {host: 'localhost',port: 8080,proxy: {"/api": {target: "http://www.xxx.com", // 请求到/api/xx 就会被代理http://www.xxx.com/api/xxx// secure: false, // 如果是https接口,需要配置这个参数changeOrigin: true, // 接口跨域 需打开这个参数pathRewrite: {'^/api': '', // 忽略前缀/api 则会被代理到http://www.xxx.com/xxx},}}},
}
其实很好理解,简单来说就是给实际的接口路径做了一层代理。
”/api”含义:匹配以”/api”开头接口,
target参数含义:默认将上面的"/api"拼接到该值的后面,映射成代理的实际路径。
举例:请求接口时如果写的是“/api/xxx”,使用代理后生成的实际请求路径就是’http://www.xxx.com/api/xxx’。
pathRewrite参数含义:路径重写,如果要请求的接口里面没有公共的api,直接从根目录开始的,那就需要把"/api"去掉或换成其它别的字符。