欢~迎~光~临~^_^
目录
知识树
1、什么是串的模式匹配
2、简单的模式匹配算法
3、KMP算法
3.1 算法原理
3.2 C语言实现KMP算法
3.3 求next数组
3.4 KMP算法优化(对next数组的优化)
知识树
 1、什么是串的模式匹配
1、什么是串的模式匹配
串的模式匹配是在一个字符串中查找另一个较小的字符串(称为模式)的过程。模式匹配的目的是在文本串中查找一个或多个匹配字符串。这种搜索可以使用各种算法进行,包括暴力算法,KMP算法和Boyer-Moore算法等。模式匹配广泛应用于文本编辑器、搜索引擎、计算机网络和计算机安全等领域。
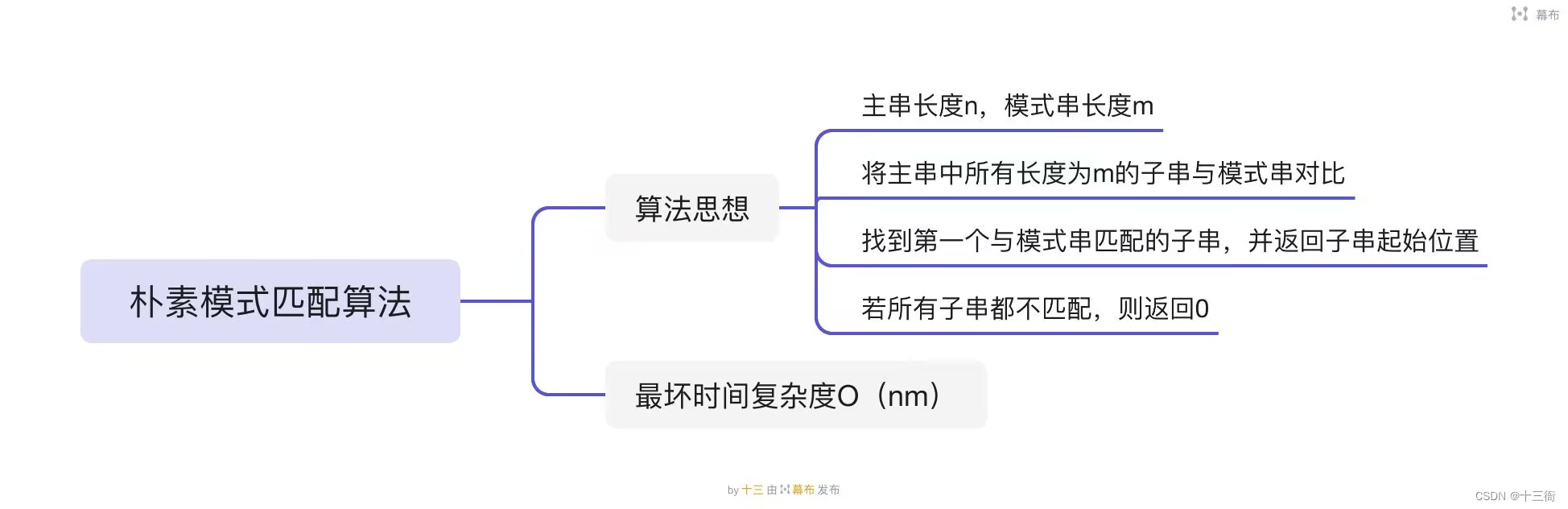
2、简单的模式匹配算法
这个算法的时间复杂度是O(mn),其中m是模式串的长度,n是文本串的长度。在最坏情况下,即文本串中的每个字符都匹配模式串中的每个字符,时间复杂度为O(m(n-m+1)),因此朴素模式匹配算法在处理大型文本串时可能会变得很慢。
#include <stdio.h>
#include <string.h>
int naive_search(const char text[], const char pattern[]) {
int text_len = strlen(text);
int pattern_len = strlen(pattern);
for (int i = 0; i <= text_len - pattern_len; i++) {
int j;
for (j = 0; j < pattern_len; j++) {
if (text[i + j] != pattern[j])
break;
}
if (j == pattern_len)
return i;
}
return -1;
}
int main() {
char text[] = "ABABCABCABABABD";
char pattern[] = "ABABD";
int pos = naive_search(text, pattern);
if (pos >= 0)
printf("Pattern found at position %d in the text.", pos);
else
printf("Pattern not found in the text.");
return 0;
}
3、KMP算法
3.1 算法原理
KMP算法是一种字符串匹配算法,它的原理是利用已知的信息尽可能减少匹配次数。KMP算法的核心是一个跳转表格,也称为Next数组或失配函数。
在匹配的过程中,当发现不匹配的情况时,KMP算法会利用跳转表格中已经计算好的信息,直接跳过部分不需要匹配的字符,从而减少匹配次数。具体来说,KMP算法会根据当前匹配的位置和已知的信息,计算出下一个字符需要匹配的位置,从而避免了不必要的匹配操作。
KMP算法的时间复杂度为O(m+n),其中m和n分别为模式串和文本串的长度,求next数组时间复杂度O(m);模式匹配过程最坏时间复杂度O(n)。相比于朴素的字符串匹配算法,KMP算法在匹配效率和性能上有了很大的提高。
3.2 C语言实现KMP算法
下述代码中,next()函数用于计算模式串的next数组,kmp()函数用于在文本串中查找模式串。在main()函数中,首先输入文本串和模式串,然后调用next()函数生成模式串的next数组,最后调用kmp()函数在文本串中查找模式串。若模式串存在于文本串中,输出模式串在文本串中的位置,否则输出不存在的信息。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void next(char *pattern, int *next_arr) {
int i = 0, j = -1;
next_arr[0] = -1;
int len = strlen(pattern);
while (i < len - 1) {
if (j == -1 || pattern[i] == pattern[j]) {
i++;
j++;
next_arr[i] = j;
} else {
j = next_arr[j];
}
}
}
int kmp(char *text, char *pattern, int *next_arr) {
int i = 0, j = 0;
int text_len = strlen(text), pattern_len = strlen(pattern);
while (i < text_len && j < pattern_len) {
if (j == -1 || text[i] == pattern[j]) {
i++;
j++;
} else {
j = next_arr[j];
}
}
if (j == pattern_len) {
return i - j;
} else {
return -1;
}
}
int main() {
char text[100], pattern[100];
int next_arr[100];
printf("请输入文本串:");
gets(text);
printf("请输入模式串:");
gets(pattern);
next(pattern, next_arr);
int index = kmp(text, pattern, next_arr);
if (index != -1) {
printf("模式串在文本串中的位置是:%d\n", index);
} else {
printf("文本串中不存在模式串!\n");
}
return 0;
}
3.3 求next数组
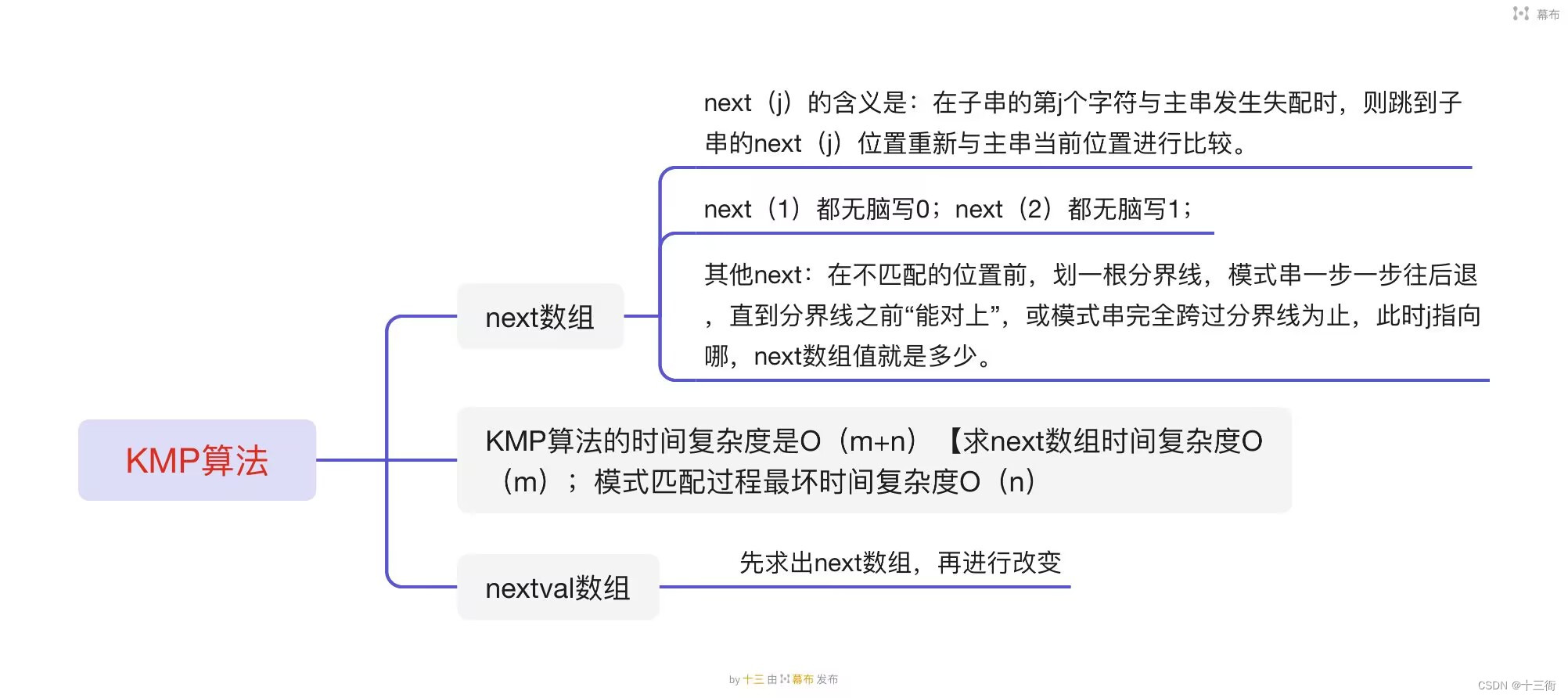
next(j)的含义是:在子串的第j个字符与主串发生失配时,则跳到子串的next(j)位置重新与主串当前位置进行比较。
next(1)都无脑写0;next(2)都无脑写1;
其他next:在不匹配的位置前,划一根分界线,模式串一步一步往后退,直到分界线之前“能对上”,或模式串完全跨过分界线为止,此时 j 指向哪,next数组值就是多少。
void next(char *pattern, int *next_arr) {
int i = 0, j = -1;
next_arr[0] = -1;
int len = strlen(pattern);
while (i < len - 1) {
if (j == -1 || pattern[i] == pattern[j]) {
i++;
j++;
next_arr[i] = j;
} else {
j = next_arr[j];
}
}
}
在上述代码中,pattern表示模式串,next_arr表示next数组。首先将next_arr[0]置为-1,i表示当前已匹配的字符数,初始值为0,j表示当前已匹配的字符中,能和下一位字符匹配的最长前缀的末尾位置,初始值为-1。在循环中,若第i个字符能和第j+1个字符匹配,则更新next_arr[i+1]=j+1,否则将j更新为next_arr[j],重复此过程直到结束。
例1,若模式串为
ABCDABD,则next数组为[-1, 0, 0, 0, 0, 1, 2, 0]。
例2,下面是"ababaaababaa"模式串对应的next数组值:
- a b a b a a a b a b a a
- 0 0 1 2 3 4 5 2 3 4 5 6因此,"ababaaababaa"模式串的next数组值为[0, 0, 1, 2, 3, 4, 5, 2, 3, 4, 5, 6]。
next数组的生成过程是KMP算法的核心部分,它可以大大提高模式匹配的效率。
3.4 KMP算法优化(对next数组的优化)
KMP算法优化:可以采用KMP算法的优化手段,通过推导next[j]和nextval[next[j]]的关系,减少计算次数。
//核心代码
nextval[1]=0;
for(int j = 2;j < pattern.length;j++)
{
if(pattern[next[j]] == pattern[j])
nextval[j] = nextval[next[j]];
else
nextval[i] = nextval[j];
}🤞❤️🤞❤️🤞❤️串的模式匹配的知识点总结就到这里啦,如果对博文还满意的话,劳烦各位看官动动“发财的小手”留下您对博文的赞和对博主的关注吧🤞❤️🤞❤️🤞❤️