滑动时间窗口的思想和实现，环形数组，golang

news2024/11/17 9:40:02

固定时间窗口

在开发限流组件的时候，我们需要统计一个时间区间内的请求数，比如以分钟为单位。所谓固定时间窗口，就是根据时间函数得到当前请求落在哪个分钟之内，我们在统计的时候只关注当前分钟之内的数量，即 [0s, 60s]，因为流量并不是均匀的，所以就会出现，在两个分钟之间超过阈值，1分50秒时来了150个请求，在2分10秒时来了150个请求，如果我们设置的阈值是200，这就超过了阈值，这会对系统造成隐患。

固定时间窗口的主要特征是：取样窗口直接从当前分钟跳到下一分钟。

滑动时间窗口

如果一个请求到达，我们根据请求的时间，倒推一分钟，然后统计此区间的请求数，来判断是否超过阈值，这就是滑动窗口，即，窗口是缓慢滑动的。显然这种方式效率不高，每次都要统计。

做一个折中，将一分钟分成10个小窗口，每个请求都落到其中一个小窗口上，每次以小窗口为单位移动，并且请求数实时统计到小窗口中，这样只需要将10个窗口加起来和阈值比较。

实现原理

此处可以参考环形队列的设计思想，采样长度为10的数组作为小窗口，一个游标指向最新的窗口（时间最新），如果窗口发生了滑动，就将游标移动到特定位置。

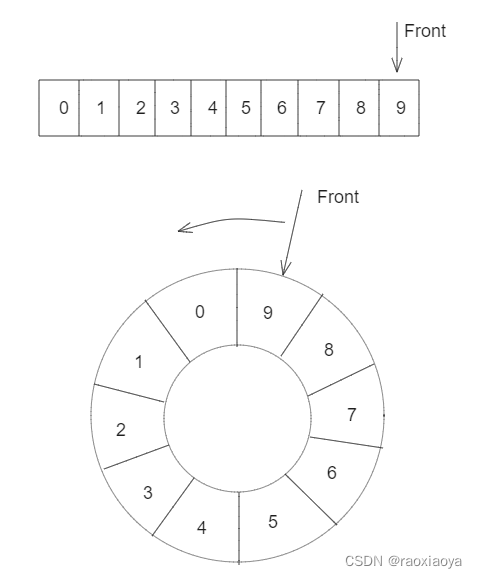
在这里插入图片描述

由于请求的到来不是连续的，所以Front的移动可能是跳跃式的。

每向前滑动一个小窗口，就意味着头部增加一个，尾部舍弃一个，如果发生了跳跃，那么尾部要舍弃多个，同时中间要补0。即，从第二圈开始，Front 划过的地方都要被置为0。

简单模拟如下，第一行值为9的地方为Front，向右滑动，来到第二行，依次类推。在第四行时出现了跳跃。

0	1	2	3	4	5	6	7	8	9
	1	2	3	4	5	6	7	8	9	x
		2	3	4	5	6	7	8	9	x	y
					5	6	7	8	9	x	y	0	0	z

整理
0	1	2	3	4	5	6	7	8	9
x	1	2	3	4	5	6	7	8	9
x	y	2	3	4	5	6	7	8	9
x	y	0	0	z	5	6	7	8	9

算法与测试

package plugin

import (
	"log"
	"time"
)

// 滑动窗口
type WindowLeapArray struct {
	Arr                 []int // 窗口数据
	WindowsNum          int   // 样本窗口个数，设置为10
	Front               int   // 游标
	FrontTime           int64 // 游标最新时间
	RequestNumPerSecond int   // 限制请求数
	WindowStatus        bool  // 窗口状态，true 为 拒绝访问
}

func NewWindowLeapArray(requestNumPerSecond int) *WindowLeapArray {
	return &WindowLeapArray{
		Arr:                 make([]int, 10),
		WindowsNum:          10,
		RequestNumPerSecond: requestNumPerSecond,
	}
}

// GlobalCheck 全局限流
func (w *WindowLeapArray) GlobalCheck() bool {
	timenow := time.Now()

	start := w.FrontTime

	frontTimeLeft := timenow.UnixMilli() - timenow.UnixMilli()%100
	index := (timenow.UnixMilli() - 1000*timenow.Unix()) / 100

	if w.FrontTime == 0 {
		// 记为小窗口的左侧时间 1694678187869 -> 1694678187800
		w.FrontTime = frontTimeLeft
		w.Front = int(index)
		w.Arr[w.Front]++

		log.Println(timenow.UnixMilli(), start, (timenow.UnixMilli()-start)/100, w.Arr)
		return true
	}

	// 时间差
	gaptime := (timenow.UnixMilli() - w.FrontTime)

	if gaptime < 100 {
		// 同一小窗口

		if w.WindowStatus {
			log.Println(timenow.UnixMilli(), start, (timenow.UnixMilli()-start)/100, w.Arr)
			return false
		}

		// 统计
		var sum int
		for _, v := range w.Arr {
			sum = sum + v
		}
		if sum >= w.RequestNumPerSecond {
			w.WindowStatus = true
			log.Println(timenow.UnixMilli(), start, (timenow.UnixMilli()-start)/100, w.Arr)
			return false
		} else {
			w.Arr[w.Front]++
		}
	} else {
		// 滑动，采用环形数组
		// 可能存在跳跃

		w.WindowStatus = false
		w.FrontTime = frontTimeLeft

		gap := gaptime / 100
		if gap >= 10 {
			for i := 0; i < 10; i++ {
				w.Arr[i] = 0
			}
		} else {
			for i := 1; i <= int(gap); i++ {
				tmp := w.Front + i
				if tmp >= 10 {
					tmp = tmp - 10
				}
				w.Arr[tmp] = 0
			}
		}

		w.Front = int(index)

		// 统计
		var sum int
		for _, v := range w.Arr {
			sum = sum + v
		}
		if sum >= w.RequestNumPerSecond {
			w.WindowStatus = true
			log.Println(timenow.UnixMilli(), start, (timenow.UnixMilli()-start)/100, w.Arr)
			return false
		} else {
			w.Arr[w.Front] = 1
		}
	}
	log.Println(timenow.UnixMilli(), start, (timenow.UnixMilli()-start)/100, w.Arr)

	return true
}

单元测试

func TestFun(t *testing.T) {
	w := plugin.NewWindowLeapArray(10)
	for i := 0; i < 30; i++ {
		re := w.GlobalCheck()
		log.Println(re)
		n := util.RandInt(30, 3000)
		time.Sleep(time.Duration(n) * time.Millisecond)
	}
}

输出

2023/09/15 11:48:09 1694749689568 0 16947496895 [0 0 0 0 0 1 0 0 0 0]
2023/09/15 11:48:09 true
2023/09/15 11:48:11 1694749691250 1694749689500 17 [0 0 1 0 0 0 0 0 0 0]
2023/09/15 11:48:11 true
2023/09/15 11:48:12 1694749692007 1694749691200 8 [1 0 1 0 0 0 0 0 0 0]
2023/09/15 11:48:12 true
2023/09/15 11:48:12 1694749692083 1694749692000 0 [2 0 1 0 0 0 0 0 0 0]
2023/09/15 11:48:12 true
2023/09/15 11:48:13 1694749693857 1694749692000 18 [0 0 0 0 0 0 0 0 1 0]
2023/09/15 11:48:13 true
2023/09/15 11:48:14 1694749694213 1694749693800 4 [0 0 1 0 0 0 0 0 1 0]
2023/09/15 11:48:14 true
2023/09/15 11:48:15 1694749695227 1694749694200 10 [0 0 1 0 0 0 0 0 0 0]
2023/09/15 11:48:15 true
2023/09/15 11:48:15 1694749695388 1694749695200 1 [0 0 1 1 0 0 0 0 0 0]
2023/09/15 11:48:15 true
2023/09/15 11:48:16 1694749696076 1694749695300 7 [1 0 1 1 0 0 0 0 0 0]
2023/09/15 11:48:16 true
2023/09/15 11:48:16 1694749696590 1694749696000 5 [1 0 0 0 0 1 0 0 0 0]
2023/09/15 11:48:16 true
2023/09/15 11:48:18 1694749698828 1694749696500 23 [0 0 0 0 0 0 0 0 1 0]
2023/09/15 11:48:18 true
2023/09/15 11:48:20 1694749700913 1694749698800 21 [0 0 0 0 0 0 0 0 0 1]
2023/09/15 11:48:20 true
2023/09/15 11:48:22 1694749702052 1694749700900 11 [1 0 0 0 0 0 0 0 0 0]
2023/09/15 11:48:22 true
2023/09/15 11:48:23 1694749703076 1694749702000 10 [1 0 0 0 0 0 0 0 0 0]
2023/09/15 11:48:23 true
2023/09/15 11:48:23 1694749703422 1694749703000 4 [1 0 0 0 1 0 0 0 0 0]
2023/09/15 11:48:23 true
2023/09/15 11:48:23 1694749703781 1694749703400 3 [1 0 0 0 1 0 0 1 0 0]
2023/09/15 11:48:23 true
2023/09/15 11:48:23 1694749703990 1694749703700 2 [1 0 0 0 1 0 0 1 0 1]
2023/09/15 11:48:23 true
2023/09/15 11:48:26 1694749706029 1694749703900 21 [1 0 0 0 0 0 0 0 0 0]
2023/09/15 11:48:26 true
2023/09/15 11:48:28 1694749708168 1694749706000 21 [0 1 0 0 0 0 0 0 0 0]
2023/09/15 11:48:28 true
2023/09/15 11:48:29 1694749709514 1694749708100 14 [0 0 0 0 0 1 0 0 0 0]
2023/09/15 11:48:29 true
2023/09/15 11:48:30 1694749710850 1694749709500 13 [0 0 0 0 0 0 0 0 1 0]
2023/09/15 11:48:30 true
......