深度优先搜索算法与广度优先搜索算法及其C++、MATLAB代码迷宫应用
- 1. 深度优先搜索算法(DFS)
- 1.1 深度优先搜索伪代码:
- 1.2 案例应用:迷宫最小步数
- 1.2.1 DFS算法MATLAB代码
- 1.2.1 DFS算法C++代码
- 2. 广度优先搜索算法(BFS)
- 2.1 广度优先搜索伪代码:
- 2.2 案例应用:迷宫最小步数
- 2.2.1 BFS算法C++代码
- 3. DFS与BFS的比较
- 4. 共同缺点
- 5. 结论
引言: 在计算机科学领域,搜索算法是一种基本的技术,用于解决各种问题,从图论中的路径查找到数据结构中的遍历。深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的搜索算法,它们在不同的情境下表现出色。本文将介绍这两种经典的搜索算法,以及它们的应用和差异,并附加中文伪代码来更好地理解算法。
1. 深度优先搜索算法(DFS)
深度优先搜索算法:一种用于遍历或搜索树或图的算法。通过探索一个路径的尽头,然后回溯到之前的节点,再继续探索其他路径的算法。这一过程可以看作是一种递归的方式,深入地搜索树的分支,直到找到目标或遍历完整棵树。
如图所示,注意观察搜索树的序号,总是优先探索可扩展节点的第一个节点,遇到障碍回溯到最近未探索节点:
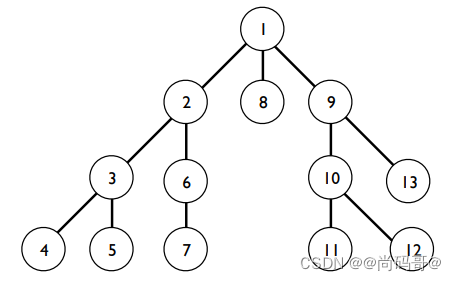
注意: 在非常深的搜索空间中,算法可能会陷入越来越深的搜索空间中(递归算法可能会递归得太深,以至于计算机耗尽内存)。为了避免这种陷阱,我们需要设置一个深度限制,使得算法可以在不超出一定深度的情况下进行回溯。该算法的这种变体称为深度有限搜索(Depth-limited search)。
1.1 深度优先搜索伪代码:
# 伪代码实现DFS
function dfs(node):
if node is goal:
return True # 找到目标
visited[node] = True
for each neighbor of node:
if not visited[neighbor]:
if dfs(neighbor):
return True
return False
1.2 案例应用:迷宫最小步数
起点:1 1
终点:4 3
地图:0代表障碍物,1代表通道
1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0
求到达目标点的最小步数
1.2.1 DFS算法MATLAB代码
global min_step end_xy map mark direction
map=[1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0];
mark = zeros(size(map));
direction = [ 1 0
0 -1
-1 0
0 1];
start_xy = [1 1];
end_xy = [4 3];
min_step = 9999; step = 0;
dfs(start_xy,step);
disp(min_step);
function dfs(point_xy,step)
global min_step end_xy map mark direction;
if point_xy(1) == end_xy(1) && point_xy(2) == end_xy(2)
if min_step > step
min_step = step;
end
return;
end
for i=1:4
temp = point_xy+direction(i,:);
if temp(1) < 1 || temp(1) > size(map,1) || temp(2) < 1|| temp(2) > size(map,2)
continue;
end
if map(temp(1),temp(2))==1 && mark(temp(1),temp(2)) == 0
mark(temp(1),temp(2)) = 1;
dfs(temp,step+1);
mark(temp(1),temp(2)) = 0;
end
end
return;
end
1.2.1 DFS算法C++代码
#include<cstdio>
using namespace std;
int start_x,start_y,end_x,end_y,width,height,min_step =9999;
int map[100][100]={0}; //1 表示通道 0 表示障碍物
int mark[100][100]={0}; //1 表示访问 0 表示未访问
int direction[4][2]={{1,0},{0,-1},{-1,0},{0,1}};
void dfs(int x, int y, unsigned int step)
{
if(x == end_x && y == end_y)
{
if(step < min_step)
{
min_step = step;
}
return;
}
for(int i=0; i<4; i++)
{
int temp_x = x+direction[i][0];
int temp_y = y+direction[i][1];
if (temp_x <1 || temp_y < 1 || temp_x > height || temp_y>width)
continue;
if(map[temp_x][temp_y]==1 && mark[temp_x][temp_y]==0)
{
mark[temp_x][temp_y] = 1;
dfs(temp_x,temp_y,step+1);
mark[temp_x][temp_y] = 0;
}
}
return;
}
/*
5 4
1 1 4 3
1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0
*/
int main()
{
scanf("%d%d", &height,&width);
scanf("%d%d%d%d", &start_x, &start_y, &end_x, &end_y);
for(int i=1; i<=height; i++)
for(int j=1; j<=width; j++)
scanf("%d",&map[i][j]);
mark[start_x][start_y] = 1;
dfs(start_x, start_y, 0);
printf("%d",min_step);
return 0;
}
2. 广度优先搜索算法(BFS)
广度优先搜索算法是一种逐层扩展搜索的算法,它从起始节点开始,首先探索所有与该节点直接相连的节点,然后再探索这些节点的邻居节点,以此类推,直到找到目标或遍历整个图。
如图所示,注意观察搜索树的序号,总是优先探索可扩展节点的所有节点,直到找到目标或遍历整个图:
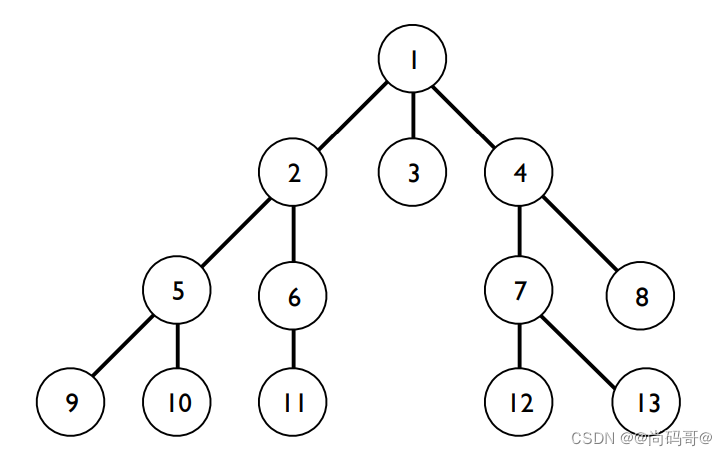
注意: 在一个非常广阔的搜索空间中,这个算法可能会陷入存储一层的所有节点的困境,然后才能进入下一层。每层的节点数量呈指数增长。
2.1 广度优先搜索伪代码:
# 伪代码实现BFS
function bfs(start, goal):
queue = Queue()
queue.enqueue(start)
visited = set()
while not queue.isEmpty():
node = queue.dequeue()
if node == goal:
return True # 找到目标
visited.add(node)
for each neighbor of node:
if neighbor not in visited and neighbor not in queue:
queue.enqueue(neighbor)
return False
2.2 案例应用:迷宫最小步数
起点:1 1
终点:4 3
地图:0代表障碍物,1代表通道
1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0
求到达目标点的最小步数
2.2.1 BFS算法C++代码
#include<cstdio>
#include<queue>
using namespace std;
int start_x,start_y,end_x,end_y,width,height,step=0,min_step=9999;
int map[100][100],mark[100][100];
int direction[4][2]={{1,0},{0,-1},{-1,0},{0,1}};
struct Point
{
int x;
int y;
int step;
};
queue <Point> point;
int main()
{
scanf("%d%d",&height,&width);
scanf("%d%d%d%d",&start_x,&start_y,&end_x,&end_y);
for(int i=1; i<=height; i++)
for(int j =1; j<=width; j++)
scanf("%d",&map[i][j]);
//BFS
Point start;
start.x = start_x;
start.y = start_y;
start.step = step;
point.push(start);
mark[start_x][start_y] = 1;
while(~point.empty())
{
int x = point.front().x;
int y = point.front().y;
int step = point.front().step;
if (x == end_x && y == end_y)
{
min_step = step;
break;
}
for(int i=0; i<4; i++)
{
int temp_x = x+direction[i][0];
int temp_y = y+direction[i][1];
if (temp_x <1 || temp_y < 1 || temp_x>height || temp_y>width)
continue;
if(map[temp_x][temp_y] == 1 && mark[temp_x][temp_y] == 0)
{
Point temp_point;
temp_point.x = temp_x;
temp_point.y = temp_y;
temp_point.step = step + 1;
point.push(temp_point);
mark[temp_x][temp_y] = 1;
}
}
point.pop();
}
printf("%d",min_step);
return 0;
}
3. DFS与BFS的比较
-
性质:DFS是一种深度搜索,BFS是一种广度搜索。
-
搜索顺序:DFS沿着一条路径深入,然后回溯;BFS逐层扩展搜索。
-
解决问题:DFS适用于找到路径、拓扑排序等问题,而BFS适用于找到最短路径、连通性问题。
-
存储开销:DFS通常比BFS具有更小的存储开销,因为它只需要存储当前路径上的节点。
-
时间复杂度:在某些情况下,DFS可能需要更多的时间来找到解决方案,因为它可能会先陷入一个深度较大的分支。
4. 共同缺点
基本的深度优先和广度优先算法执行无信息搜索。它们会穷举地搜索树或图中的节点。他们不估算到达目标的特定路线的成本。当他们第一次找到目标时,他们会停下来。他们不一定能找到通往目标的最短路径。
5. 结论
深度优先搜索算法和广度优先搜索算法是解决各种问题的有力工具。选择使用哪种算法取决于问题的性质和要求。理解这两种算法的原理和特点,以及使用伪代码来帮助理解它们的实现细节,有助于我们更好地应用