⛄一、PSO-DELM简介

1 DELM的原理
在2004年，极限学习机（extreme learning machine,ELM）理论被南洋理工大学的黄广斌教授提出，ELM是一种单隐含层前馈神经网络（single-hidden layer feedforward neural network,SLFN）算法。它与常用的BP神经网络相比，ELM是对于权重和阈值随机的选取，而不像BP是通过反向传播算法调节各层之间的权值和阈值，从而减少了算法模型的学习时间和结构的复杂性，提高了模型整体的训练速度。

ELM的基本结构如图1所示，其由输入层、隐含层、输出层这3部分组成。原理说明如下，假设输入数据的样本集合为：X=xi|{1≤i≤N}，输出数据的样本集合为：Y=yi|{1≤i≤N}，其中N为样本总个数、xi为输入样本的第i个训练样本、yi为输出样本的第i个输出样本。这里设置隐含层的神经元个数为J个，则H={hi|1≤i≤J}为隐含层的输出向量的集合，hi为第i个输入样本对应的特征向量。把输入的样本数据在空间上映射到隐含层特征空间上，其二者的关系为

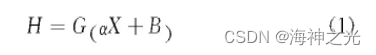
式中：G为激活函数，主要应用的有Sigmoid、Sin、Hardlim等等；α为输入层各个节点到隐含层各个节点的输入权重矩阵；B为隐含层各个节点的阈值矩阵。

图1 ELM的结构
若单隐含层的ELM能够实现在误差极小的情况下逼近“输出的N个样本”，则隐含层的输出为

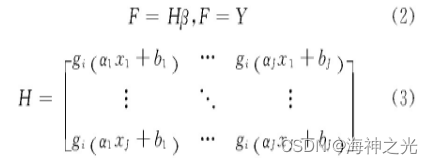
式中：β为隐含层各个节点到输出层各个节点的输出权重矩阵；H为隐含层输出矩阵。

从以上说明中能看出极限学习机的目的就是让模型的输出与实际的输出之间的差值最小，即求解输出权重矩阵的最小二乘解的问题，只要模型能够输出权重矩阵的最小二乘解就可以完成模型的训练，输出权重矩阵β可由下式表示为
由 于ELM为单隐含层结构，在面对数据量过大、输入数据的维度过高的输入输出变量时，单隐 可能会使得部分的神经元成为无效的神经元，减弱算法模型对数据特征的学习能力。在研 点。 中：C为正则化系数。

本文 高ELM-AE的泛化能力。在ELM-AE产生正交的随机权重和阈值为

式中：I是单位矩阵。

图2 ELM-AE结构
在ELM-AE中，输出权重β负责学习从特征空间到输入数据的转换。并且在传统的方法中，是根据最小二乘法求得权重系数，但是在隐含层节点数过多的情况下，这样会导致模型的泛化能力弱和鲁棒性差。所以在求解权重系数中引入正则化系数，提高模型的泛化能力，这里将目标函数设置为

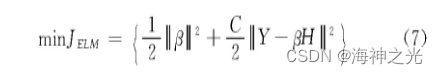
式中：C为正则化参数。对于稀疏和压缩的ELM-AE表示，把公式中的β求导，并且让目标函数为0，这样求得输出权重β为
式中：H为ELM-AE的隐含层输出矩阵；X为ELM-AE的输入和输出。

对于输入维度等于编码维度的ELM-AE,ELM-AE的输出权重矩阵β代表着从输入特征空间的数
并且在DELM中ELM-AE能用奇异值（SVD）来表示其特征，所以式（5）的奇异值分解为

深度极限学习机从结构上看相当于把多个ELM连接到了一起，但它相对于ELM能更全面地捕捉到数据之间的映射关系并提高处理高维度输入变量的精确度。DELM是逐层通过ELM-AE进行无监督的训练学习，最后接入回归层进行监督训练。其DELM的结构如图3所示，假设模型有M个隐含层，将输入数据样本X根据ELM-AE理论得到第一个权重矩阵β1，接着得到隐含层 的特征向量H1。以此类推，能够得到M层的输入权重矩阵βM和隐含层的特征向量HM。并且模型的前期是进行多层无监督的学习，不需要人为设置输入的权重和阈值，只要设置各层的隐含层的神经元个数，所以DELM拥有的学习过程快且泛化能力强的特点。

图3 DELM结构

⛄二、部分源代码

clear;clc;close all;
%% 导入数据
load data
%训练集——400个样本
P_train=input(:,(1:550));
T_train=output((1:550));
% 测试集——200个样本
P_test=input(:,(250:350));
T_test=output((250:350));
%% 归一化
% 训练集
[Pn_train,inputps] = mapminmax(P_train,0,1);
Pn_test = mapminmax(‘apply’,P_test,inputps);
% 测试集
[Tn_train,outputps] = mapminmax(T_train,0,1);
Tn_test = mapminmax(‘apply’,T_test,outputps);

%所有的数据输入类型应该为 N*dim，其中N为数据组数，dim为数据的维度
Pn_train = Pn_train’;
Pn_test = Pn_test’;
Tn_train = Tn_train’;
Tn_test = Tn_test’;

%% DELM参数设置
ELMAEhiddenLayer = [2,3];%ELM—AE的隐藏层数，[n1,n2,…,n],n1代表第1个隐藏层的节点数。
ActivF = ‘sig’;%ELM-AE的激活函数设置
C = inf; %正则化系数
%% 优化算法参数设置：
%计算权值的维度
dim = ELMAEhiddenLayer(1)*size(Pn_train,2);
if length(ELMAEhiddenLayer)>1
for i = 2:length(ELMAEhiddenLayer)
dim = dim + ELMAEhiddenLayer(i)*ELMAEhiddenLayer(i-1);
end
end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]周莉,刘东,郑晓亮.基于PSO-DELM的手机上网流量预测方法[J].计算机工程与设计. 2021,42(02)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除