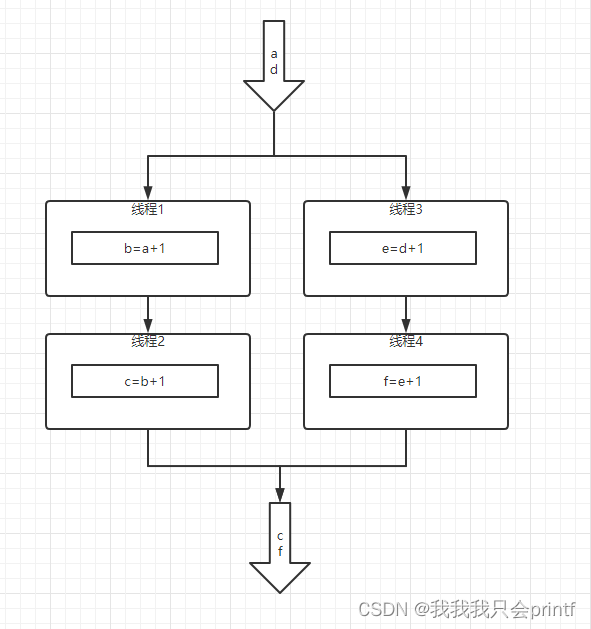
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法

对于给定的训练数据集，首先基于特征条件独立假设学习输入 / 输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y

朴素贝叶斯法实现简单，学习和预测的效率都很高，是一种常用的方法

朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型

一.贝叶斯定理

贝叶斯思维：先验概率 → 调整因子 → 后验概率

1.条件概率

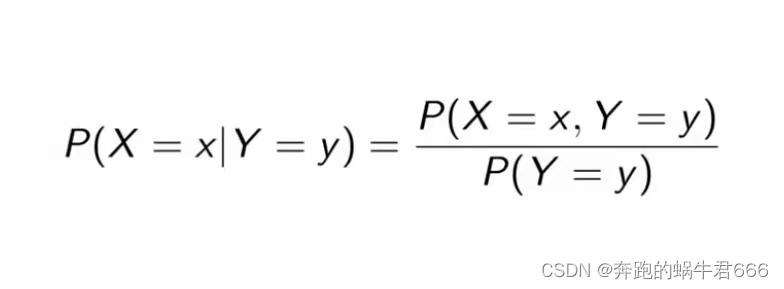2.贝叶斯定理

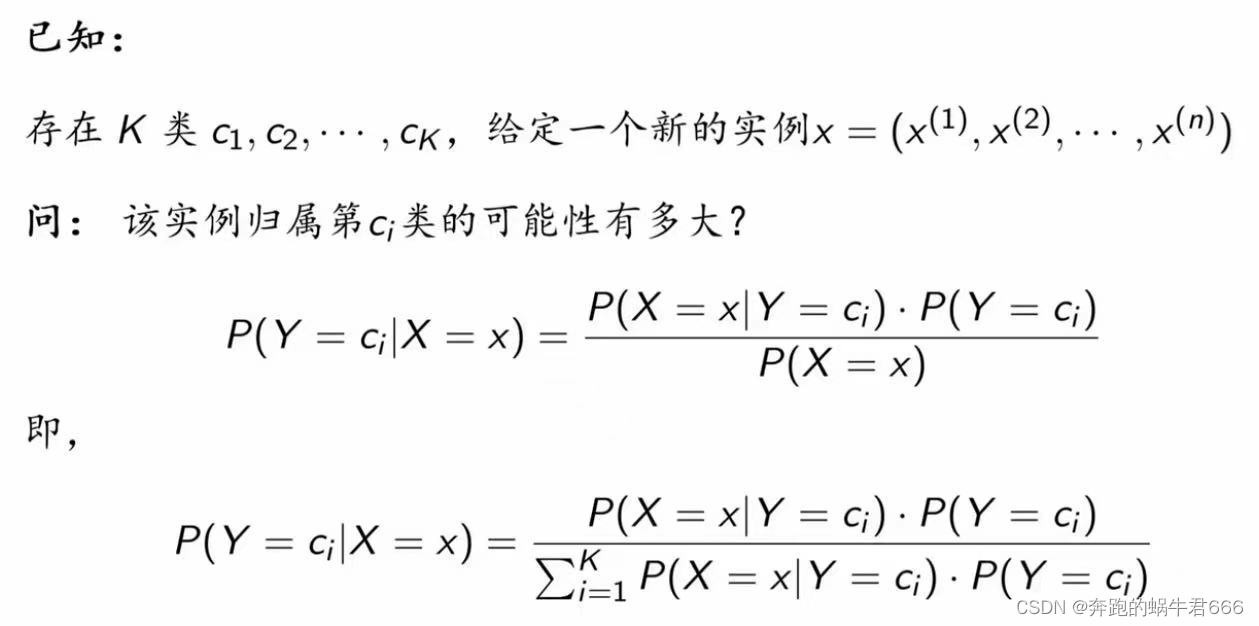3.朴素贝叶斯

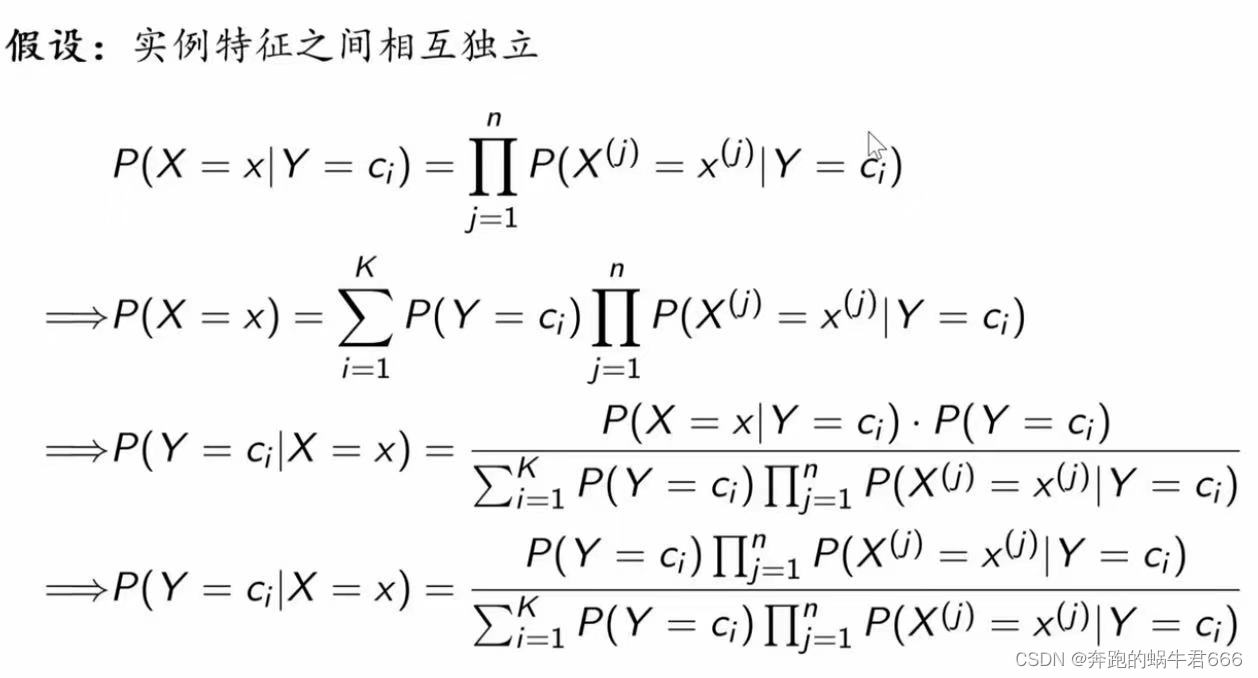二. 基本方法

1.“朴素” ？

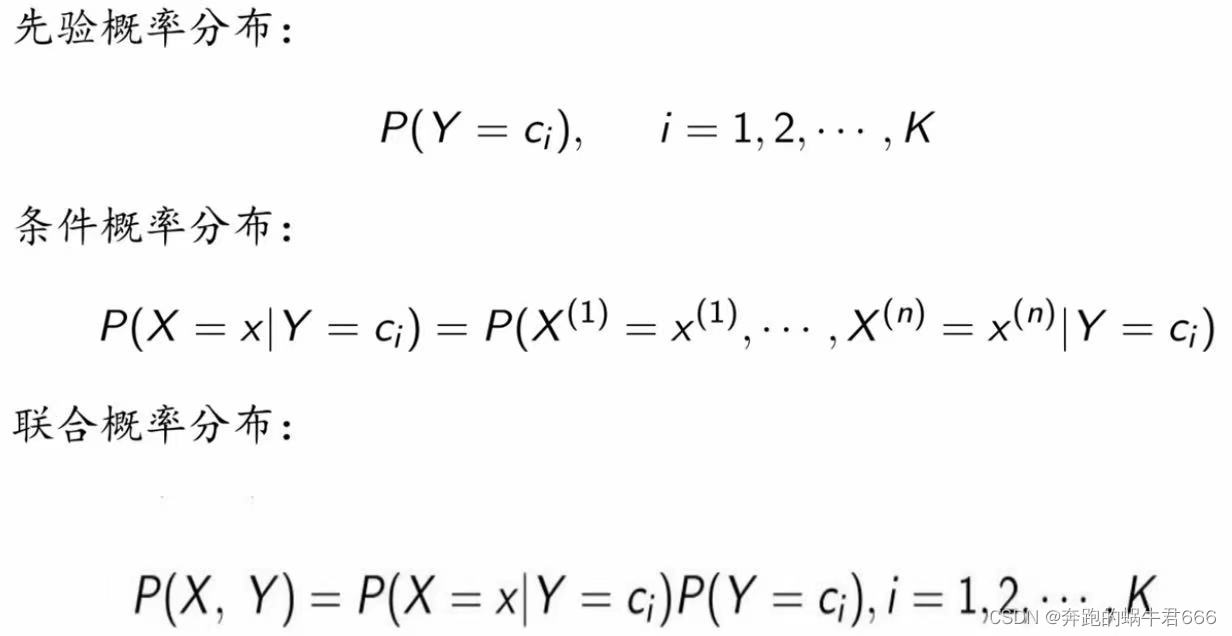
2.后验概率最大化 

 

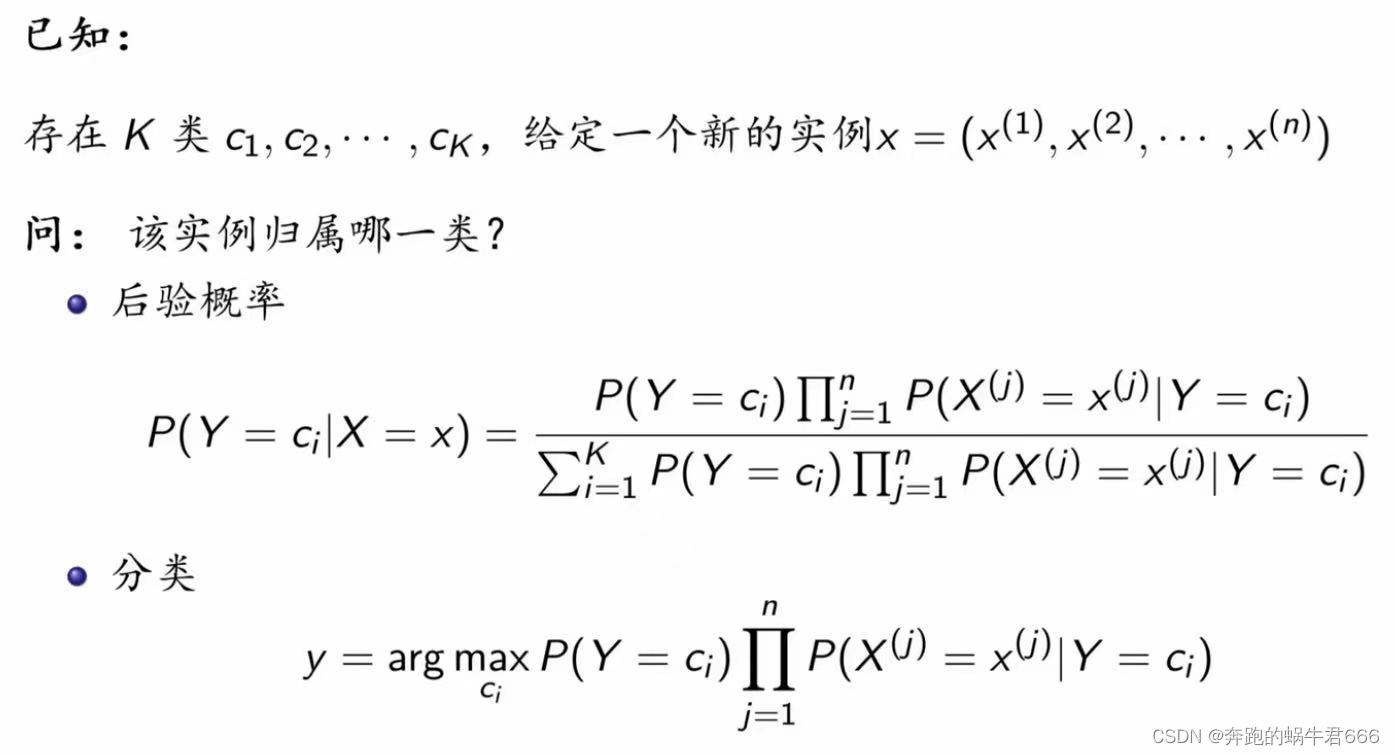
准则

期望风险最小化 → 后验概率最大化

三.极大似然估计 

1.原理

使似然函数（即联合密度函数）达到最大的参数值

2.实现

①数值计算

②迭代 

遍历 → 解析解 → 迭代法

四.算法

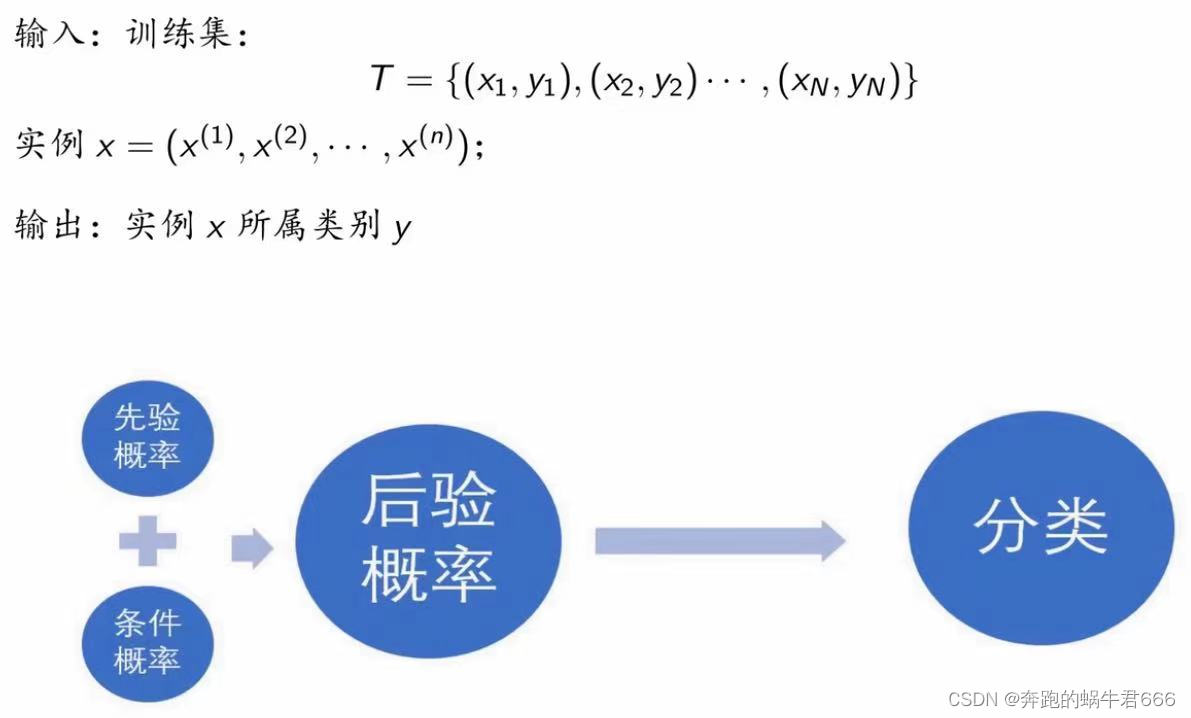五.贝叶斯估计 

平滑思想

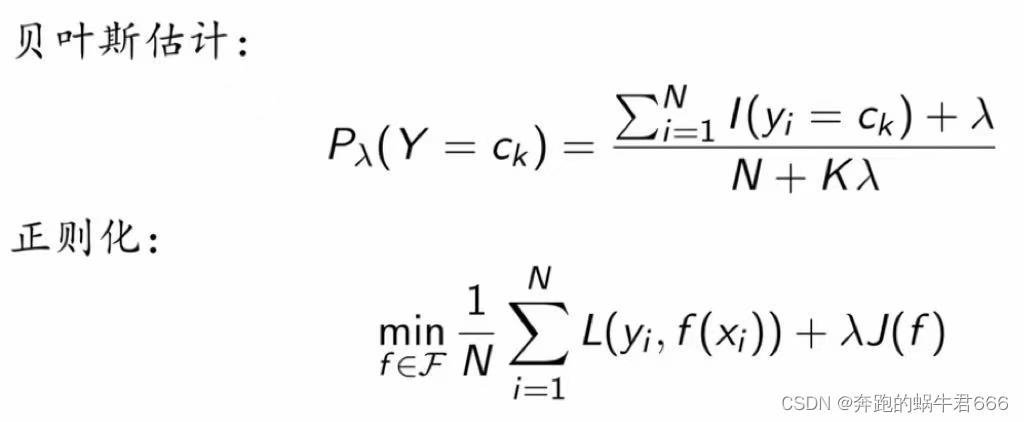
六.Python实现 

GaussianNB 高斯朴素贝叶斯

特征的可能性被假设为高斯

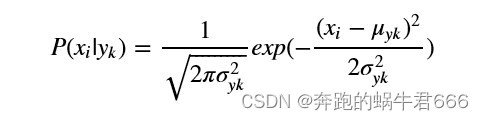
class NaiveBayes:
    def __init__(self):
        self.model = None

    # 数学期望
    @staticmethod
    def mean(X):
        return sum(X) / float(len(X))

    # 标准差（方差）
    def stdev(self, X):
        avg = self.mean(X)
        return math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))

    # 概率密度函数
    def gaussian_probability(self, x, mean, stdev):
        exponent = math.exp(-(math.pow(x - mean, 2) /
                              (2 * math.pow(stdev, 2))))
        return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent

    # 处理X_train
    def summarize(self, train_data):
        summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
        return summaries

    # 分类别求出数学期望和标准差
    def fit(self, X, y):
        labels = list(set(y))
        data = {label: [] for label in labels}
        for f, label in zip(X, y):
            data[label].append(f)
        self.model = {
            label: self.summarize(value)
            for label, value in data.items()
        }
        return 'gaussianNB train done!'

    # 计算概率
    def calculate_probabilities(self, input_data):
        # summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
        # input_data:[1.1, 2.2]
        probabilities = {}
        for label, value in self.model.items():
            probabilities[label] = 1
            for i in range(len(value)):
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(
                    input_data[i], mean, stdev)
        return probabilities

    # 类别
    def predict(self, X_test):
        # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label = sorted(
            self.calculate_probabilities(X_test).items(),
            key=lambda x: x[-1])[-1][0]
        return label

    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right += 1

        return right / float(len(X_test))

model = NaiveBayes()
model.fit(X_train, y_train)