目录
前言
国内外研究现状
细节差异分析相关研究
三维点云的相似性相关研究
存在的问题
三维点云对比的相关技术
2.1 三维点云的采集设备
2.2三维点云的存储格式
2.3三维点云的空间变换
2.4三维点云相似度分析
2.4.1点云特征的提取
2.4.2特征相似度计算
本文篇幅较长,分为上中下三篇,文章索引详见
从全局到局部的三维点云细节差异分析
从全局到局部的三维点云细节差异分析(中)
从全局到局部的三维点云细节差异分析(下)
前言
工业自动化生产是国民经济中制造业的重要组成部分,我国是制造业大国,随着
全球化的发展与制造技术的不断提升,工业制造自动化成为未来的趋势。近年来,工
业流水线制造替代了传统手工制造,自动拼装、三维打印等现代制造技术不断普及,
大大提高了生产制造效率。而在自动化带来效率提升的同时,质量检测成为一个亟待
解决的问题。在质量检测中,瑕疵检测往往通过复杂的成像技术和检测技术来进行检
测,这种流程往往计算开销大,且针对不同的工业生产线,需要定制不同的方案。
随着计算机技术的普及与发展,计算机视觉技术的研究越来越广泛。通过电子摄
像头获取到的数字图像经过分析后应用在图像识别、瑕疵检测、细节验证等方面。近
年来三维图形颇受重视,三维模型的数据也急剧增长。三维模型一般由三维图形扫
描设备扫描或三维建模软件绘制得到,具有丰富的立体表现和三维场景信息,相比于
二维图像具有更丰富的视觉感知,成为了继数字图像、语音、视频之后又一新兴数字
多媒体媒介,并在医疗、化学、生物、计算机、建筑工程等领域广泛应用。在工业生
产中,设计者使用图形设计软件进行三维物体的原型设计,为工业化生产和三维打印
提供基础原型,也可以利用三维扫描仪通过色彩相机与红外相机或雷达传感器结合,
将真实场景中的物体,以三维图形的形式存储成数字格式。在后续的流水线作业中,
为了检验生产的产品是否符合标准,需要复杂的检测流程进行产品的质量检测。现有
的三维物体表面质量检测算法体系,往往针对每一种应用场景都有特定的算法流程,
没有能够应对任意物体的普适性算法。因此可以将物体的表面质量检测问题转换为
三维刚性物体的细节差异分析问题,并基于三维点云特征提取的方式设计算法。
传统的三维物体差异对比问题,一般通过计算物体相似度来解决。然而,大多
数研究三维物体识别或检索的方法中相似度的计算只注重两个物体间的整体相似度,
忽略了局部细节差异。而描述三维物体局部细节的局部特征,则是通过局部邻接关
系、表面曲率刻画三维物体的细节信息。现有的三维物体的局部特征计算往往复杂度
较高,且主要是针对遮挡和物体不完整等问题设计的各种抗遮挡的算法,这些特性在
对比两个完整物体并进行细节差异检测时并不重要。而且,有的算法的适用对象是非
刚性物体,不能直接应用于刚性物体的细节差异分析。同时现有特征提取工作大多针
对于三维物体的三角网格结构,直接应用于点云数据的较少。相比于三角网格结构,
点云数据更容易获取,且网格结构可以快速便捷地转换为点云结构。因此,一种专门
针对刚性三维物体且只依赖于基本的点云数据的细节差异分析通用算法亟待被提出。
国内外研究现状
本文主要对细节差异对比任务进行研究,并从三维点云的全局整体形状到局部
细节实现差异分析。由于细节差异分析结果主要通过相似性分析展现,因此在本节
中,主要介绍了细节差异分析的相关研究和三维点云的相似性分析相关研究。
细节差异分析相关研究
细节差异分析主要应用于质量检测和伪造鉴别任务中。质量检测中的表面缺陷
检测主要依靠机器视觉与计算机视觉的手段来进行检测,实现对缺陷的定位、检测
及分割。表面缺陷检测是工业生产质检中的重要步骤,传统视觉方法进行处理时,一
般包括图像采集、预处理、图像分割、特征提取与识别等步骤
[1]
。这些传统的表面缺
陷算法采用手工提取特征,然后对比提取到的特征进而判断是否存在缺陷。通常使
用
Canny
边缘检测提取边缘信息
[2]
,然后分割出目标区域,再人为定义缺陷的形式和
判断规则,提取这一区域的特征,最后使用如支持向量机(
Support Vector Machines,
SVM
)等方法进行判别分析。其中,特征提取主要依据颜色直方图、尺度不变
SIFT
特征
[3]
、
SURF
特征
[4]
等,也可以根据不同类型的待检测物体手工设计特征。这种基
于传统方法的缺陷检测没有统一的方法流程,不同的缺陷类型需要进行不同的算法
设计,开发成本较高。为了提升系统性能的鲁棒性,一些基于机器学习和深度学习的
方法被提出。在无监督学习中,姚等人利用了鲁棒
PCA
的方式对太阳能电池进行缺
陷检测
[5]
,而
Huang
等人利用纹理先验和低秩表示稀疏编码的方法进行低秩重建和
缺陷检测
[6]
。自编码器也被用于识别晶圆的表面缺陷,用于建立缺陷特征的非线性
表达
[7]
。而基于深度学习的无监督学习主要依靠生成对抗网络进行缺陷检测,
Wang
等人采用自适应平衡的生成对抗网络解决类别不平衡问题,并生成模拟真实的晶圆,
通过对比生成数据与真实数据进行缺陷检测
[8]
。在有监督学习中,早期的工作主要基
于感知机或
K
近邻算法进行表面缺陷检测
[9]
,或者设计
SVM
的复杂核函数来解决问
题
[10]
。随着有监督深度学习在目标检测领域取得重大成就,基于
Faster RCNN
及其
改进版本的目标检测方法
[11]
被大量应用于缺陷检测,如轮胎缺陷
[12]
、隧道缺陷
[13]
和
光伏电池缺陷
[14]
等。
然而,这些工作主要依赖于二维图像进行缺陷检测,缺少了三维信息和空间信
息。而三维点云提供了完整的空间信息,同时兼具颜色和纹理等色彩信息。付国平等
人利用三角剖分技术实现了基于散乱三维点云的孔洞表面缺陷的检测
[15]
。郭杰利用
设计的点云局部特征进行受电弓的缺陷检测
[16]
。李坤等人利用点云配准的相关技术
进行船体的缺陷检测
[17]
,通过粗匹配和精匹配完成点云配准,并基于
KDTree
搜索
得到误差并检测缺陷。现有的三维缺陷检测手段比较有限,仍有较大的探索空间。
除了缺陷检测,伪造鉴别任务也同样依赖于细节的差异分析。刘等人利用灰度共
生矩阵进行纹理描述,提出了一种基于纹理特征识别的国徽图像鉴伪方法
[18]
。马等
人利用了文字的形态、分布和角度特征,提出了一种自适应特征融合的方式进行签名
的鉴伪方法
[19]
。然而这些方法主要通过二维图像鉴别真伪,利用三维数据进行伪造
鉴别的工作较少。
三维点云的相似性相关研究
三维点云的相似性分析有两种主要的方式:基于点云的特征对比的方法和基于
点云匹配的方法。
基于特征对比的方法是先提取点云的特征,再直接对比两个点云间特征的相似
度进行物体的识别或检索。其中,基于局部特征对比的方法使用局部的相似度来识别
物体,如
Guo
等人总结了局部特征的提取方法和用于点云识别或检索的流程
[20]
。也
有许多工作基于点云的全局特征对比进行物体的识别或检索,利用特征直方图或者
对局部特征全局汇聚得到一个全局表示的特征向量。但全局特征是对物体的整体描
述,对三维模型的细节描述不足,对整体形状相似的物体识别和描述效果欠佳。这些
特征对比的方法往往会受到点云密度变化、数据分布变化等影响,且仅能捕获三维模
型的一些关键点信息,不能对所有细节进行充分对比。
基于点云匹配的方法,则通过求解两个点云间坐标系的变换矩阵,将两个点云进
行坐标系统一和对齐后,再进行局部相似性描述。其核心在于如何求解两个点云间
的刚性变换关系。最经典的点云配准工作为
Besk
和
Mckey
提出的最近邻点迭代方法
(
Iterative Closest Point
,
ICP
),它迭代地估计了两个点云之间的变换矩阵,并不断修
正
[21]
。这个方法也被广泛应用到三维成像、机器视觉和场景重建中。虽然
ICP
简洁
有效,但存在容易陷入局部最优点的缺陷,对源点云和目标点云的初始姿态要求较
高,对于初步匹配好的点云有较好的效果,而对于刚性变换姿态差异较大的两个点
云效果欠佳。后续一些工作为了避免陷入局部最优解,采用基于全局配准的方法,此
类方法可以分为分支定界(
Branch and Bound, BnB
)和点对点(
Point and Point
,
PnP
)
关系两类。
在分支定界的方法中,具有代表性的是
Go-ICP
方法,此方法首次完成了在
ICP
框架下的全局最优配准,它用一个不确定球来表示几何边界,并根据其给出了 ICP
代价最小值下界
[22]
。
Go-ICP
根据外部
BnB
在旋转空间中搜索和内部
BnB
在几何空
间搜索迭代寻找最优解。也有一些工作利用高斯混合模型(
Gaussian Mixture Models
,
GMM
)来进行分支定界
[23]
,或者利用不对称点匹配将配准问题转换成凹二次分配问
题在
BnB
框架中求解
[24]
。虽然这些基于
BnB
的算法能够在一定程度上找到全局最
优解,但开销较大,极为耗时,难以实际应用。
在点对点关系的方法中,大部分是依赖局部特征匹配建立的点与点匹配关系来
进行求解。这类方法通常需要在源点云和目标点云中分别进行关键点检测,在检测出
的关键点上,提取局部特征,给出关键点的特征描述子并建立点对点匹配关系。然后
根据一致性检验(
RANSAC
)等筛除方法剔除误匹配并估计变换矩阵
[25]
。基于
PnP
关系的匹配方法与基于
BnB
方法相比,效果更佳,稳定性更强,速度更快,是目前
点云配准的标准方案。在
BnB
关系中,特征匹配是一个关键步骤,在二维和三维视
觉中都很受重视。在二维视觉中,
Leordeanu
等人提出了谱分析方法,构建特征点之
间的邻接矩阵,并根据邻接矩阵特征值进行匹配聚类
[26]
。
Torresani
等人通过最小化
匹配代价和能量函数来对匹配进行打分
[27]
。这些基于图匹配的方法的拓展性都不强,
Lowe
通过计算最小与次小匹配之间特征距离的比率来进行过滤筛除,有效解决了重
复模式造成的匹配二义性,但同时匹配的正确率略低
[3]
。在三维视觉中,还拓展了基
于几何刚性变换的一致性约束等方法来约束匹配。
Tombari
等人提出了三维霍夫变换
(
3D Hough Voting
,
3DHV
)来将特征匹配投影到一个三维参数空间中,并在参数空间
通过核密度极值点来确定匹配
[28]
。
存在的问题
现有的三维特征提取方法大多在三维网格数据上进行特征的提取,或基于纹理
数据进行特征计算,对采集设备的要求较高。相比于网格结构,点云数据更容易获
取,更为通用。所以本文选取了点云数据作为输入数据。而现有基于点云的相似度分
析方法,往往只关注整体的相似程度而忽略了局部细节的对比,例如三维点云检索和
三维点云识别。一些研究利用局部特征对比的方法进行物体的识别,也并没有将所有
的细节点都考虑进去。物体的细节差异分析旨在找出两个物体的每一处不同,现有的
研究工作难以直接应用。基于点云配准再对比的方法能够解决上述问题,但现有的点
云配准流程如
ICP
,依赖于较好的全局初始位置,而在实际应用中难以满足。基于特
征点匹配的点云配准方法利用局部位置的对应关系和随机抽样一致性进行点云配准,
效果较好。但直接使用点云配准来求解问题的计算复杂度较高,对于整体形状差异
较大的物体也无法实现配准。且现有的局部特征计算方法主要解决有遮挡匹配问题,
而对两个物体进行细节差异分析时并不存在这种问题,需要对这种特定场景设计新
的局部特征计算方法,以提高计算效率并提升准确率。
三维点云对比的相关技术
本章首先介绍了三维点云的采集与存储方式,接着阐述了三维点云变换的相关
知识,然后介绍了三维点云特征提取的一些常用方法以及特征相似程度的衡量手段,
最后阐明了本文研究三维点云细节差异的主要目的。
2.1 三维点云的采集设备
为了突破二维图像表达信息的局限性,人们将目光转向了三维空间,三维成像设
备日益受到关注和应用。三维扫描仪是一种以精密光学为基础的动态测量系统,用
于创建物体几何表面的点云,形成物体的表面形状,点云越密集,创建的模型就越精
确。若结合彩色相机使用,扫描仪能够获取物体的表面颜色数据,则可以进一步在重
建的表面上进行贴图,得到彩色点云和纹理图。由于三维扫描仪的扫描范围有限,因
此常需要调整扫描仪角度多次扫描以获取物体的完整模型。常见的三维成像设备依
据操作方式的不同可分为手持三维扫描仪、便携三维扫描仪以及大型固定三维扫描
仪,同时根据扫描的物理原理不同,可分为基于激光三角测量的扫描仪、三维结构光
扫描仪、接触式扫描仪等。


基于激光的
3D
扫描仪使用三角测量的过程来准确地将
3D
形状捕获为大量的点。
其工作原理是将一条或多条激光线投射到一个物体上,然后用一个或多个传感器获
取反射光线,通过计算激光的反射角从而实现精确的点位置测量。除了用于小型物体
扫描,三维激光扫描仪也是地形测绘、土木勘测的重要测量工具。基于激光的三维扫
描仪通常较为便携,如手持便携扫描仪、单臂扫描仪等。利用激光三角测量原理进行
三维扫描,对于一些坚硬的表面、深色的平面扫描效果较好,对变化的光照条件和环
境光不敏感,且设备相对廉价。图
2.1
展示了市面上常见的由
Go3Dpro
公司研制的
EinScan H
手持激光三维扫描设备。
三维结构光扫描仪使用蓝色或白色的
LED
投射光,将由条状、块状或其他形状
组成的光图案投射到物体上,然后利用一个或多个传感器,查看这些图案或结构形状
的边缘以确定对象的三维形状,同时结合三角测量的原理使得测量更加精确。结构光
3D
扫描仪的精度极高、扫描速度极快、噪声少、分辨率高,但只能适用于中短距离
物体,且便携性较低、价格较高。图
2.2
展示了市面上常见的由
Artec3D
公司研制的
Artec Eva 结构光三维扫描设备。


接触式三维扫描仪采用实际触碰物体表面的方式来计算深度,如座标测量机。这
种方法精确度很高,经常在工程制造产业中使用,然而因其在扫描过程中必须接触物
体,待测物有遭到探针破坏损毁之可能,因此不适用于高价值对象如古文物、遗迹等
的重建作业。此外,与其他方法相比扫描需要的时间会更长。
2.2三维点云的存储格式
三维对象的基本数据结构包括点、面、法向量、纹理、颜色、光照等多种信息,
而点云作为三维对象最主要的信息,一般包含点的空间位置坐标、点的法向量信息和
点的颜色信息。三维点云的存储一般使用标准的点云存储文件结构或三维对象存储
结,常用的文件类型有
obj
、
off
、
ply
、
xyz
、
pcd
、
las
、
stl
等。
obj
格式是由
Wavefront Techonologies
公司提出的一种文件结构,其从几何学上
定义三维模型的结构,属于文本文件结构。文件头通常是以‘
#
’开始的注释行。数
据部分,每一行的开头关键字代表该行数据所表示的几何和模型元素,用空格来分隔
数据。对于点云数据来说,其中最基本的关键字是
v
顶点,也可以存储法向量和颜色
等信息。
obj
格式除了能够存储基本的点云数据外,还能够存储面、纹理、光照等复
杂的三维信息,是一种广泛应用在三维制图、
CAD
等领域的通用文件结构。
与
obj
格式文件相比,
off
文件存储格式更为简单。
off
是一种文本格式,文件头
有两行,其中第一行以
off 关键字开头,第二行则表示了顶点数、面数、边数。主体
分为顶点坐标(顶点列表)和面的顶点索引(面列表)两个部分,其中可以指定每个
面的顶点数,用第一个数表示。
off
格式存储了点云基本信息和面结构信息,是比较
简洁通用的存储格式,
ModelNet
数据集即采用
off
的文件格式进行存储
[29]
。
ply
由斯坦福大学的
Turk
等人设计开发,是一种多边形文件格式,也可以称之为
斯坦福三角格式。文件格式分为文本和二进制两种格式。文件包含头部信息、顶点列
表和面列表以及其他信息的列表,然后是按照列表格式呈现的数据段。该文件结构同
样能够存储点云基本信息和面的基本信息,是常用的点云存储文件结构,后文用到的
Stanford Models
数据集即采用
ply
的格式进行存储
[30]
。图
2.3
展示了真实的
ply
文件
存储信息,包含头结构和基本数据段。


xyz
是一种文本格式,前面
3
个数字代表点坐标,后面
3
个数字表示点的法向量,
用空格将数字分隔,也可以再增添
3
个数字表示点的颜色。该文件结构相比于其他结
构而言,具有更简洁的存储格式,但仅能够表示最基本的点云数据,不能存储面、纹
理、光照等复杂的三维信息。
pcd
是
PCL
点云库的官方指定格式,典型的为点云量身定制的格式。优点是支
持
n
维点类型扩展机制,能够更好的发挥
PCL
库的点云处理性能。文件格式包含文
本和二进制两种类型。
pcd
格式具有文件头,用于描绘点云的整体信息。数据本体部
分由点的笛卡尔坐标构成,文本模式下以空格作为分隔符。但该存储类型与其他的三
维处理软件如
MeshLab
等兼容性不高,存在使用局限性。
las
是激光雷达(
LiDAR)数据的工业标准格式,是一种二进制文件格式。目的
在于提供一种开放的格式标准,允许不同的硬件和软件提供商输出可以互操作的统
一格式。该文件格式主要支持激光雷达数据的存储,普适性较低。
stl
是
3D Systems
公司创建的三维模型文件格式,用于表示三角形网格,主要在
CAD
、
CAM
领域中应用。
stl
分为文本和二进制两种格式。文本格式的
stl
文件在首
行中给出了文件路径及文件名,然后逐行给出三角面片的几何信息。二进制格式以三
角面为单位组织数据,每一个三角面由
7
行数据组成,最后一行是结束标志。
综合以上对常用的点云存储文件类型的描述,本文主要使用简洁易用且通用性
强、兼容性高的
ply
文件格式作为点云存储格式并进行后续算法与系统的设计、开发
与实验。
2.3三维点云的空间变换
三维点云的空间变换包括刚性变换和非刚性变换。本文的研究对象主要是刚体,
因此下面主要介绍三维物体的刚性运动。三维物体的刚性运动通过刚性变换来描述,
由两个坐标系间的平移和旋转组成。可以表示为平移矩阵、旋转矩阵和欧拉角等[31]。






因为增加了缩放变换,此时就不再是刚体变换了,这种变换是相似变换,描述了
旋转、平移以及等比例尺度缩放的过程。同样地,若不要求旋转矩阵
R
的正交性,可
将
R
替换为任意可逆矩阵
A
,则可描述仿射变换。这些变换及其对应的不变性在表
2.1
中详细描述,表格中
a
描述了透视变换,
𝑣
表示整体比例因子。其中欧式变换为
刚性变换,其他为非刚性变换。


上述的三维点云空间变换的基础知识,为本文的特征匹配、尺度相似度计算等方
面提供了理论基础。
2.4三维点云相似度分析
三维点云的相似度衡量一般用于点云检索、物体识别、点云配准几个常见的任务
中。其中最广泛、最直接的应用为点云检索,检索是通过用户给定的一个三维点云模
型,从数据库中检索出最相似的若干个三维点云物体。该过程主要依靠点云间相似度
的计算来衡量相似程度。检索流程主要包括构造三维模型数据库、对数据库内的三
维模型进行特征提取并存储、读取用户输入的点云、点云预处理、计算输入点云的特
征、计算输入点云特征与数据库内点云特征的相似度、根据相似度进行排序最终显
示给用户等几个步骤。首先预定义系统的数据集,然后对数据集中的三维点云提取
点云特征,并保存在数据库内等待匹配。对于用户输入的点云,进行预处理与特征计
算,并将计算得到的点云特征与数据库存储的点云特征做对比,计算其相似度。选择
出相似度最大的若干个物体作为检索系统一次查询的输出。三维点云物体识别与检
索类似,依靠点云特征的计算,然后利用霍夫变换投票来进行物体检测,根据特征空
间的相似度将特征投票到参数空间,然后在参数空间识别物体。而基于点对点关系的
点云配准则针对于每个特征点,预定义一系列的关键点,然后在关键点计算特征描述
向量,并对比特征向量之间的相似度,确定匹配关系,然后求解变换矩阵。
在三维点云相似度计算中,主要依赖的两个核心步骤为特征的提取和特征相似
度的计算,最终给出相似度得分。
2.4.1点云特征的提取
根据三维点云特征提取算法的不同,主要分成两大类:点云全局特征和点云局部
特征。点云全局特征描述了点云整体的几何结构、颜色、空间信息等,常表达为一个
特征向量,这种表达一般需要该特征具有平移、缩放、旋转的不变性以避免歧义。全
局特征有良好的不变性,表示直观,但一般特征维数较高,计算量大,且不适用于点
云不完整有遮挡的情况。局部特征则是点云局部区域中抽取的特征,能更好地表示细
节特征,易于快速匹配。


全局点云特征提取方法根据处理方法和表现形式的不同,一般分为
[32]
:(
1
)基于
统计直方图的算法;(2
)基于多视图的特征提取方法;(
3
)基于拓扑结构的方法;(
4
)
基于集合变换的提取方法;(5
)基于深度学习的特征方法
基于统计直方图的算法一般具有简洁高效的特性,但表达能力较弱,是一种广泛
使用的统计性特征提取方式。该方法主要依靠不同的区间划分对随机信号进行统计,
对三维点云而言,一般可以通过同心球划分、扇形划分和组合划分将点云模型划分
成不同的区间,并在不同区间内分别计算一个数值特征(通常为计数)得到直方图向
量。其中同心球划分,不随点云的旋转和平移发生区间划分的变化,具有平移和旋转
不变性,而扇形划分和组合划分,会随着点云的旋转产生不同的划分结果,不具有旋
转不变性。组合划分和扇形划分将网格划分的更细致,具有较好的表现力,但不具有
旋转不变性,需要待处理点云处于同一坐标系下且方向严格对齐,约束性较高。

基于多视图的特征提取方法也是常用的一种三维特征提取方法
[33-34]
。早期的计
算机视觉主要在图像领域进行了大量研究,提出了包括
Harrs
[35]
、
SIFT
[3]
等成熟的二
维图像特征提取方法。然而,这些成熟的二维图像特征提取方法难以直接用于三维点
云,所以一种直观的想法是把三维图形投影为二维图形,认为如果两个三维模型相似,
那么两者的二维投影也应该是相似的,然后在二维图形上进行特征计算。
M2DP
[34]
和
MVCNN
[33]
这些方法都依靠此种思路,将复杂的三维点云投影到多个二维平面,然
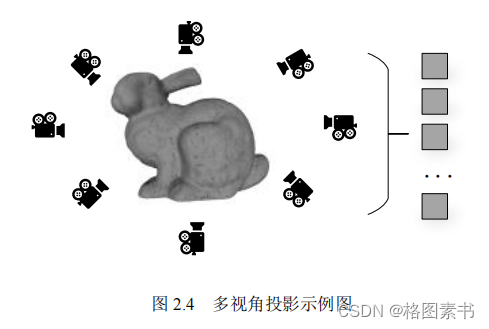
后在二维空间中提取图像特征,并将每个视图的特征整合在一起。如图
2.4
所示,三
维物体经过多视角投影,可以映射到不同二维平面上,并通过在二维图像上提取图像
特征完成点云的特征提取,并融合不同视图间的特征。这种方法计算简洁,具有直观
的可解释性。然而,这种方法高度依赖于投影平面的选择方式和投影分辨率,不同坐
标系下选择不同的投影平面,将会导致该特征存在一定的旋转歧义性,一些方法为了
弥补这个缺陷,提取了利用不同角度的上千个投影平面来提高鲁棒性,构成光场特
征,其计算效果较好,但计算复杂度高,难以进行普遍推广
[36]
。
基于拓扑结构的特征提取方法描述了三维物体内部的几何拓扑结构和结构之间
的相互关联。对于同一类物体,其拓扑结构较为相似,不同类的物体拓扑结构差异较
大,一般用于描述物体的大体形状、轮廓等特性。常见的方法有
Reeb
图
[37]
、属性邻
接图
[38]
和骨架图
[39]
等。
Reeb
图利用函数描述拓扑关系,对变形具有鲁棒性,比较适
用于非刚性物体运动描述
[37]
。属性邻接图通过图来表达拓扑结构,利用图算法进行
相似度评估。例如该方法被用作
CAD
模型的聚类表达中
[40]
。基于骨架图的描述方
法通过三维模型骨架提取方法进行骨架提取,比较直观。基于骨架的方法比较适用于
人、动物等具有关节性的物体,但并不适用于自然界的普适物体。
基于集合变换的方法一般通过频域变换的方式实现,如小波变换、傅里叶变换、
球面调和变换等利用频率描述三维物体。
Vranic 等人利用离散傅里叶变换描述了体
素化的三维模型来表达三维物体的特性
[41]
。基于球面调和变换的方法首先构造球面
函数,然后通过球面变换得到较为紧凑的特征表达。
Vranic
等人将球面调和引入三维
特征提取领域,并经过
Kazhdan
等人的改进后具有了旋转不变性
[42]
,但仍然面临着
计算较为复杂的问题。
基于深度学习的方法最初通过将三维点云转换成二维图像,然后借助图像卷积
神经网络进行特征的构建,如
MultiView CNN
[33]
,这种方法依赖于点云投影,计算
复杂且由于坐标系的不一致问题难以得到有效的特征表达。
Qi
等人提出了
PointNet
和
PointNet++
,直接使用深度神经网络对点云坐标数据进行特征提取
[43-44]
。然而,
PointNet
没有考虑点的局部关系,
Wang
等人利用动态图构建了点云网络,并在局部
进行卷积操作,提出了
DGCNN
算法,提高了点云特征的表达力
[45]
。近些年来,大
量基于图卷积的深度学习的特征提取网络被提出,并用于点云分类、分割等任务中。
近两年,利用全注意力机制的点云特征网络也被提出,如
Guo
等人提出了
PCT
网络,
利用注意力机制强大的特征表达能力,取得了点云特征表达的较好结果
[46]
。然而,当
测试场景发生较大的变化时,这些方法往往结果较差,需要额外的迁移学习或大规模
自然场景数据集的支撑,且计算复杂度较高,依赖于现代高性能计算平台。
本文的研究对象为三维的刚性物体,因此将主要对基于直方图和多视图的三维
全局特征提取方法进行研究。
局部点云特征提取方法一般分为:(
1
)针对刚体的局部特征;(2
)针对非刚体
的局部特征。其中,物体的相对位置关系在变换过程中保持不变的为刚性物体变换,
而类似人体等具有关节活动、形状改变的物体为非刚性物体。在描述局部特征之前,
应预设一组关键点表示待提取特征的局部位置,可以将点云中的所有点作为关键点,
也可以利用一些关键点定位方法自动选择有代表性的局部位置。如在
SIFT
方法
[3]
上
衍生出的
SIFT3D
关键点定位方法,利用局部颜色极值点来确定关键点位置。
Zhong
等人设计的
ISS3D
特征点
[47]
在不同视角进行计算得到关键点位置,而
Steder
等人利
用边界与前背景信息计算关键点
[48]
。
刚性变换物体的局部特征主要通过描述局部几何结构、法向量等表面信息来构
建局部特征。
Johnson
等人利用邻域点在关键点的法向量切平面投影生成旋转图像,
得到
Spin Image
特征描述子
[49]
,
Frome
等人将特征关键点作为球心构建三维球体,并
将三维球体划分成不同的空间部分,在不同的空间内统计点的信息作为关键点的三
维形状上下文描述子(
3DSC
)
[50]
。旋转投影数据描述子(
Rops
)由
Guo
等人提出,通
过构建唯一的局部参考系进行特征的计算
[51]
,后续又将
Spin Image
的思路融合到唯
一的局部参考系内,形成每个轴独立计算的
Triple Spin Image
特征描述子
[52]
。
Salti
等
人也构建了唯一的坐标系然后对三维球体划分统计每个点的法向量信息
[53]
,同样的
思路也被
Tang
等人应用进行局部特征的计算
[54]。也有一些工作统计每个点的信息,
构建点特征直方图(
PFH
)进行局部特征描述
[55]
,
但计算复杂度较高,后续经过加速
改进后,成为比较主流应用的快速点特征直方图(
FPFH
)局部特征
[56]
。基于深度学
习的局部特征方法一般也针对刚性物体,一般通过全局特征构建网络的前半部分来
构建局部点特征表达,然后专门设计基于深度学习的局部特征增强网络和匹配网络,
例如
Wang
等人提出的
DCP
[57]
和
Aoki
等人提出的
PointNetLK
网络
[58]
。
非刚性变换物体的局部特征在近几年开始被研究,主要用于姿态的估计以及物
体的识别,这类特征在非刚性变换下仍然保持不变性。早期的方法参照形状上下文的
方式,在测地距离的框架下进行局部特征的提取
Reeb
图特征
[59]
。
Lipman
等人提出
使用局部保形拓扑结构区域内的点作为特征描述对比方法
[60]
。随着研究的进展,拉
普拉斯
-
贝尔特拉米算子被提出用于几何处理
[61]
。一些基于拉普拉斯特征方程的方法
被提出
[62]
,随后,
Sun
等人又解决了拉普拉斯特征值的正负号问题
[63]
,
基于该工作,
Aubry
等人提出了更具有代表性的基于波核函数(
WKS
)的方法解决这一问题
[64]
。
然而这些局部特征大多依赖于局部的网格面片结构,而非单纯的三维点云。一些设备
进能够采集三维点云数据,而没有网格面片结构,这种情况需要首先进行表面网格结
构的估计与重建,引入额外大量计算。
本文的研究对象为刚性变换物体,对比两个刚性变换物体的细节差异才具有实
际意义,因此在后续的章节中,以针对三维刚体点云的特征提取方法为主要讨论与研
究的对象。
2.4.2特征相似度计算
点云的相似度计算,通常通过计算特征之间的相似度。特征的相似度度量一般
计算两个特征向量之间的距离,特征向量间的距离越小,其相似度越高。给定两个三

给定两个特征计算相似度,其距离应该满足交换律,不会随着顺序的变换而对结果产
生影响。正定性描述了两个特征间的距离必须大于
0
,而三角不等式性质描述了作为
描述相似度的距离度量函数需具有偏序单调性,不会产生歧义性。
常用的距离度量包括:欧式距离、曼哈顿距离、余弦相似度、杰卡德相关系数、
皮尔逊相关系数等。其中欧式距离和曼哈顿距离度量了欧几里得空间中的远近程度,
具有计算简洁高效的优点。余弦相似度将两个特征向量看作欧氏空间中的带方向向
量,然后衡量两个向量的夹角的大小,该方法常用于衡量归一化的特征或单位向量之
间的相似度,同样计算简洁高效。而杰卡德相关系数衡量了两个无需特征间的相似
度,但计算不够精确。皮尔逊相关系数用来计算两个向量的相关性或分布的相关性,
具有平移不变性和尺度不变性。