【2596. 检查骑士巡视方案】

news2025/1/22 19:01:48

来源：力扣（LeetCode）

描述：

骑士在一张 n x n 的棋盘上巡视。在有效的巡视方案中，骑士会从棋盘的左上角出发，并且访问棋盘上的每个格子恰好一次。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

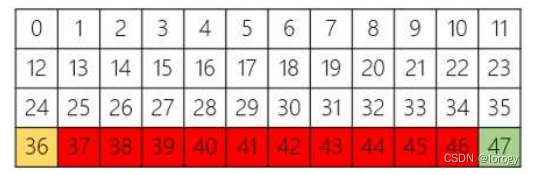
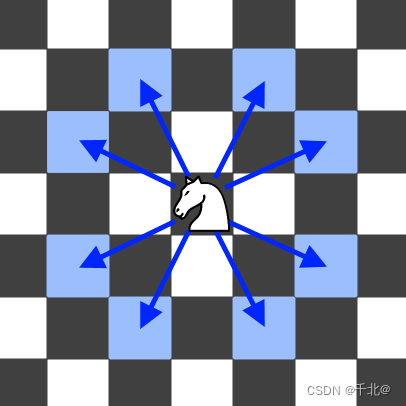
注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

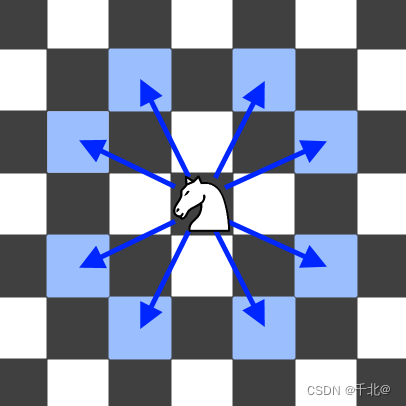
示例 1：

输入：grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
输出：true
解释：grid 如上图所示，可以证明这是一个有效的巡视方案。

示例 2：

输入：grid = [[0,3,6],[5,8,1],[2,7,4]]
输出：false
解释：grid 如上图所示，考虑到骑士第 7 次行动后的位置，第 8 次行动是无效的。

提示：

n == grid.length == grid[i].length
3 <= n <= 7
0 <= grid[row][col] < n * n
grid 中的所有整数 互不相同

方法：直接模拟

思路与算法

题目要求骑士的移动的每一步均按照「日」字形跳跃，假设从位置 (x₁, y₁) 跳跃到 (x₂, y₂)，则此时一定满足下面两种情形之一：

∣x₁ − x₂∣ = 1, ∣y₁ − y₂ ∣ = 2；
∣x₁ − x₂∣ = 2, ∣y₁ − y₂∣ = 1。

设矩阵的长度为 n，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格，因此可以知道每个单元格的访问顺序，我们用 indices 存储单元格的访问顺序，其中 indices[i] 表示骑士在经过第 i − 1 次跳跃后的位置。由于骑士的行动是从下标 0 开始的，因此一定需要满足 grid[0][0] = 0，接下来依次遍历 indices 中的每个元素。由于 indices[i] 是一次跳跃的起点，indices[i+1] 是该次跳跃的终点，则依次检测每一次跳跃的行动路径是否为「日」字形，即满足如下条件：

∣indices[i][0] − indices[i+1][0]∣ = 1,∣indices[i][1] − indices[i+1][1]∣= 2；
∣indices[i][0] − indices[i+1][0]∣ = 2,∣indices[i][1] − indices[i+1][1]∣= 1。

为了方便计算，我们只需检测 ∣x₁ − x₂∣ × ∣y₁ − y₂∣ 是否等于 2 即可。如果所有跳跃路径均合法则返回 true ，否则返回 false。

代码：

class Solution {
public:
    bool checkValidGrid(vector<vector<int>>& grid) {
        if (grid[0][0] != 0) {
            return false;
        }
        int n = grid.size();
        vector<array<int, 2>> indices(n * n);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                indices[grid[i][j]] = {i, j};
            }
        }
        for (int i = 1; i < indices.size(); i++) {
            int dx = abs(indices[i][0] - indices[i - 1][0]);
            int dy = abs(indices[i][1] - indices[i - 1][1]);
            if (dx * dy != 2) {
                return false;
            }
        }
        return true;
    }
};

时间 16ms 击败 69.53%使用 C++ 的用户
内存 27.05MB 击败 23.43%使用 C++ 的用户
复杂度分析

时间复杂度：O(n²)，其中 n 表示二维棋盘边的长度。需要检测棋盘中的每个位置，一共需要检测 n² 个位置，因此时间复杂度为 O(n²)。
空间复杂度：O(n²)，其中 n 表示二维棋盘边的长度。用来需要存放每个位置的访问顺序，一共有 n² 个位置，需要的空间为 O(n²)。
author：力扣官方题解