在part-1中，我们梳理了去中心纸牌游戏所面临的挑战，也介绍了一种改进的Barnett-Smart协议，part-2将深入了解该协议背后涉及的算法。

Discrete-log VTMF

VTMFs包含4部分：key generation, mask, remask and unmask，这些算法主要通过El Gamal加密算法来实现的。可验证性是通过零知识证明来实现的，主要用于证明加密和解密操作的正确性。

key generation

玩家i 随机选取私钥 $x_i\leftarrow Z_q$ , 计算相应公钥$H_i=x_i\cdot G$并公开（为抵抗rogue key attacks，要求每个玩家提供一个零知识证明，可以使用schnorr身份证明协议）

一旦所以玩家公开他们的公钥之后，我们可以计算一个聚合公钥$H$，其中$l$代表参与玩家总数
$$H=\sum _i^l{H}_i=\sum _{i=1}^l{x}_{i}G$$

Mask

用${\zeta }_H$表示掩码函数，$H$表示聚合公钥，$M\in G$表示卡牌映射在群G上的元素，对$M$进行mask得到密文$C\in G\times G$， 其过程如下：
$$C={\zeta }_H(M,r)=\left(\begin{array}{c}{C}_a\\ C_b\end{array}\right)=\left(\begin{array}{c}rG\\ M+rH\end{array}\right)$$

这里$r\in Z_q$被称为masking factor。通过计算$C_b-rH$ 可以恢复卡牌， 所以r必须保密不可泄漏。

Remask

用${\zeta }_H^{\prime }$表示掩码函数，$H$表示聚合公钥，玩家随机选择$r^{\prime }\leftarrow Z_q$，对掩码卡牌$C=\left(\begin{array}{c}{C}_a\\ C_b\end{array}\right)$进行重掩码：
$$C^{\prime }={\zeta }_H^{\prime }(C,r^{\prime })=C+\left(\begin{array}{c}{r}^{\prime }G\\ r^{\prime }H\end{array}\right)=\left(\begin{array}{c}{C}_a+r^{\prime }G\\ C_b+r^{\prime }H\end{array}\right)$$

例如一局游戏有Alice、Bob和Charlie三个玩家，这三个玩家先后其对卡牌进行掩码和重掩码的过程如下：Alice首先用$\alpha$去随机化卡牌M得到$C_1$，然后Bob用$\beta$对$C_1$进行重掩码得到$C_2$，最后Charlie用$\gamma$对$C_2$进行重掩码得到$C_3$。
$$\begin{array}{rl}& C_1={\zeta }_H(M,\alpha )=\left(\begin{array}{c}\alpha G\\ M+\alpha H\end{array}\right)\\ & C_2={\zeta }_H^{\prime }(C_1,\beta )=C_1+\left(\begin{array}{c}\beta G\\ \beta H\end{array}\right)=\left(\begin{array}{c}(\alpha +\beta )G\\ M+(\alpha +\beta )H\end{array}\right)\\ & C_3={\zeta }_H^{\prime }(C_2,\gamma )=C_2+\left(\begin{array}{c}\gamma G\\ \gamma H\end{array}\right)=\left(\begin{array}{c}(\alpha +\beta +\gamma )G\\ M+(\alpha +\beta +\gamma )H\end{array}\right)\end{array}$$

在所有玩家完成上述掩码或重掩码过程后，实际上我们得到在masking factor为$\alpha +\beta +\zeta$下的掩码卡牌，因此要恢复卡牌，需要每个玩家提供其所拥有的masking factor，还有另外一种方法不需要提供masking factor，见下面unmask过程。

Unmask

给定掩码卡牌$C=\left(\begin{array}{c}{C}_a\\ C_b\end{array}\right)$，玩家i使用私钥计算$D_i=x_i{C}_a$并公开，等待所有玩家公开之后，可以计算
$$M=C_b-\sum _{i=1}^l{D}_i$$

Verifiability

上述操作（不包括密钥生成）的可验证性可以通过Chaum-Pedersen离散对数相等性证明来实现。在经典的sigma协议中, 给定$\alpha G$和$\beta H$, 证明者可以通过zero knowledge证明他知道$\alpha$的值且$\alpha =\beta$ 。对于mask操作而言，需要证明和验证的是$c_a$和$c_b-M$对应$\alpha =r$ , 对于remask操作而言，需要证明和验证的是$c_a^{\prime }-c_a$和$c_b^{\prime }-c_b$对应$\alpha =r^{\prime }$ , 对于unmask操作来说，需要证明和验证的是$H_i$和$D_i$对应$\alpha =x_i$ ,

ZK Shuffle

为了便于理解ZK Shuffle，假设存在一组群中元素$P_1,P_2,...,P_N$ ,这些元素经过置换再加上盲化因子${\Delta }_i$后输出为：
$$P_i^{\prime }=P_{\pi (i)}+{\Delta }_i$$
其中$\pi$为置换函数，下面这张图展示了6个元素的置换过程：

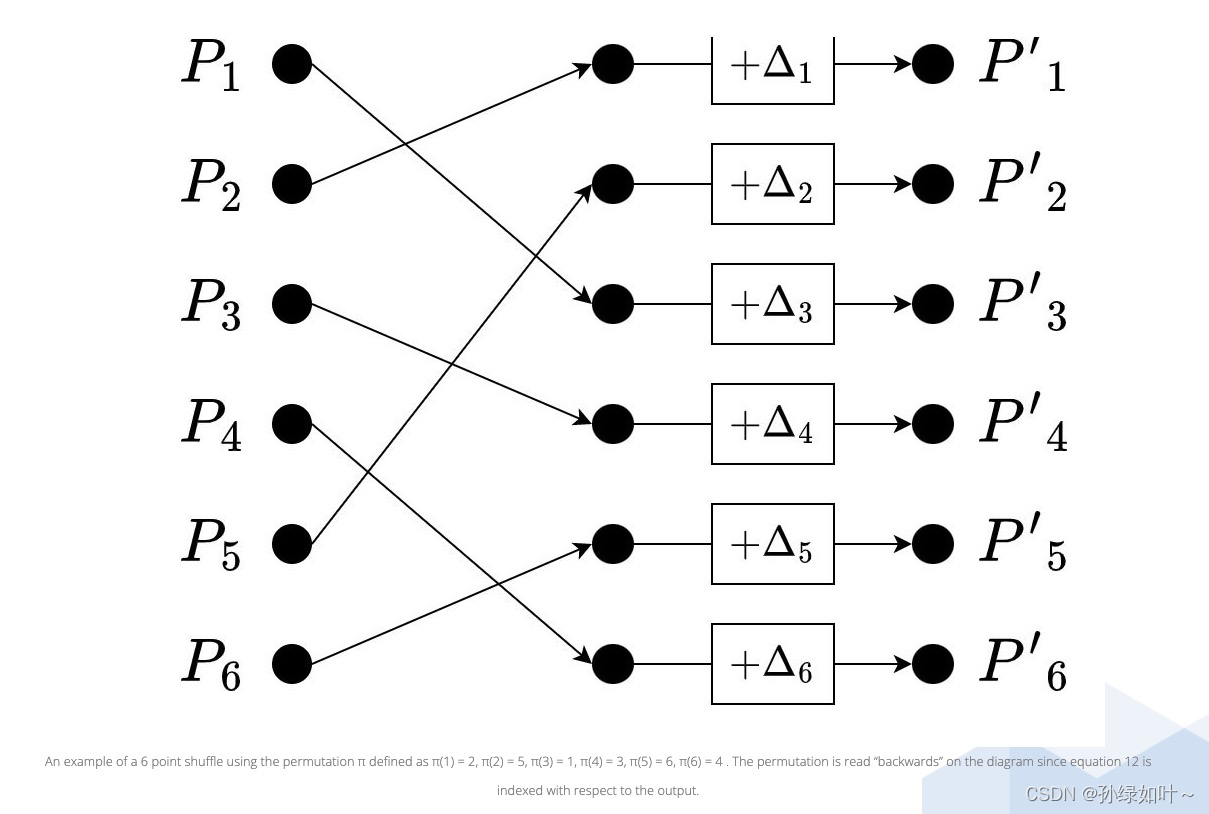
为了有效地生成论证(argument)，我们使用多项式等式来表示洗牌过程。然后，我们从domain上选择一个随机点，在该点打开多项式，并通过比较在该点的值是否相等来验证等式是否成立。其中一个多项式由验证者使用公开数据来计算，另外一个多项式由证明者使用秘密数据来计算。由于证明者不可信，还必须设计额外的arguments来确保证明者的多项式是正确计算的。

Shuffle as a Polynomial Equality

argument的核心是下面这个验证等式，给定一个挑战 z c ← Z q \ { 0 , 1 } z_c \leftarrow Z_q \backslash \{0,1\} zc​←Zq​\{0,1}，验证者验证：
$$\sum _{i=1}^N{z}_c^i{P}_i=\sum _{i=1}^N{z}_c^{\pi (i)}(P_i^{\prime }-{\Delta }_i)$$
等式左边可使用公开数据（shuffle的输入）和挑战计算，因此这部分验证者可以计算；而等式右边只能由证明者计算，因此它涉及到秘密置换$\pi$和盲化因子${\Delta }_i$。

注意到上述等式同两个多项式在点$z_c$处打开的过程非常相似。我们可以用变量乘以生成元的形式来表示上述等式中的元素：

• 令$s_i\in Z_q$，则$P_i=s_{i}G$
• 令$s_i^{\prime }\in Z_q$，则$P_i^{\prime }=s_i^{\prime }G$
• 令${\delta }_i\in Z_q$，则${\Delta }_i={\delta }_{i}G$

用这些新的形式替换上面等式，得到：
$$(\sum _{i=1}^N{z}_c^i{s}_i)G=(\sum _{i=1}^N{z}_c^{\pi (i)}(s_i^{\prime }-{\delta }_i))G$$
考虑下面的多项式$f$和$g$，这两个多项式在$z_c$处的打开值再乘以群的生成元就可以得到上面的等式：
$$f(z)=\sum _{i=1}^N{z}^i{s}_i,g(z)=\sum _{i=1}^N{z}^{\pi (i)}(s_i^{\prime }-{\delta }^i)$$
鉴于累加的顺序是可以交换的，则$f$可以写成$f(z)={\sum }_{i=1}^N{z}^{\pi (i)}{s}_{\pi (i)}$，实际上只是通过置换改变求和中每项的顺序，所以最后累加的结果不变。
f ( z ) = g ( z ) ⟺ ∑ i = 1 N z π ( i ) s π ( i ) = ∑ i = 1 N z π ( i ) ( s i ′ − δ i ) ⟺ ∀ i ∈ { 1 , 2 , . . . , N } , s π ( i ) = s i ′ − δ i ⟺ ∀ i ∈ { 1 , 2 , . . . , N } , P π ( i ) = P i ′ − Δ i f(z) =g(z) \Longleftrightarrow \sum_{i=1}^Nz^{\pi(i)}s_{\pi(i)} = \sum_{i=1}^Nz^{\pi(i)}(s_i' - \delta^i) \\ \Longleftrightarrow \forall i\in \{1,2,...,N\},s_{\pi(i)} = s_i' -\delta_i \\ \Longleftrightarrow \forall i\in \{1,2,...,N\},P_{\pi(i)} = P_i' -\Delta_i f(z)=g(z)⟺i=1∑N​zπ(i)sπ(i)​=i=1∑N​zπ(i)(si′​−δi)⟺∀i∈{1,2,...,N},sπ(i)​=si′​−δi​⟺∀i∈{1,2,...,N},Pπ(i)​=Pi′​−Δi​
很明显z不能等于 0 或 1，当且仅当shuffle过程是有效的，多项式$f$和$g$相等

Checking the Polynomial Equality

为了检查多项式相等，我们计算这两个多项式在点 z c ← Z q \ { 0 , 1 } z_c \leftarrow Z_q \backslash \{0,1\} zc​←Zq​\{0,1}处的打开值，然后检查$f(z_c)=g(z_c)$，然而这不能保证这两个多项式完全相等，Schwartz-Zippel 定理告诉我们大概以$1-\frac{N}{Z_q}$的概率趋于相等，其中$|Z_q|>>N$.

其次，我们也不能直接计算这两个多项式，因为我们不可能获取到$s_{\pi (i)}、s_i^{\prime },{\delta }_i$这些秘密值，所以只能通过计算下面这个等式来验证：
$$\sum _{i=1}^N{z}_c^i{P}_i=\sum _{i=1}^N{z}_c^{\pi (i)}(P_i^{\prime }-{\Delta }_i)$$

Ensuring the Prover Behaves Honestly

如前面所说，等式右边（${\sum }_{i=1}^N{z}_c^{\pi (i)}(P_i^{\prime }-{\Delta }_i)$）只能由不受信任的证明者进行计算，且不泄露任何隐私信息。我们通过承诺(commitments)和零知识证明(zero-knowledge arguments)来满足这些属性。

首先，证明者会对置换进行承诺，并通过zero knowledge证明他们按照已承诺的置换对挑战$z_c$的幂进行了置换，最后验证者可以得到承$C_{z,\pi }$，其是对向量$[z_c^{\pi (1)},z_c^{\pi (2)},...,z_c^{\pi (N)}]$的承诺，这个向量可用于内积证明(inner-product argument)，以生成可证明的期望值:${\sum }_{i=1}^N{z}_c^{\pi (i)}(P_i^{\prime }-{\Delta }_i)$

这些arguments并不是平凡的(trivial)，可能需要单独的文章来提供数学方面的理解。此外在《Efficient Zero-knowledge Argument for Correctness of a Shuffle》中提到的 inner-product argument和permutation argument后来也分别被Bulletproofs和PlonK采用和改进。

From Shuffling Group Elements to Shuffling Cards

请注意，以上讨论仅涉及对单个群元素进行洗牌，而不是对一个掩码卡牌（由两个群元素组成的密文）进行洗牌。然而，我们可以将上述过程扩展到掩码卡牌，这里推荐两种方式：

1. 证明者分别在两组群元素上执行argument，同时要求证明对这两组元素使用相同的置换。这对于现有的argument structure是可行的，因为证明者已经承诺了一个置换并且证明了它的正确性。
2. 将每张掩码卡牌视为群$\mathbb{H}=G\times G$中的一个元素，并定义群$\mathbb{H}$的操作。